量子ゲートを描いて自動計算（Raspberry Pi+Mathematica）

2024年9月13日 12:46

100ページ目まで来ました。手で計算してましたが、そろそろ限界…
Mathematicaで出来ないですかね？
※その後、第3章を突破。機械的にPythonを写すんじゃないので、Mathematicaでの表現を考えるのでより理解が深まった気がします。Mathematicaの場合はToffoliの様な長いルーチンが省略して簡易表現されないので、横に延々と伸びてしまいます。学習には向いてますが、実際にはPythonの方がいいですね。

普通はPythonでやるのは分かってますよ。
私はPythonはあまり使いたくないのです。コードが10行超えるので。
Mathematicaなら5行、メイン部は1行。

PacletInstall["Wolfram/QuantumFramework"]
Needs["Wolfram`QuantumFramework`"]

👆ここ（2行目）でエラーを多量に吐きますが気にしない様に。

qc = QuantumCircuitOperator[{"H", "CNOT", {1}, {2}}];
qc["Diagram"]

Hをq[2]にしたい場合は　"H" ->2
CNotを逆向きにしたい場合は　"CNOT" -> {2, 1}

さぁ、問題は計算結果…　心配御無用。全然読めないけどこうします。

FullSimplify[#, Assumptions -> {0 <= p <= 1}] & /@ 
 qc[]["Probabilities"]

👆つまり、|00>を入れると、答えは(|00>+|11>)/√2に。

ヒストグラムはこう書きます。

qc[]["ProbabilityPlot"]

ちょっと長いのはこんな感じです。

qc = QuantumCircuitOperator[{"X" -> 2, "H", "H" -> 2, "CNOT", 
    "CNOT" -> {2, 1}, "CNOT", "H", "H" -> 2, {1}, {2}}];
qc["Diagram"]

👆つまり、|00>を入れると、答えは|10>に。

CNOTを途中に入れたい時は

qc = QuantumCircuitOperator[{"X", "X" -> 2, "X" -> 3, "X" -> 4, "H" -> 2, "CNOT", "H" -> 2, "H" -> 4, "CNOT" -> {3, 4}, "H" -> 4, {1}, {2}, {3}, {4}}];
qc["Diagram"]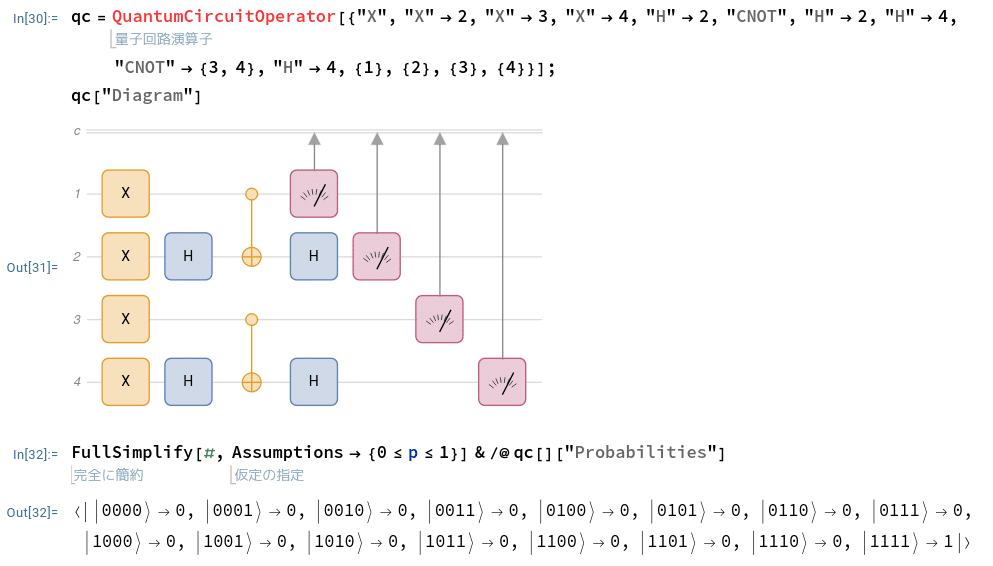

ユニタリー行列のUは無いみたいなので、こう？答えは合ってます…
ユニタリー回転ゲートはXYZ軸回転のSO(3)で正規化したものです。

qc = QuantumCircuitOperator[{"RX"[\[Pi]], "RZ"[\[Pi]], {1}}];
qc["Diagram"]

U1はRzで代用できる様です。

U1(λ) = Rz(λ)　　　　　　　
これはいいんですが

U2(φ, λ) = RZ(λ)→RY(φ)
角度の順を逆にして、Z→Yの順！

U3(θ, φ, λ) = RZ(λ)→RY(θ)→RZ(φ)
これは面倒。
まず3番目の　角度を最初に持ってきてZ回転
次に1番目の　角度を持ってきて　　　Y回転
最後に2番目の角度を持ってきて　　　Z回転

通常、XYZと書いてあったらZ→Y→Xの順に処理します。
Geminiは純粋に処理順でXYZと書いてくる様で、混乱しました。

†は意味が分からないのでGeminiに聞きました。
　S†はどうするのか？→Sゲートを2回掛ける
　T†はどうするのか？→Tゲートを2回掛けるとSゲートになり、
　　　　　　　　　　　 Tゲートを4回掛けるとT†ゲートになる。
MathematicaのQuantumCircuitOperatorは†（エルミート共役）は標準で無いみたいだけど、これでクリア？と思っていたら

S†とT†について、Claudeから面白い情報を得ます。
Pを使えるらしいですね。

らしいので、SとS†、TとT†はこれでいいのではないでしょうか？

qc = QuantumCircuitOperator[{"S", "P"[-\[Pi]/2] -> 1, "T", 
    "P"[-\[Pi]/4] -> 1, {1}, {2}}];
qc["Diagram"]

しかしToffoliを書いたらちゃんとT†が表示される…
どうやって書くのでしょうね？

qc = QuantumCircuitOperator[{"X", "X" -> 2, "Toffoli", {1}, {2}, {3}}];
qc["Diagram"]

順番が逆だけど、3年ぶり解説書を読んでみました。
読めるじゃない！いつの間に？
多分、リー群をやって量子ゲートの動きを勉強したからですが。

そうそう…
テンソル積も自分で計算するのが面倒くさいんですよ。
少し前まではMathematicaでは出来なかった…
今は出来るんです！

※この本はテンソルの扱いをゼロから作っちゃう試みだったですね。

◯まずは２次元

(*二つのベクトルのテンソル積*)v = {1, 2, 3};
w = {4, 5};
tensorProduct = Outer[Times, v, w];
(*行列形式で表示*)
MatrixForm[tensorProduct]

◯３次元

(*2つの正方行列を定義*)A = {{1, 2}, {3, 4}};
B = {{5, 6}, {7, 8}};
MatrixForm[A]
MatrixForm[B]
(*テンソル積を計算*)
tensorProduct = Outer[Times, A, B];
(*結果を表示*)
MatrixForm[tensorProduct]

◯４次元はもう手で計算したくないレベルです…

(*3つの3\[Times]3の正方行列を定義*)
AA = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
BB = {{10, 11, 12}, {13, 14, 15}, {16, 17, 18}};
CC = {{19, 20, 21}, {22, 23, 24}, {25, 26, 27}};
(*AとBのテンソル積を計算*)
tensorProductAB = Outer[Times, AA, BB];
(*A,B,Cの3つのテンソル積を計算*)
tensorProductABC = Outer[Times, AA, BB, CC];
MatrixForm[tensorProductABC[[1, 1]]]
MatrixForm[tensorProductABC[[1, 2]]]
MatrixForm[tensorProductABC[[2, 1]]]

公式参考URLは

慣れてくると、これくらいは1分で描けます。

量子ゲートを描いて自動計算（Raspberry Pi+Mathematica）

いいなと思ったら応援しよう！