
n=2の結果から考える~分散って何?
まずは復習から
前回、n=2のデータで、平均と分散と標準偏差を求めた。今回は、それをもう少し深めてみよう。まずは復習である。平均と標準偏差を求めてみよう。
データ1:{ 2, 6 }
データ2:{ 5, 9 }
データ1では、平均=4、分散=4、標準偏差=2になる。
データ2では、平均=7、分散=4、標準偏差=2になる。
問い
データ1とデータ2から考えよう。分散と標準偏差が、データ1とデータ2で同じになったのだが、これはどういうことだろう。データ1とデータ2には、同じ数値は含まれていない。平均も違う。なのに、分散と標準偏差を計算すると、どちらも、分散=4になる。(分散が同じなら、当然、その平方根である標準偏差も同じになる。)
これは、偶然に起きていることなのだろうか。それとも、データのある性質によって、必然的に起きていることなのだろうか。
少しだけ考えを巡らせてから、次に進もう。
(Thinking time …..)
重心としての平均
数直線のうえに、データ1をプロットする。青いひし形で示したのがデータだ。プロットを重り、数直線をてんびんに見立てて、ちょうど釣り合う位置を探す。ちょうど4の位置をささえてやると、てんびんは釣り合うはずだ。
こんなふうに、数直線上にデータをプロットしたとき、平均の値は、ちょうど「てんびんの重心」になる。今はデータが2個なのできわめてわかりやすい。データがいくら増えても考え方は同じである。

重心からの距離としての偏差
では、偏差はどのように考えられるだろうか。平均の位置に赤い★印をおいた。
(1)データ{2}の偏差は{ー2}だった。これは、「2」という数値が、平均の位置から、左へ「2」だけ離れていることを示している。
(2)データ{6}の偏差は{2}だった。これは、「6」という数値が、平均の位置から、右へ「2」だけ離れていることを示している。
マイナスとプラスの違いはあるけれど、どちらも「2」だけ離れている。これは偶然だろうか?
偶然ではない。片方が1離れていて、他方が3離れている位置に平均があったら、そもそもてんびんが釣り合わない。てんびんが釣り合う位置に平均を置いたのだから、データから平均までの距離は同じになるはずだ。

分散を求めるために、偏差を2乗する。どちらも4になる。足し合わせて2で割ったら4、平方根をとったら2である。
数値を変えても同じになるのは・・・
では、同じことを、データ2でもやってみよう。
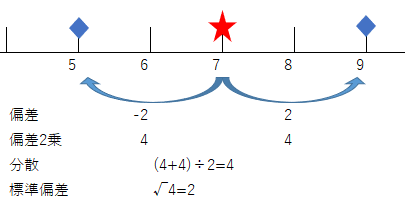
この図を見れば、データ1とデータ2とで、分散が(標準偏差も)同じになる理由がわかるだろう。たしかに数値は違っていたが、2つの数値が4だけ離れている、という性質は同じだった。だから、分散が(標準偏差も)同じになったのだ。
ここから、分散(標準偏差)についてとても大事なことが分かる。
分散や標準偏差は、データの数値たちが「お互い、どのくらい離れているのか」を表している。
(ただし、n=2の場合。n=3以上になると、基本的には同じように考えられるのだが、これほど単純な話にはならない。)
しつこく練習
もう一度、練習問題である。2つの数値がどのくらい離れているのか、そのとき分散や標準偏差はいくつになっているのかを、よくよく見ていただきたい。数値どうしの差が大きいほど、分散も標準偏差も大きな値になっているはずである。
データ3:{ 1, 7 }
データ4:{ 4, 16 }
データ5:{ 20, 100 }
データ6:{ 3450, 3450 }
数が大きくなるとちょっと心配になるかもしれないので、数行スクロールすると答えが見えるようにした。
答え↓
答え↓
答え↓
答え↓
答え↓
データ3:平均 4、分散 9、標準偏差 3
データ4:平均 10、分散 36、標準偏差 6
データ5:平均 60、分散 1600、標準偏差 40
データ6:平均 3450、分散 0、標準偏差 0
