
n=3で考える:気まぐれな3人目は平均値と標準偏差をどのくらい変化させるか
平均値と標準偏差の変化を可視化する
分散の変化をグラフにしてみる:n=2の場合で、分散や標準偏差は、データの数値たちが「お互い、どのくらい離れているのか」を表していることをグラフで可視化した。その記事の最後で、n=3だったらどうなるか? と書いたが、この記事がその答えになる。
気まぐれな3人目
何でもいいのだが、今の主観的な気分などを、3人の人に尋ねてみた、というような状況を考えよう。10点満点で、「これ以上ないくらい最悪=0、これ以上ないくらい最高=10」で点数をつけてもらう。1人目と2人目はそれぞれ、3点、7点を答えた。3点をつけた人には、「どうしたの?」と気にかけてあげたいが、残念ながら一人ずつカウンセリングをすることは調査の目的ではないので、とりあえず3人目にも答えてもらう。
ところが3人目は気まぐれで、最近のいろいろな出来事を突然思い出しては、「0点だ・・・」と言ったかと思えば「やっぱ10点!」と言い出したりする。困った回答者である。
そこで、何点と答えられても慌てないように、すべての場合について考えてみよう。という感じの状況設定である。(かなり無理ではある。)
計算してみた

表の構成はn=2とほぼ同じである。
x1~x3:それぞれ報告してもらった点数(0~10点)
median:中央値、mean:平均値、var:分散、sd:標準偏差
difab:xaとxbの得点差の絶対値。(dif12はx1とx2の差の絶対値)
dif.m:difabの平均値、dif2m:difabの2乗の平均値
注意:ここで計算しているdifab以下の指標は、n=2とのつながりを見ていくための指標である。つまり、「数値たちがお互いどのくらい離れているか」を数値化してみたものである。n=4になったときに、この指標がとても現実的には使えないことが判明するはずである。つまり、実際には統計処理ではこのような計算は行われない。
平均値と中央値

細い点線が3つの数値で、黄色実線が中央値、青実線が平均値である。平均値が、単純に、直線的に変化しているのに対して、中央値はそうではない。3人目が、他の2人の間の数値(3~7の範囲)を選んだ時、中央値は3人目の数値そのものになるが、それ以外の範囲では、ずっと一定になる。中央値の性質として、外れ値に対する頑健性(外れ値に影響されにくい性質)があるが、そのことがグラフからわかる。
分散と標準偏差

分散と標準偏差は、やはり2次曲線を描いて変化する。放物線の頂点は、x3=5のときである。つまり、3人の数値が{3,7,5}になったとき、分散と標準偏差は最も小さい値になる。では、このとき、「数値同士の距離」はどうなっているだろうか。
数値同士の距離

数値同士の距離を見てみよう。やや細い3本の破線がそれを示している。3つの「距離」の平均が、やや太い、青の破線で示されている。この折れ曲がり方を見て、どう思われるだろうか。どこかで見たような折れ曲がり方ではないだろうか。
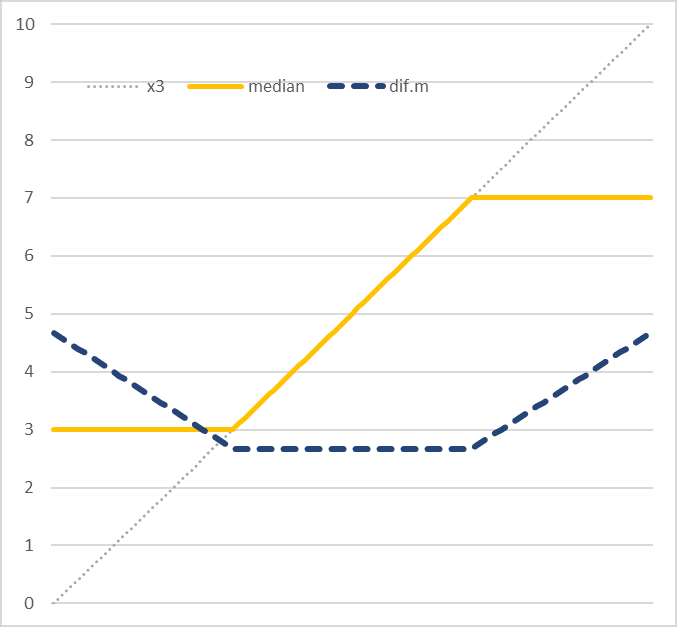
中央値の折れ曲がり方と似ている。折れ曲がり方の形状は異なるが、折れ曲がっているポイントが同じなのだ。数値同士の距離の平均が最も小さい値を示すのは、気まぐれな3人目が、他の2人の数値の間の数値であるときだ。言い換えると、データの「範囲」(=最大値-最小値)が、「7-3=4」で一定の間、数値同士の距離の平均も一定である。気まぐれな3人目がこの範囲を超える数値を答えたとき、言い換えれば、3人目によって範囲がより大きくなる時、数値同士の距離の平均も大きくなる。
標準偏差と数値同士の距離の平均

では、標準偏差と、数値同士の距離の平均とでは、どちらが、統計的な指標として妥当だろうか。
n=2のとき、意味の分かりやすいのは、数値同士の距離だった。2つの数値同士の距離は、きれいにV字型を描いていた。しかし、n=3では、気まぐれな3人目が多少数値を変えても、それがある範囲(3~7)であれば、数値同士の距離の平均は一定だった。それが、グラフの中央部に表れている。
一方、標準偏差は、そのような3人目の気まぐれにもちゃんと反応している。3人目が「5」と答えた瞬間に最小の値を示し、そこから少しずれた数値を答えると、少しだけ標準偏差は大きくなっていく。
このように、1つ1つの数値の変化に敏感に反応して、2次曲線を描いて変化するのが、分散や標準偏差の特徴である。偏差を二乗する、という手間のかかる(初学者にとっては意味不明だったりする)計算をするのは、分散や標準偏差が、1つ1つの数値の変化に敏感に反応して、2次曲線を描いてほしいからである。
平均値、分散、標準偏差は、すべての数値を使って計算されるため、外れ値があると値が変化しやすい。そのことが、これらの統計量の欠点であるかのように、最初の内は理解してしまうかもしれない。しかし、それは違う。
1つ1つの数値に敏感に反応するからこそ、グラフにあるような放物線を描いて変化するのが、分散や標準偏差という統計量である。1つ1つの数値を一つも見捨てることなく、それぞれに評価していることが、これらの統計量の長所なのだ。
