
HADを使ってみた:平均値の比較におけるr効果量について
統計法で,r といったら,ピアソンの積率相関係数がぱっと頭に浮かびますね。2つの量的変数があって,一方が変化するともう一方も変化する,そこに直線的な関係,つまり一次関数的な関係がみられるかどうかを判断する基準になります。HADでは「散布図」や「相関分析」でこれを出力できますし,係数だけでいいなら,Excelの correl 関数でも出力できます。しかし,平均値の差の検定での r 効果量は,これとはちょっと意味合いが異なる(らしい)のですね。どういうことでしょうか。
対応のないt検定の場合
この前から使っている,森・吉田(1990)の例題を使って考えます。4水準のデータなのですが,第1水準と第2水準だけを使って,まず対応のないt検定をしてみましょう。データと出力はこうなります。
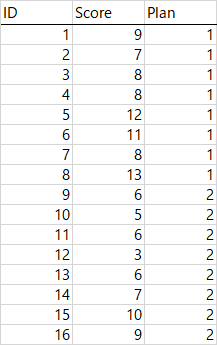
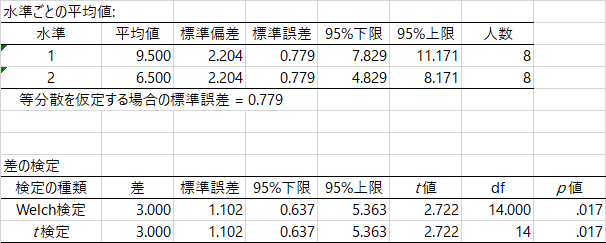
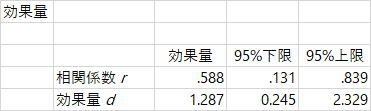
r 効果量にだけ注目すると,係数は .588 です。この値は何を意味するのでしょう。あるいは,どうやって計算するのでしょう。はじめに,以前にも引用した水本・竹内(2008)を見てみましょう。計算式とともに,次の解説があります。
ここで求められるrは,たとえば,実験群と統制群の2つのグループの点数を並べたものの相関係数ではなく,実験群と統制群のグループを表す名義尺度(0を実験群とし,1を統制群とするような2値データ)と点数の間の点双列相関係数である(水本・竹内(2008)p.61)
続いて,分散分析のη2乗効果量について説明があり,その中で,
t検定の効果量として説明したrは相関比の特殊な形である
とも説明されています。
相関比
「相関比」は聞きなれない用語ですが,森・吉田(1990)によれば,「R2が予測における分散説明率を表すことと同じ考え方に基づいて定義」される値であり,「一方の変数の尺度水準を名義尺度に落として2変数間の関係について検討するもの」(p.229)としています。算出方法は,
1:一方の変数をいくつかの段階(群)に分けてそれを独立変数とする。
2:他方の変数(y)を従属変数とする。
3:全変動,要因による変動,誤差変動を算出する。
4:相関比ηは,(要因による変動/全変動)の平方根で算出される。
なるほど,これなら知っています。分散分析の効果量を求めるときにこの手順でやりました。2要因以上のときは,「全変動」ではなく,「要因による変動+残差変動」で割って,偏η2として算出するのでした。
点双列相関係数
これも耳慣れない用語ですが,相関比の説明のすぐ後に,
相関比は,一方の変数がもともとカテゴリカルな変数で,他方が間隔尺度または比率尺度の変数である時の,2変数間の関係の強度を表す指標としても使われる。ただし,カテゴリカルな変数の水準が2である場合には,それぞれのカテゴリーに異なる数値(通常1と0)を代入してピアソンの積率相関係数を計算すれば,このような場合に適用される相関係数である点双列相関係数(point biserial correlation coefficient)を算出したことになる。
なるほど,よくわかりました。水本・竹内(2008)と同じ内容が書かれています。(当然か。)では,HADにその計算をやってもらいましょう。変数の設定はそのままで,散布図を描けば,点双列相関係数が算出できるはずです。結果はこんな感じ。
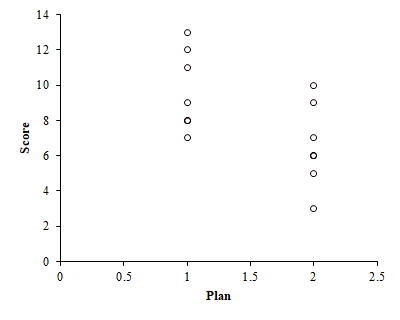
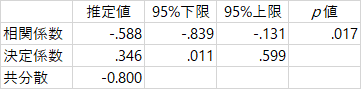
おお,プロットを見ると納得しますね。たしかに点が2列(双列)になっています。数値は .588 で,信頼区間も,さきほどのt検定のr効果量と一致しています。
分散分析で確かめてみる
ところで,この .588 という r 効果量の値は,相関比((要因変動/全変動)の平方根)と一致するそうですから,分散分析をして確かめてみましょう。といっても,HADでは2水準の分散分析をやってくれませんから(裏技があるんだろうか?),Excelに手伝ってもらって,手計算します。計算手順は統計法の教科書にゆずって結果だけ出しますと,こんな感じです。一致しました。
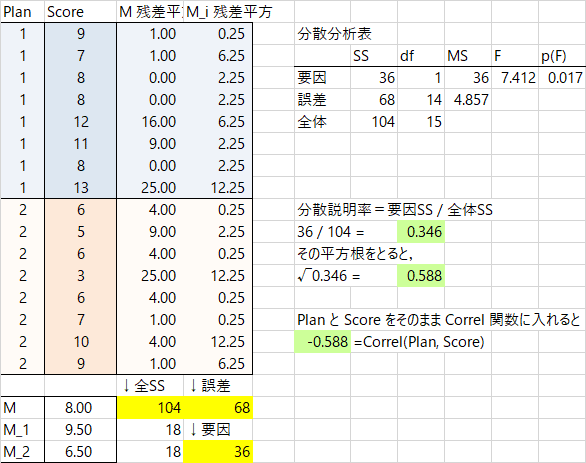
ということで,ひとまず解決しましたね。さきほどの点双列相関係数のプロットがわかりやすいと思います。この係数が大きいということは,2つの点双列の位置のずれが大きいことを意味しますから,水準間の平均値差もそれだけ大きく,有意になりやすいと考えられます。
対応のあるt検定
さてと。
問題は対応のある検定の方です。同じデータを使いますが,対応のあるデータという仮定のもとで検定してみましょう。結果はこうなります。
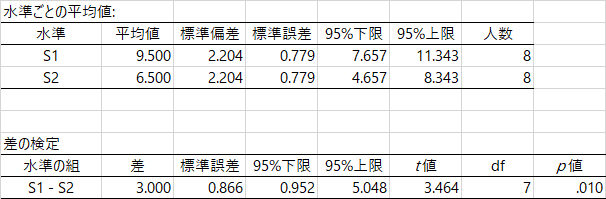
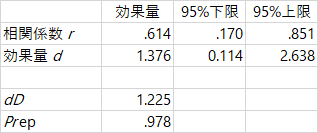
データは変わらないのに,対応のあるデータとして検定すると,やや大きいt値が得られます。r効果量もd効果量も少しだけ大きい値になっています。このことには,特に違和感はないのです。しかし,なぜかこのr効果量の値(.614)が計算できません。
まず,先ほどと同じように点双列相関係数を計算すれば,0.588になります。同じデータですから当然ですね。相関比も,対応のある検定ではWITHINの分散が入ってくる分,残差分散は小さくなりますが,要因による変動は同じです。同じでないとおかしいですね。ですから,(要因による変動/全変動)の平方根でもやはり0.588です。ならば,(要因による変動/要因による変動+残差変動)の平方根ということでしょうか。これは計算すると 0.795 になります。
対応のある検定は対応のない検定と何が違うかと言うと,2つのデータにつながりがあることです。つまり個人内の「値の変化」に注目するための検定でした。ならば,Score の得点差を用いて,点双列相関係数を算出すればいいのでしょうか。やってみましょう。
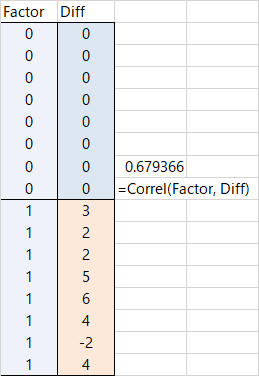
これだと,r = 0.679 になります。違うようです。
ということで,行き詰まっています。というのが,この note の結論でした!(笑)ついでに書くと,d 効果量も,対応のある検定の方は計算できません!(笑)さっき図で出した,2水準の差(Diff)の平均値と標準偏差を使った効果量は計算できてて,これはHAD出力の「dD」の値と一致します。ああ,「dD」って,「Difference」 を使った「d効果量」のことだったのか? などと,呑気な感動を味わったりしているのです。(笑)
タイトル画像
今回も下記のサイトから。検索ワードは「bored」でした。使ったのはPhoto by Colin Osborne on Unsplash。「わかんねえ・・・」って感じがとってもよく出ていると思いますが・・・
