
ジニ係数の計算
芳沢(2014)に、ジニ係数の計算が紹介されているので、より一般的な式に直して、ここにも書き残しておくことにしよう。といっても、だれかがもっとちゃんとやっているんだろうけど。自分の学習の記録として。
以下、第8章第2節 「確率と統計」に書かれていることの紹介である。
ジニ係数
本書には、簡単なデータによるジニ係数の導出、計算式の紹介がある。
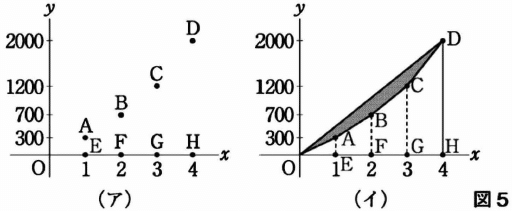
図の(イ)で塗りつぶされた部分の面積の、三角形ODHに対する割合がジニ係数である。以下、データ点(図中のA~D)を$${x_i}$$として記号の式で計算式を再現する。
(1)三角形ODH(底辺×高さ÷2):$${(x_1+x_2+x_3+x_4)\times 4 \times\frac12}$$
(2)三角形OAE(同):$${(x_1)\times 1\times \frac12}$$
(3)台形AEFB((上底+下底)×高さ÷2):$${(x_1+x_1+x_2)\times 1 \times \frac12}$$
(4)台形BFGC(同):$${(x_1+x_2+x_1+x_2+x_3)\times 1 \times \frac12}$$
(5)台形CGHD(同):$${(x_1+x_2+x_3+x_1+x_2+x_3+x_4)\times 1 \times \frac12}$$
(6)(2~5)の合計=塗りつぶされた部分より下:$${(7x_1+5x_2+3x_3+x_4)\times\frac12}$$
(7)塗りつぶされた部分=(1-6):
$${\Big\{(4x_1+4x_2+4x_3+4x_4)-(7x_1+5x_2+3x_3+x_4)\Big\}\times\frac12\\=(3x_4+x_3-x_2-3x_1)\times \frac12}$$
ここで、(7)式の結果のカッコ内は、4つのデータ同士の差の合計である。
(8)4つのデータ同士の差の合計は次のように求められる。ただし、$${x_i}$$は昇順にソートされていると仮定する。
$$
\begin{aligned} (D-C)&:x_4&-x_3\\ (D-B)&:x_4&&-x_2\\ (D-A)&:x_4&&&-x_1\\ (C-B)&:&x_3-&x_2\\ (C-A)&:&x_3&&-x_1\\ (B-A)&:&&x_2&-x_1 \end{aligned}
$$
これらを合計すると、$${3x_4+x_3-x_2-3x_1}$$となる。これを2で割ったものが、図5の塗りつぶされた部分の面積($${s}$$とする)と一致する。また、この計算は一般的に次のように表される。
$$
s=\sum_{i=1}^n (2i-1-n)x_i
$$
(9)(1)を次のように変形する。$${(x_1+x_2+x_3+x_4)\times 4 \times\frac12=\sum x_i\times n\times\frac12}$$ 。さらに、$${=\frac n2\sum x_i=\frac n2 \times n \times \bar x=\frac12 n^2\bar x}$$となる。
(10)(7)を、(8)を用いて次のように変形する。$${(3x_4+x_3-x_2-3x_1)\times \frac12=\frac12 s}$$
(11)(10÷9)が求めるジニ係数である。
$$
\frac12s \div \frac12n^2\bar x=\frac{s}{n^2\bar x}=\frac{\sum_{i=1}^n (2i-1-n)x_i}{n^2\bar x}
$$
間違っているよ!という部分を見つけた方は、どうぞ教えてくださいませ。
スクリプトも書けそうだから、そのうちやってみよう。
