解説　Tapa-Like Loop1(アゼン)

2021年4月28日 00:51

今日はこの問題を解説していこうと思います

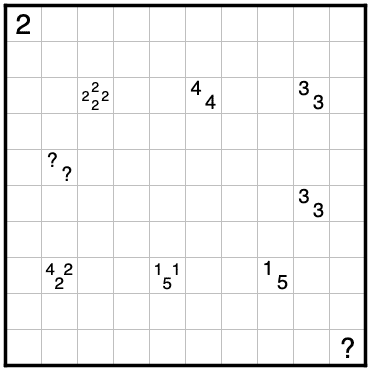
この問題のテーマは、前半は一部分だけ確定する線分、後半は偶数端点法です。

例えば、左上の2222はこのように決まります。

これは線の通り方について考えると簡単ですね

シンプルループなどでよく使う考え方ですが、一つのマスに注目したとき、線の出入り口の選び方は、図のように一つが壁になっているときは3通りとなります。

これはつまり線が通らない出入り口一箇所を決めているのとおなじですね。ここで2222の場合では、真ん中の配置があり得ないので、左右のどちらかになります。つまり壁の反対側から線が伸びることが明らかになります。

とこのように、"いずれにしろ"の考え方を利用することで線が確定していきます。今回の問題の前半はそれを利用していきます。

すると、ここまでは決まります。

次に1の数字について考えてあげると、下図のようになります。

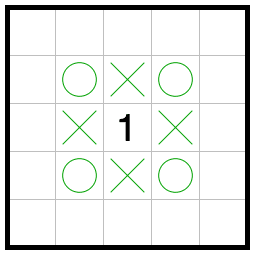
つまり、角にしか1の数字は存在することができないんですね。これについては少し考えてあげるとわかると思います。

つまり問題真ん中下の115の左に出た数字は5が回収しなければなりません。

ここでさらに5の数字について考えると、これは必ず入ったマスと反対のマスから出ます。つまり、こういうことです。

これもすこし考えてあげるとわかると思います。ということで問題はつぎのように進みます。

右下も同様に線が引けます。次に右下の15で5の取り方と1の場所が上の33によって確定します。

これを進めると

こうなりました。左下は偶端をつかうことで決まります。

ここからが難しい偶端です。上の空間に注目します。

ここで赤線部の左からからは1本しか線画でないことがわかります。

考えられるのは、0,1,2本ですが、0だと小ループ禁が起こり、2本だと、左上角の2の数字の条件を満たせないからです。

ここでさらに44の隣からは一本しか線が出ないことがわかります。つまりこうです。

つまり?は1本なので、そこを線が通ることがわかりました。

これを進めると

より、解けました。

要は44などの数字は偶端と相性がいいってことですね、たとえば下図のように決まります。

などのように決めさせることもできます。

おしまい