高校数学 三角比(三角関数) #12

リュディアです。引き続き三角比(三角関数)について見てみます。最後に三角形の面積についてまとめてみます。三角比(三角関数)は名前の通り三角形に絡めた問題が多く、特に面積を求める問題が多いです。公式の整理もしておきたいと思います。いつもの通り、標準的な三角形として次の三角形を考えます。

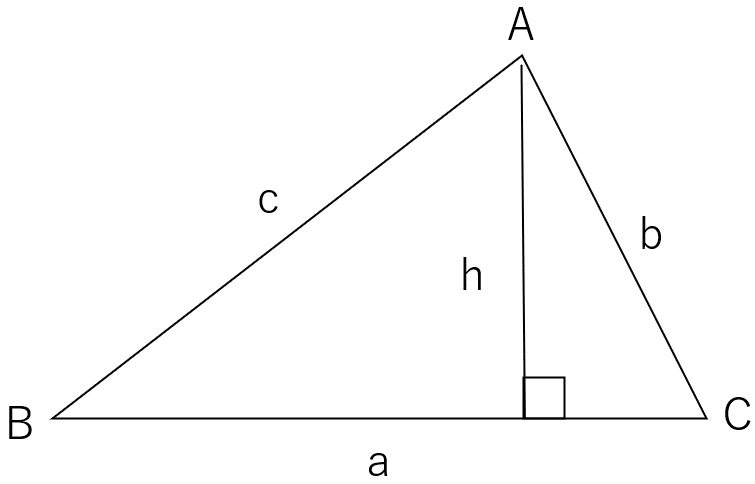
最も基本的な三角形の面積の求め方は底辺 x 高さ ÷ 2 ですね。図中の文字と合わせると次のようになります。

この図で皆さんは h を c と角Bで表現できることはわかりますね？

この式を面積の式に代入すると三角比（三角関数）で公式として学んだ三角形の面積の式になります。

次に正弦定理を考えます。三角形ABCとその外接円を考え、外接円の半径をRとします。

では正弦定理を書いてみてください。覚えてますか？

この式から sin Bの式を作ると次のようになります。

これを面積の式の sin Bに代入すると次のようになります。学校や先生によってはこれも公式として暗記させることもあるようです。私のおすすめは、こういう公式もあったな、とぼんやり頭にいれておいて、その場で作ること。時間がないといっても理解できていればせいぜい5-10秒程度です。

正弦定理で外接円が出てきたので次は内接円も考えてみましょう。一般的な三角形とその内接円の半径をr とします。

内接円の半径 rを使って三角形の面積を求めてみましょう。次の図の補助線を入れると簡単ですね。3つの三角形にわけて考えます。

内接円の中心と三角形の辺と接する部分は垂直に交わるので内接円の半径rが三角形の高さになることに気づけばすぐに求まります。この式は面積を求める式としてよりも内接円の半径 r を求める式として使われることも多いので次のように変形した式もぼんやりとでいいので頭においといてください。

そして最後がヘロンの公式です。中学でもやりましたね。何でもこの公式を使う人もいるのですが私はお勧めしません。そもそもこの公式の利用を想定して問題を作る先生も少ないですし、計算がごっつくなるので知識としては知っておけばよいですが最後の手段です。

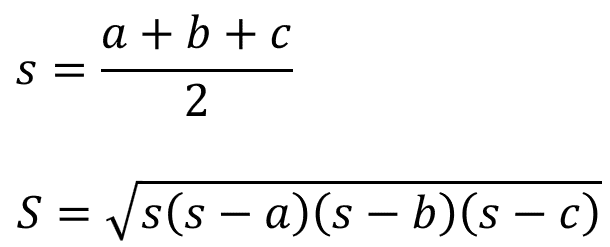
3辺が与えられて、ヘロンの公式を使いそうになっても、他の方法があるはず、と考えて最後の手段としてください。ポイントとしては sの値がシンプルになるときだけ使ってください。それ以外は使用禁止のつもりでよいと思います。

これでいったん三角比（三角関数）のまとめを終わります。一部、三角関数の範囲に入りましたが基本は三角比の部分のみです。ここでつまづくと三年で出てくる三角関数は確実にわからないです。基本なのでしっかりと身につけてください。

では、ごきげんよう。