高校数学 三角比(三角関数) #8

リュディアです。引き続き三角比(三角関数)について見てみます。今回は用語についてです。sin のことを正弦、cosのことを余弦、tan のことを正接とも言うことを聞いたことがあるかもしれません。雑学っぽいですがなぜ、そのように呼ぶのかまとめておきます。丸暗記で構わないのですがちょっとした知識があれば覚えやすくなりますから一読ください。次の図を見てください。

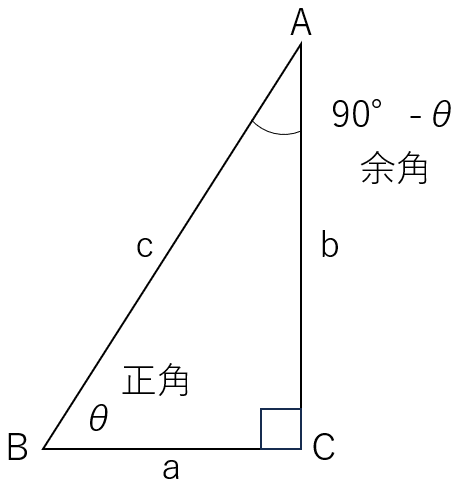
皆さんは正角（せいかく）、余角（よかく）という言葉をご存じですか？直角三角形を上の向きに配置したときに左下の角を正角、上の角を余角といいます。次にこの三角形に対して外接円を書きます。辺ABが直径になるような外接円になりますね。

ここで辺c、つまり円の直径を 1 とします。すると辺a, b の長さは次のようになります。緑色の字を見てください。

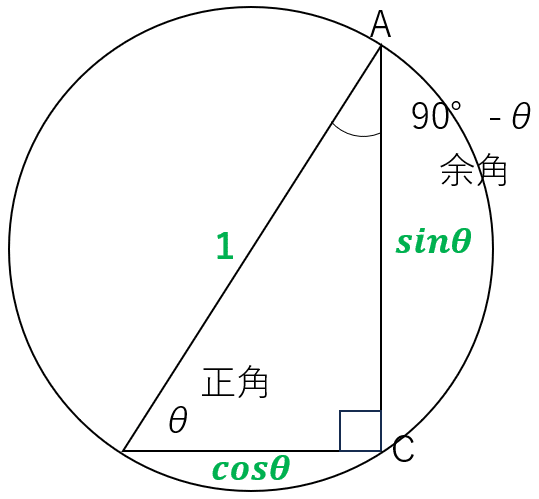
このとき正角とsinθ、余角とcosθの位置関係はどうなっているか見てみましょう。

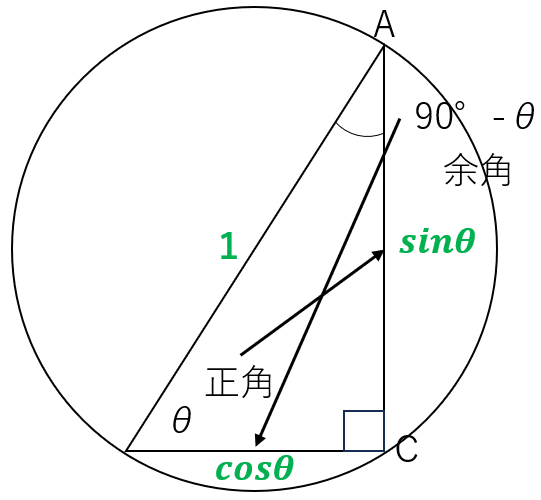
そう、それぞれ向かい合う関係ですね。つまり正角に対する円の弦がsinθ、余角に対する円の弦がcosθになっていますね。正角に対する弦の長さがsinθなのでsinθを正弦、余角に対する弦の長さがcosθなのでcosθを余弦と呼びます。

最後に tan も観てみます。三角形の頂点Aにおける円の接線を引き、その延長と三角形の辺a の延長が交わる点を Pとします。

このときtanθは図中の緑線部、つまり辺APとして表現できます。つまり正角に対する円の接線ということで正接と呼びます。これは少し強引な気が。。。

今回は正弦、余弦、正接という名前付けの由来をまとめてみました。たまに正弦が sin なのか cos なのかわからない、という方もいます。確かにこれは覚えるしかないのですけど、それでも何か根拠になることを知っていれば単に丸暗記するよりは頭に残りやすいと思います。

では、ごきげんよう。