高校数学 三角比(三角関数) #10
リュディアです。引き続き三角比(三角関数)について見てみます。今回は余弦定理です。余弦と名がついているので cos に関する定理のようですね。正弦定理に匹敵する重要な定理ですのでしっかりと理解してください。まず余弦定理を見てください。

なんだか項数も多いし複雑そうな式ですね。三角形の3つの辺の長さと1つの角の余弦の大きさの関係を示しています。証明とまではいきませんが簡単な導出をしてみます。次の三角形を見てください。

一般的な三角形です。直角もありません。この三角形にAから対辺に垂線をおろし、交点をDとします。次のようになります。
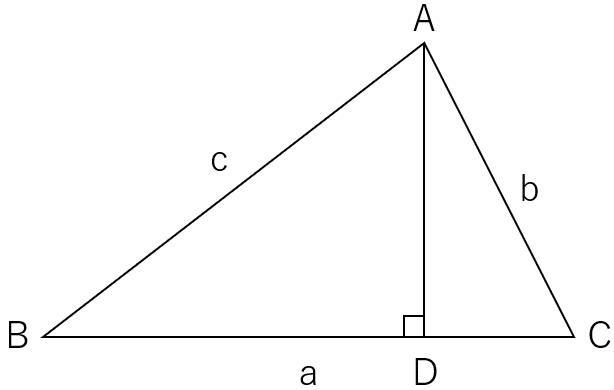
ここで右側の直角三角形に注目してbと角Cを使って辺AD、辺CDの長さを求めると次のようになります。

次に左の直角三角形に注目して辺BDを求めます。

そして左の直角三角形で三平方の定理を使って式の間の関係を記述して変形します。
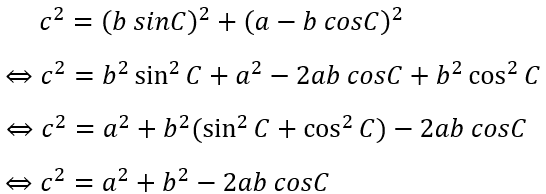
余弦定理の式が出てきましたね。これは導出なので覚える必要はないのですが一度は手を動かして計算してみてください。余弦定理は式が複雑なのですが落ち着いてみると癖というか対応関係があることに気づきます
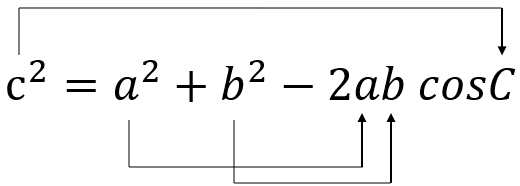
マイナスの符号は注意が必要ですが、このように見てみるとサイクルがあるように感じませんか?また三平方の定理から導出していることから最後の項を別にすれば三平方の定理なわけです。直角三角形であれば三平方の定例が成り立つ、しかし直角三角形ではないから補正項が必要で、それが -2ab cosC であると考えれば少しでも覚えやすいと思うのですがいかがでしょうか。再度、自分で手を動かして覚えてください。
では、ごきげんよう。
