高校物理 定滑車と2つの物体のつり合いと等加速度運動 #1

リュディアです。先日、親戚の高校生から物理の問題の質問を受けました。久しぶりだったのですが、確かに自分も混乱した記憶があるなと思いましたので、高校生に教えながら考えたポイントなどをまとめておきたいと思います。問題も手元にあるのですが著作権やらにあたると嫌なので自分で絵も書いて記号も変更しています。

まず次のような設定の問題です。図と設定を見てください。問題は大きく前半、後半にわかれておりこれは前半の設定です。

まず最初に気づかないとダメなのはすべての物体が静止している、つまりつり合いの関係にあるということです。つり合いの関係が成立するのは静止しているか、等速直線運動のときでしたね。覚えていますか。今回は静止していますので各物体にかかる力の間につり合いの関係が成り立ちます。順に見ていきましょう。まずは物体Aにかかる力です。

物体Aにかかる力は重量と張力のみです。下向きを正とすると次のようなつり合いの式から張力T1を求めることができます。

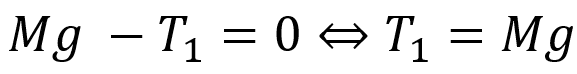
同様に物体Bについても見てみましょう。今度は物体Bにかかる力とつり合いの式をまとめて記載します。

物体Bにかかる力は重量と2つの張力です。下向きを正とすると図中にあるようなつり合いの式が成り立ち張力T3を求めることができます。

最後に定滑車についても見てみましょう。定滑車にかかる力とつり合いの式をまとめて記載します。

定滑車にかかる力は重量と1つの上向きの張力、2つの下向きの張力です。問題の設定で定滑車自身の質量は0なので重力はゼロとなり、1つの上向きの張力、2つの下向きの張力が釣り合う関係になります。

これでT1, T2, T3が求まりました。実はこの問題の前半はすべての物体が静止している状態での糸1, 2, 3 の張力を求めよというものです。いずれも簡単ですね。しかし定滑車にかかる力を理解できていない人もいるかもしれません。定滑車にかかる力を整理しておきましょう。定滑車の両側に同じ質量の物質A, B をつりさげ、静止状態つまりつり合いの状態にあるとすると以下のようになります。

この図で関係が理解できますか？つり合いと作用反作用の関係が混乱している人も多いのでこのタイミングでしっかりと理解してください。

では次回につながる話をして終わりにしたいと思います。皆さんは運動方程式をご存じだと思います。力の合計が質量と加速度の積になるという有名な方程式です。高校では加速度 aとして次のように書くことが多いですね。

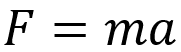
これは物体のいろいろな運動を表現できるのですが、ここで加速度 a = 0 、つまり静止しているか等速直線運動をしている場合にこの式はどうなりますか？もうわかりますね。

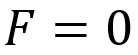
これはつり合いの式ですね。つまり運動方程式で加速度が0の場合につり合いの式になるというわけです。今回は物体が静止している、つまりつり合いの関係を利用して解く問題でした。次回は運動方程式を使うパタンを扱います。

では、ごきげんよう。