高校生のための加法定理
みんな大好き加法定理。
$$
\sin(\alpha +\beta)=\sin{\alpha}\cos \beta +\cos \alpha \sin \beta \\
\cos(\alpha +\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta
$$
ここでは、証明には一切触れることなく、関連するトピックについて自由闊達に書いてみようと思います。
倍角や半角
まず、ウォーミングアップとして、倍角の公式を見ていこう。
加法定理に対して、$${\alpha =\beta}$$としてあげれば、
$$
\sin 2\alpha =2\sin \alpha \cos \alpha \\
\cos 2\alpha =\cos^2\alpha -\sin^2 \alpha
$$
となります。$${\cos}$$のほうで、$${\sin}$$だけ、あるいは$${\cos}$$だけにあわせると、$${\sin^2\theta +\cos^2 \theta =1}$$であるから、
$$
\cos 2\alpha =2\cos^2\alpha -1 \\
=1-2\sin^2\alpha
$$
であるとわかります。
半角に関しては、
$${\alpha}$$を$${\frac{\alpha}{2}}$$とすれば
$$
\cos ^2 \frac{\alpha}{2}=\frac{1+\cos \alpha}{2} \\
\sin ^2 \frac{\alpha}{2} =\frac{1-\cos \alpha}{2}
$$
をえることができます。
和積や積和
以下の「公式」は覚えるものではないといわれることもあるでしょう。
加法定理を並べて考えれば、すぐに導けるもので、中身はほとんど加法定理です(?)
では、足したのと引いたのを並べましょう。
$$
\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\
\sin (\alpha -\beta)=\sin \alpha \cos \alpha -\cos \alpha \sin \beta
$$
辺々加えれば、
$$
\sin (\alpha +\beta)+\sin (\alpha -\beta )=2\sin \alpha \cos \beta
$$
したがって、
$$
\sin \alpha \cos \beta =\frac{1}{2}\{\sin(\alpha +\beta)+\sin (\alpha -\beta)\}
$$
またここで$${A=\alpha +\beta,B=\alpha -\beta}$$とすると、
$${\alpha =\frac{A+B}{2},\beta =\frac{A-B}{2}}$$であるから、
$$
\sin A +\sin B =2\sin \frac{A+B}{2}\cos \frac{A-B}{2}
$$
まったく同じように、他の「公式」も導くことができます。
例えば、$${\cos}$$と$${\cos}$$の積を足し算にしたいと思えば、$${\cos \alpha \cos \beta}$$を含む、$${\cos}$$の加法定理を用いれば、
$$
\cos (\alpha+\beta)=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\
\cos (\alpha -\beta)=\cos \alpha \cos \beta +\sin \alpha \sin \beta
$$
の辺々を加えて、
$$
\cos(\alpha +\beta)+\cos (\alpha -\beta)=2\cos \alpha \cos \beta
$$
より、$${2}$$で割って、$${\cos \alpha \cos \beta =\frac{1}{2}\{\cos(\alpha +\beta)+\cos (\alpha -\beta)\}}$$をえることができます。
複素数の積~回転~
複素数の掛け算は複素平面での回転を表します。
極形式で考え、簡単のために大きさを$${1}$$にします:$${r=1}$$
二つの複素数$${z_1,z_2}$$を考えましょう。これを極形式で表すと、
$$
z_1=\cos \theta _1+i\sin \theta _1 \\
z_2=\cos \theta _2 +i\sin \theta _2
$$
積$${z_1z_2}$$を計算してみると、
$$
z_1z_2
=(\cos \theta _1+i\sin \theta _1)(\cos \theta _1+i\sin \theta _2) \\
=(\cos \theta _1\cos \theta_2 -\sin \theta _1\sin \theta _2)+
i(\cos \theta _1\sin \theta _2 +\sin \theta _1 \cos \theta _2) \\
=\cos (\theta _1+\theta _2)+i\sin (\theta _1+\theta _2)
$$
となります。
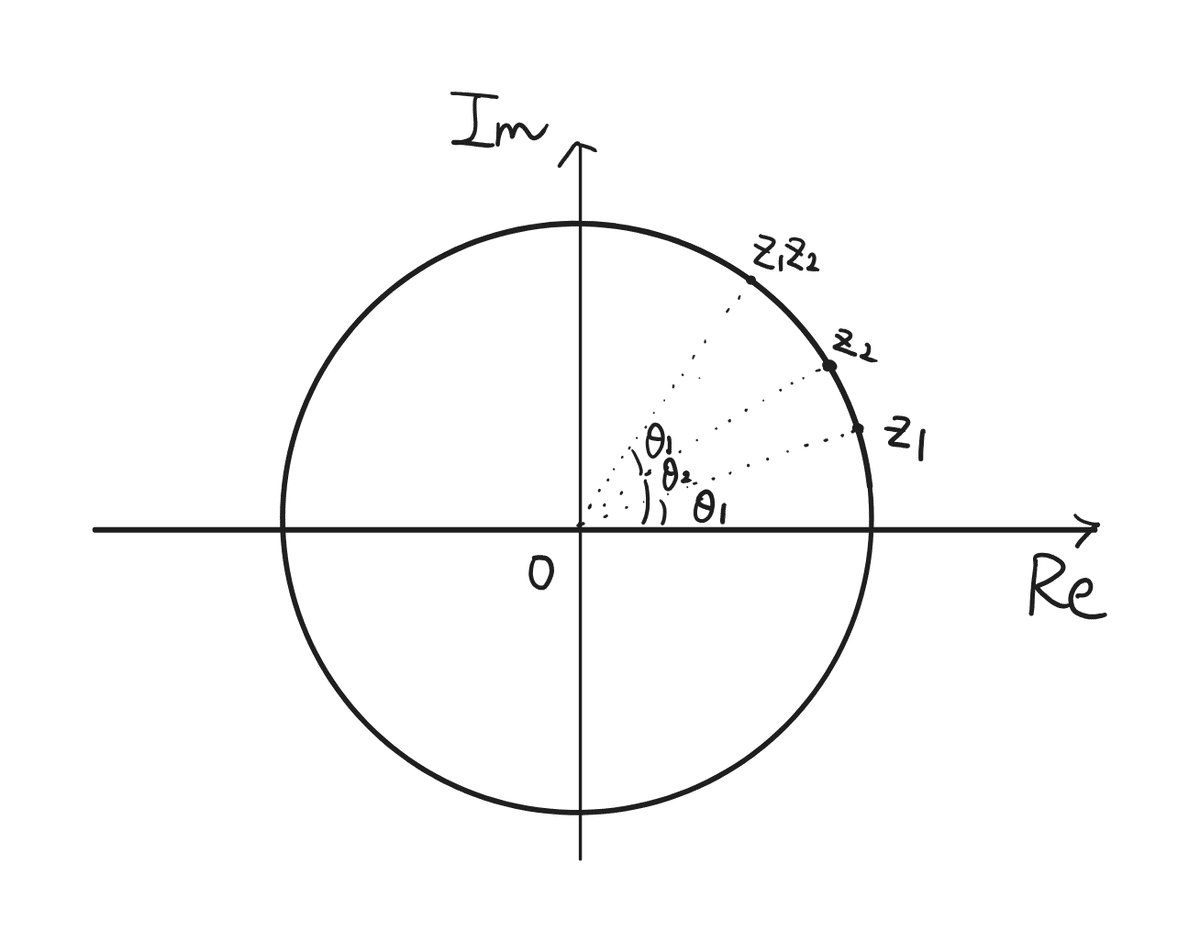
複素数の積は「大きさ(絶対値)は掛け算、角度(偏角)は足し算」になります。
行列で回転を表すこともできます。
雑に触れてみましょう。
平面($${\mathbb{R}^2}$$)と複素数(複素数全体$${\mathbb{C}}$$)を同一視します:つまり$${(x,y)}$$と$${x+iy}$$を同じものと考えます。
さっきの計算から、
$$
\begin{pmatrix}
\cos (\theta _1+\theta _2)\\
\sin (\theta _1 +\theta _1)
\end{pmatrix}
=\begin{pmatrix}
\cos \theta _2 & -\sin \theta _2 \\
\sin \theta _2 & \cos \theta _2
\end{pmatrix}
\begin{pmatrix}
\cos \theta _1 \\
\sin \theta _2
\end{pmatrix}
$$
これより、
$$
\begin{pmatrix}
\cos \theta _2 & -\sin \theta _2 \\
\sin \theta _2 & \cos \theta _2
\end{pmatrix}
$$
をかけることで$${\theta _2}$$回転します。
オイラーの公式
$$
e^{i\theta}=\cos \theta +i\sin \theta
$$
この式の証明などの説明は一切せず、認めることにします。
加法定理は指数法則として捉えることができます。
さきほどの単位円周上の二点$${z_1,z_2}$$をとってきます。
このとき
$$
z_1=e^{i\theta _1} \\
z_2 =e^{i\theta _2}
$$
であるから、その積$${z_1z_2}$$は
$$
e^{i\theta _1}e^{i\theta _2}=e^{i(\theta _1+\theta _2)}
$$
となり、$${\sin ,\cos}$$になおして、実部と虚部を比較すれば、加法定理の形を得ることができます。
微分
$${\sin}$$の微分を求めましょう。
定義にしたがって極限
$$
\lim_{h\to 0}\frac{\sin (x+h)-\sin x}{h}
$$
を計算します。加法定理でばらすと、
$$
\frac{\sin (x+h)-\sin x}{h} \\
=\frac{1}{h}(\sin x\cos h +\cos x \sin h -\sin x) \\
=\sin x \frac{\cos h -1}{h}+\cos x\frac{ \sin h}{h}
$$
いま、
$$
\lim_{h\to 0}\frac{\sin h}{h}=1 \\
$$
であり、
$$
\lim_{h\to 0} \frac{\cos h -1}{h} \\
=\lim_{h\to 0} \frac{\sin^2 h}{h(\cos h +1)} \\
=\lim_{h\to 0} \frac{\sin h}{h}\cdot \frac{\sin h}{\cos h +1}\\
=1\cdot \frac{0}{2} =0
$$
よって、この極限値は$${\cos x}$$である。
$$
\frac{d}{dx}\sin x=\cos x
$$
こうして、お馴染みの結果を得ることができました。
これは和積をつかって計算することもできます。
$${\sin}$$の加法定理で引き算を考えてやればよく、極限の中身$${\sin (x+h)-\sin x}$$は
$$
\frac{1}{h}2\cos (x+\frac{h}{2})\sin \frac{h}{2} \\
=\cos (x+\frac{h}{2})\frac{\sin \frac{h}{2}}{\frac{h}{2}}
$$
から上と同じ結果を得られます。
t=tan(x/2)
$${t=\tan \frac{x}{2}}$$は置換積分でよくみるでしょうか。被積分関数の三角関数を有利関数にすることができます。まず、$${\tan x}$$を$${t}$$で表してみましょう。
$$
\tan 2x=\frac{\sin 2x}{\cos 2x} \\
=\frac{2\sin x\cos x}{\cos^2 x -\sin^2x} \\
=\frac{2\frac{\sin x}{\cos x}}{1-\frac{\sin^2x}{\cos^2x}} \\
\frac{2\tan x}{1-\tan^2x}
$$
であるから、$${x}$$を$${\frac{x}{2}}$$と考えれば、$${\tan x=\frac{2\tan x/2}{1-\tan^2 x/2}}$$とわかるので、
$$
\tan x=\frac{2t}{1-t^2}
$$
では、次に$${\cos}$$を$${t}$$で表しましょう。
$${\sin^2\theta +\cos^2 \theta =1}$$の両辺を$${\cos^2 \theta}$$で割ると、$${\tan^2 \theta +1=\frac{1}{\cos^2x}}$$であるから、
$$
\cos^2x=\frac{1}{\tan^2 x +1} \\
=\frac{1}{(\frac{2t}{1-t^2})^2+1}\\
=\frac{(1-t)^2}{(1+t)^2}
$$
ここで$${\cos x>0}$$とすると、
$$
\cos x=\frac{1-t}{1+t}
$$
を得ます。さらに$${\sin x=\tan x \cos x}$$より、
$$
\sin x
=\frac{2t}{1-t^2}\cdot \frac{1-t^2}{1+t^2} \\
=\frac{2t}{1+t^2}
$$
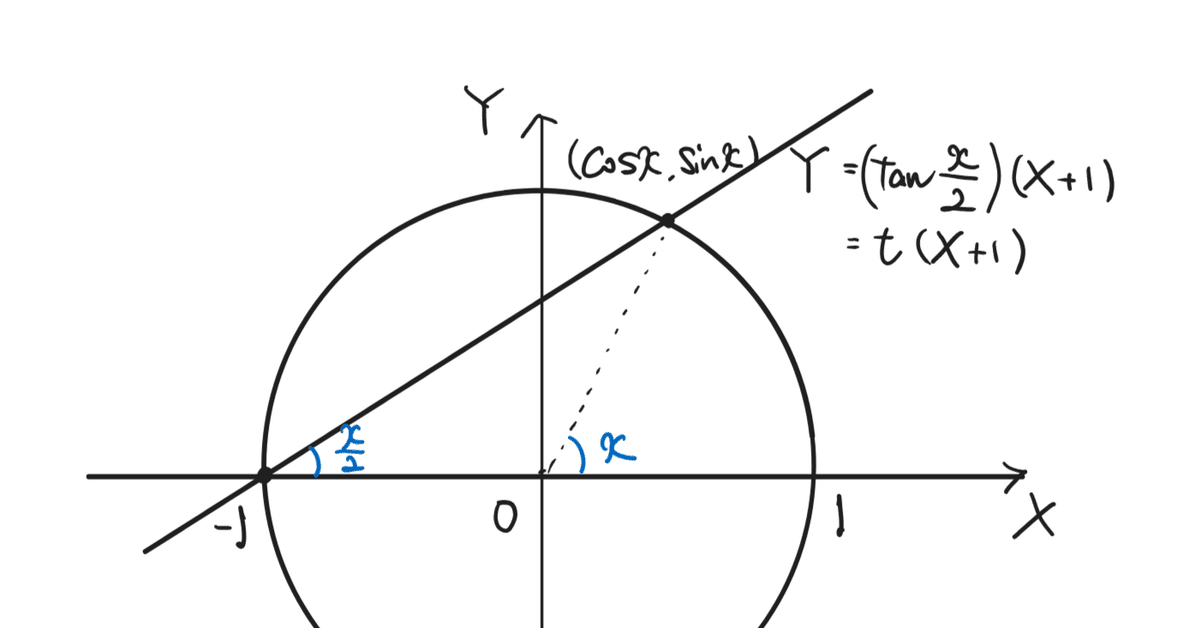
実はこれらは、図形的考えることができます。
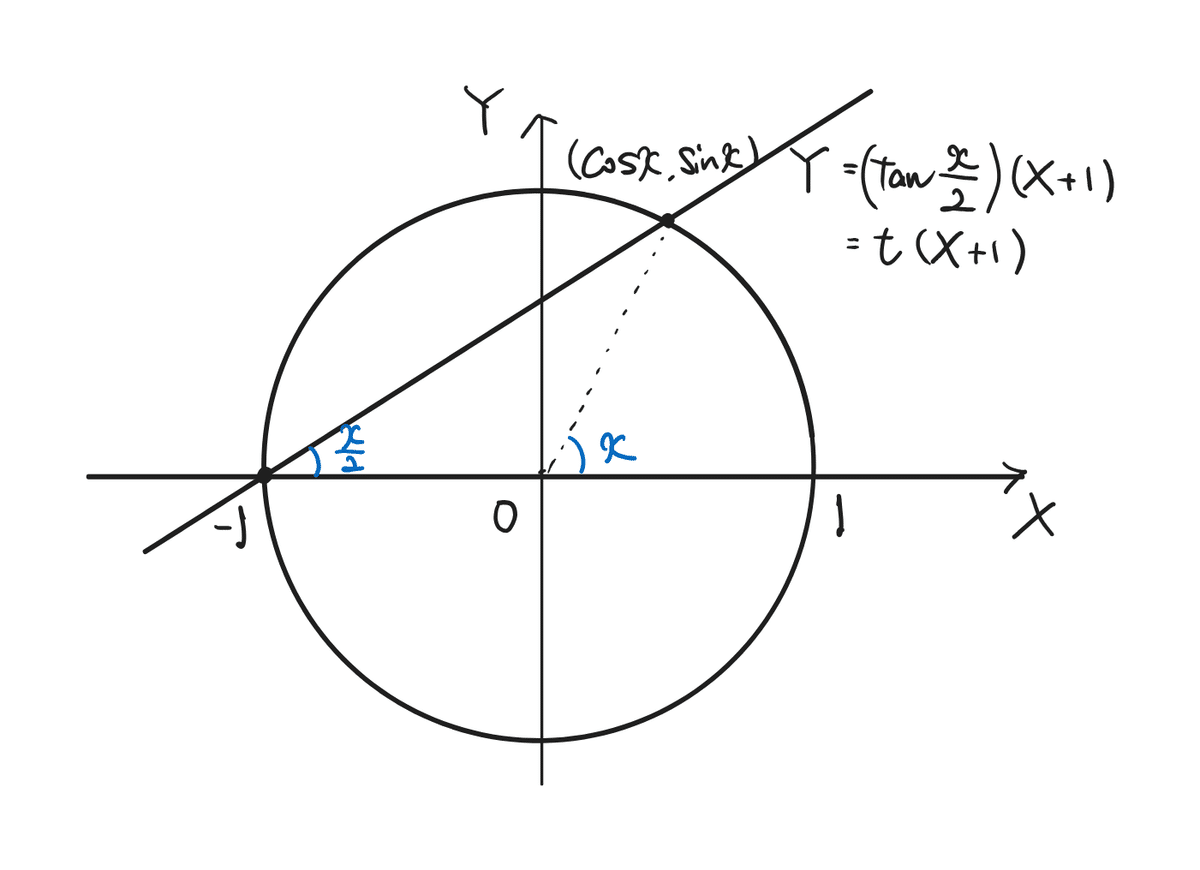
上のように単位円と傾き$${\tan \frac{x}{2}}$$で点$${(-1,0)}$$を通る直線との交点を考えます。円周角の定理から、真ん中の角度は$${x}$$であるから、交点は$${(\cos x ,\sin x)}$$で連立すれば、$${t}$$で交点を表すことができるので、さっきの計算と同じ結果を導くことができます。
