多項式除法の筆算の長除法と組立除法

多項式の除法を筆算する際、主に２つの方法が用いられる。１つ目は整数除算の筆算でお馴染みの長除法、２つ目はそれを簡略化した組立除法である。高校数学の教科書では長除法のみを例示し、組立除法は扱ってない。しかし、長除法よりも組立除法の方が記述量が少なく高速であるため、参考書や勉強サイトで扱われることが多い。

ところが、組立除法の計算の仕方を計算して手順の暗記になる場合が多い。組立除法が長除法の簡略化したものであり、その手順を追えば、自ずと対応関係が分かるようになる。そして、除数が二次以上の場合にも長除法に立ち戻れば容易に応用できる。

本記事では、筆算の長除法から出発し、幾つかの簡略化を経て組立除法に変形させる。

1. 除数が１次式の長除法

例題として (4x³ － x ＋ 7) ÷ (2x ＋ 3) を長除法で解く。

　　　　図1.1：　除数が１次式の長除法（標準版）

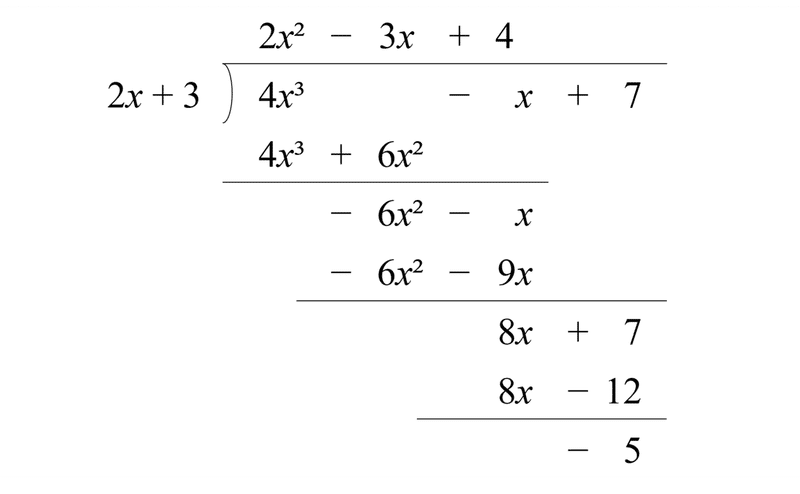
整数の長除法と同様に、最上位を消すように商を上位から立てて、立てた桁と除数の積を被除数から引いくのを繰り返す。具体に、4x³を消すように、4x³ ÷ 2x = 2x² を商の上位に立て、部分積 (2x＋3)×(2x²) = 4x³＋6x² を被除数 4x³ － x ＋ 7 から引いた余り出す。余りが１次未満の式になるまで余りを新しい被乗数と見なして繰り返す。こうして、商が 2x²－3x＋4 と余り－5 を得る。

確認も兼ねて、長除法でも省かれている情報を補ってみる。

　　　　図1.2：　除数が１次式の長除法（冗長版）

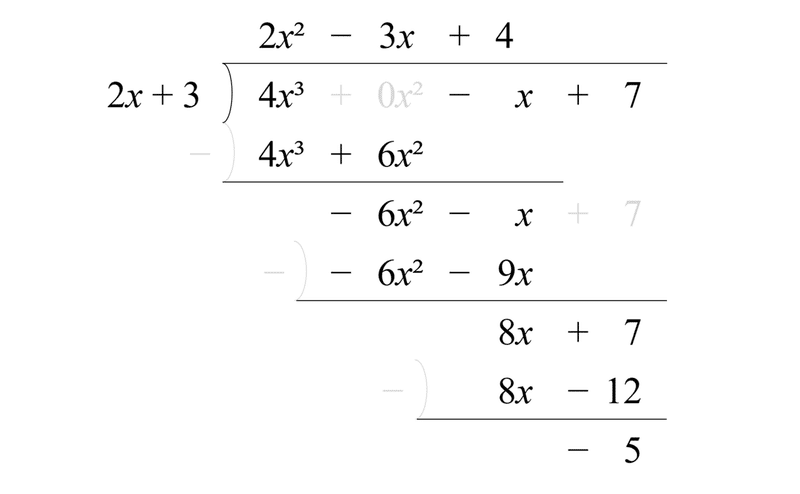
まず、係数が 0 の項は空白として書かれる。同類項が縦に揃っていれば正しく引けるため、省いても支障はない。次は、被乗数 4x³－x＋7 から部分積 4x³＋6x²を引いた余りは、厳密には －6x²－x＋7 である。しかし、＋7 が使われるのが次の繰り返しになるため、書く必要が無い。最後に、部分積を引いているため、各横線は減法の筆算である。これも除法の筆算に組み込まれるとして普通は書かない。ただ、組立除算では加法に化けるので、意識した方が良い。

以下ではこの長除法を徐々に簡略化していく。

　　　　図1.3：　除数が１次式の長除法（係数版）

まず目につくのは文字の部分である。縦に同類項で揃えているため、書かなくとも位置で分かる。そのため、文字を省いて係数のみで書く方法も良く用いられる。

ただ注意が必要なのは、文字が無くなるので係数が 1 の場合は 1 を明記する必要がある。また、空白も紛らわしいので、0 と明記すると良い。

　　　図1.4：　除数が１次式の長除法（簡略版）

次に目につくのは重複する係数である。既にあるなら、二度手間しなくても既に書いてあるのを読めば良い。

一つ目は部分積の最上位は被乗数の最上位を消すように商を立てるので、必ず一致する。図４では赤字で示した 4、－6、8 が該当する。薄く表示してる方は省ける。

また、余りから新しい被除数を作る際に、最初の被除数から１桁ずつ下ろしてくるが、それも省ける。引くときに上から直接引けば良い。図４では緑字で示した 1、7 が該当する。

ここまでスカスカに略すと、縦に押し込めば一気にコンパクトになる。

　　　図1.5：　除数が１次式の長除法（圧縮版）

図1.5は図1.4の横線が重なるように桁を上にずらしただけ。各余りの最上位と最終的な余りの境目が紛らわしくなるため、" ( " の句切りを入れてた。

この時点で、記述量が組立除法と同じになる。わざわざ組立除法の書き方を覚えなくてもこれでも良いと思う。ただ、２次以上への拡張や、引く際の符号処理の煩雑さを軽減するには、もう一工夫した方が楽ではある。

2. 除数が１次式の組立除法

　　図2.1：　除数が１次式の組立除法（折衷版）

計算時、各桁で商、部分積、余りの順に数字を書く。図1.5の例では 2, 6, －6,  －3, －9, 8, 4, 12, －5 の順に書くことになる。商を上に書く都合上、そこだけ筆が遠く移動し、不規則的な動きが入り、効率が下がる。そこで、組立除法では主に３つの工夫を施した。

① 商を余りの下の段に書く。これより、書き足す数字は、下の３段の間を順序良く移動できる。
② 除数の各係数を対応する各段の左端に書く。すると、商の見積もりでは、余りと除数の最上位の係数を見比び易く、部分積を計算する際も商と除数の下位の係数から計算し易くなる。
③ 除数の下位の係数の符号を反転しておく。代わりに、被乗数から部分積を引かずに足す。要は、部分積を出すタイミングで符号を反転させ、被乗数と部分積の減算を加算に変えている。符号を処理するタイミングを前倒しただけだが、減算する際の符号反転が無くなる分、加算の方が計算ミスし難い。

これより、計算手順は、
　　1-1)  便宜上、被乗数最上位の 4 を下す。
　　1-2) 左の 2 と見比べ、4÷2=2 を商に立てる。
　　2-0) 商 2 と－3を見比べ、部分積 2×(－3)＝－6 を次の列の上段に書く。
　　2-1) 被除数 0 と 部分積 －6 を足して余り －6 を計算して中段に書く。
　　2-2) 左の 2 と見比べ、(－6)÷2=－3 を商に立てる。
以下同様。

あとは書き方を変えるだけで一般的な組立除法になる。

　　図2.2：　除数が１次式の組立除法（標準版）

3. 除数が１次式で最高次係数が１の筆算

除数の最高次係数が１の場合、被乗数÷除数で商を立てるため、被乗数がそのまま商になる。その結果、商と余りの片方だけ書けば事が足りる。

まずは長除法の簡略版。被除数から部分積を引いた余りを直接上段の商に書き込むと図3.1の書き方になる。図3.1で同じ数字が商、部分積、余りの３ヶ所に現れるのを確認できる。

　　図3.1：　除数が１次式で最高次係数が１の長除法（簡略版）

次に長除法の圧縮版。部分積と余りを上に押し込んだだけ。

　　図3.2：　除数が１次式で最高次係数が１の長除法（圧縮版）

続けて組立除法の折衷版。除数の係数を各段の左側に分けて書き、部分積は符号反転で書き、減算を加算に置き換える。

　　図3.3：　除数が１次式で最高次係数が１の組立除法（折衷版）

そして、一般的な組立除法の書き方。

　　図3.4：　除数が１次式で最高次係数が１の組立除法（標準版）

余談として、１次式で最高次係数が１の場合、部分積を暗算してままの流れで更に被除数を加算すれば余りを出る。部分積は二度と使わないので省ける。それが多項式の短除法という筆算である。

　　図3.5：　除数が１次式で最高次係数が１の短除法

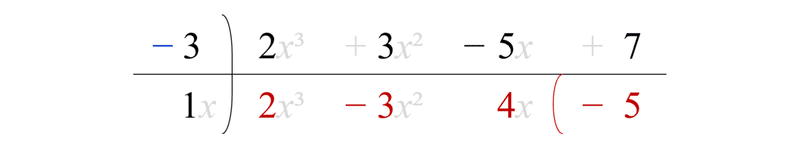
　　1) 左端の列から被除数 2 をそのまま商とする。
　　2) －3×2＝－6 に 3 を加えて －3 を商とする。
　　3) －3×(－3)＝9 に －5 を加えて 4 を商とする。
　　4) －3×4＝－12 に 7 を加えて －5 の余りを出す。

4. 除数が２次式の長除法

例題として (4x⁴ － 3x² ＋ 4x) ÷ (2x² ＋ 3x ＋ 1) を長除法で解く。長除法の場合、除数の次数が変わっても手順は全く同じである。

　　　　図4.1：　除数が２次式の長除法（標準版）

　　　　図4.2：　除数が２次式の長除法（係数版）

　　　　図4.3：　除数が２次式の長除法（簡略版）

ここで隙間を詰めるわけだが、除数が１次式の場合に比べ、残ってる数が多いため単純に上に押し込むだけでは綺麗にならない。１次式に比べて増えたのが緑字で示した部分積の３項目である 2、－3、2 であり、１次式の圧縮でも斜めに並んだ部分積を横１段に変えてるため、部分積の項ごとに段を作ると綺麗に並ぶ。

　　　図4.4：　除数が２次式の長除法（圧縮版）

具体に、赤字で示した各部分積の第1項の 4, －6, 4, 1 で下段を作り、青字で示した各部分積の第2項の 6, －9, 6 を中段とし、緑字で示した各部分積の第3項の 2、－3、2 を上段とする。

また、被除数からは２段分の部分積を引いて余りを出す。例えば、－3－2－(－9)＝4 、4－(－3)－6＝1 である。この多段の減算や符号の反転が計算ミスに繋がるため、加算に変えのが組立除法となる。

5. 除数が２次式の組立除法

除数が１次式の場合と同様、筆の移動距離を小さくする、規則的にするため、商を下に移動する。余りから商を割り出すときや商から部分積を出すときのため、除数の各係数を対応する段の左側に書く。

　　　　図5.1：　除数が２次式の組立除法（折衷版）

書き方を変えれば、標準的な組立除法になる。

　　　　図5.2：　除数が２次式の組立除法（標準版）

　除数の最高次係数が１の場合、１次式の場合と同様に商と余りが同じになり、最下段の商を省ける。

　　　　図5.3：　除数が２次式で最高次係数が１の組立除法（折衷版）

書き方を変えれば、標準的な組立除法になる。

　　　　図5.4：　除数が２次式で最高次係数が１の組立除法（標準版）

6. 補足：　商の計算順

第2節「除数が１次式の組立除法」の最後で示した計算手順は、標準的ではない。しかし、標準的な解法の方が非効率なため、本記事では採用しない。

標準的な手法では最高次係数を１の組立除法をベースとし、除数の最高次係数を１に変えてから計算した後に帳尻合わせで真の商を別に出す。例えば、第1節と第2節で使った例題 (4x³ － x ＋ 7) ÷ (2x ＋ 3) では、2x ＋ 3 の代わりに除数を 1/2 倍した x ＋ 3/2 で割ってから、商を 1/2 で割って帳尻を合わせる。

　　　　図6.1：　標準的な組立除法の第１ステップ

　　　　図6.2：　標準的な組立除法の第２ステップ

最初のステップとして、まず (4x³ － x ＋ 7) ÷ (x ＋ 3/2) を計算する。これは簡略化できる最高次係数が１の組立除法である。しかし、除数を1/2 にしてるため、この時点で得られた仮の商は、(4x³ － x ＋ 7) ÷ (2x ＋ 3) の真の商より 2 倍大きい。そのため、帳尻合わせとして、÷2 で真の商を出す。

ところが、第１ステップを計算する際、仮の商でもある余りから部分積を計算する際、大抵の場合は自ずと真の商を算出している。例えば、4 から －6 を計算する際、×(－2/3) を一気にする人は居なくて、4÷2×3＝2×3＝6 を計算してる場合、4÷2 が真の商になっている。除数の係数自体が元から分数の場合はともかく、整数係数の場合は商が必ず現れる。

以上の理由により、どうせ計算しているのなら、最初から計算して置けば良い。そうすると、以下の利点が得られる。
　　① 分数係数を扱わずに済む
　　② 最後に帳尻合わせをせずに済む（忘れ易い）
　　③ 筆を上から下へ、左から右へと統一的な動きにできる

標準的手順が２ステップに分けられる理由は、恐らく手順を覚えさせる流儀を取るため、簡略化できる除数の最高次係数が１の場合を先に覚えさせてから、一般的な除数を扱う流れになる。その場合、最高次係数が１の場合を流用した方が追加で覚える手順が少ない。ただ、これが逆に煩雑になり、組立除法を使う利点である計算速度を損なうことになる。

7. まとめ

多項式除算の筆算に長除法と組立除法が主に使われている。この２つは一見全く別の書き方に見えるが、やっていることが同じで、書く場所は違えど、各要素が対応している。対応関係さえ分かれば、長除法から組立除法を作り出すのは簡単である。