
ホタルビームとパリティの話
本記事はペンシルパズルI Advent Calendar 2020の13日目です。
こんにちは。lilvaです。この記事では自作のホタルビームについての話をします。個人的にパリティが好きというのもあり、パリティとの関係を意識して話したいと思います。適宜読み飛ばしつつ眺めていただければ幸いです。
0. 初めに
改めてこんにちは。lilvaです。今まで決めずにいたのですが、読み方は「りるば」ということにしました。本日は12月13日ですが「13」といえば何が思い浮かぶでしょうか?……そう、成宮由愛ちゃんの年齢ですね!!私はペンシルパズルを作り始めて1年ほどになりますが、きっかけはSUPER7638WEEKの時、それ以降楽しくパズルを作ったり解いたりしています。パズルへのきっかけを作ってくれたふーなんとかさんには感謝しています。感謝も込めて今年の7638PGPでは積極的に参加させて頂いたのですが、少しやりすぎたような気がしなくもないですね……。76×38のパズルなんてもうなかなか作る機会もないでしょう。その解説も鋭意製作中なのでお楽しみに……?
なお13は私の好きな白菊ほたるちゃんの年齢でもあります。ほたるちゃんかわいい。ほたほた。ちょうど1年くらい前のこと、「お、ホタルビームなんていうパズルがあるぞ。……なかなか楽しいな。よし、自分でも作ってみよう。」と闇に飲まれてしまったのをきっかけにホタルビームをひたすら作ってはや1年。ホタルビーム楽しいです。今まで種明かしを避けてきたホタルビームがあるので本記事はその解説をしたいと思います。
1. パリティとは
ホタルビームの話に入る前にパリティとは何かを軽く共有しておきます。私よりもよくわかっている方、たくさんいらっしゃると思いますので適宜読み飛ばしてください。
パリティとは……偶奇という意味です。偶数か奇数か、2で割った余りが0か1かということに注目する考え方を総称してパリティと言います。(間違っていたらごめんなさい。) 必ず偶数、必ず奇数という場合もありますし、偶数と奇数で状況が異なるという場合もあります。
実際に出てくる場面はとても多く、様々な形でパリティは現れます。最もよく見るのは本数定理でしょうか。これは「線の端は常に2つ1組」という性質から、最終的に端のないループ系の線引きパズルにおいて「任意の領域について領域を出入りする箇所は偶数個」という性質が成り立ちます。使えるパズルはスリリン、ヤジリン、ましゅ、などなど。ホタルビームは端のあるパズルなので使えません。
パリティを使った話は色々ありますがここでは特に紹介したい有名問題を2つ。
ナイト・ツアー
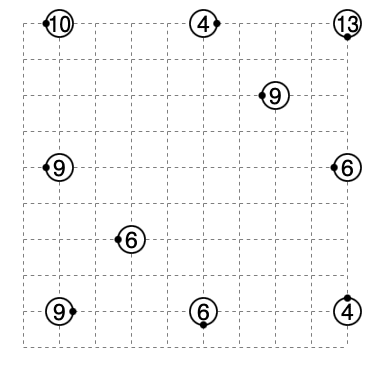
チェスのナイトを動かす問題です。ここでは特に次のような問題を考えます。
「右図に示されるようなナイトの動きで、左図のSのマスから全てのマスをちょうど1度ずつ通ってGのマスへ行くことは可能か?」

……はいそうです。市松です。右の図で分かる通りナイトは白のマスと黒のマスを交互に移動するため黒マスのSから出発して64マス踏破したときには必ず白マスにいるはずです。よって条件を満たす移動はありません。
市松は背景にパリティがあります。次のように言い換えてみます。
マスを自然な2次元の座標と見たとき、ナイトの移動は(±1,±2),(±2,±1)(複号任意)と表すことができます。このいずれの場合においても横方向の移動量と縦方向の移動量を足し合わせたとき奇数となることに注目します。始めのマスを(0,0)、n回の移動後(x,y)にいるとき、nが奇数であればx+yも奇数、nが偶数であればx+yも偶数ということになります。従ってちょうど63回の移動で(7,7)であるGのマスに到達することはできません。
市松塗り分けは横方向と縦方向の和に注目したとき偶数か奇数かによる色分けと見ることができます。今回はナイトの移動で考えましたが、通常の線を引く問題においても(0,±1)か(±1,0)と見ることで同様の市松による議論ができます。難しいシンプルループをやりましょう。また説明はしませんが分割系のパズルなどでも市松塗り分けが有効であることがあります。
サム・ロイドの14-15パズル
超有名なやつです。パズル作家サム・ロイドが懸賞金をかけたことで知られる、下図の配置のスライディングパズルに解がないことの証明でパリティが出てきます。

今回は数学の置換の話がしたいわけではないので深入りはしません。要点のみ説明すると左の図と右の図は14と15の「1回」の入れ替えであること、空白マスを右下の位置に戻すには必ずのべ「偶数個」のタイルを動かす必要があること、そしてそれらが両立しえないことが数学的に言えるという話です。
空白マスの動きは交差可能なループを作ります。移動を(±1,0)か(0,±1)と見て市松を考えると、初めと同じ右下に戻ってくるときには初めと同じ色に到達する事になるため、動かす回数は偶数回となります。
パリティといえばまずはこれ!という話題ですので紹介しました。このように様々な場所にパリティを見出すことができます。
2. 「角」の手筋
さて本題です。まずホタルビーム含め一般に線の曲がり角について何らかの制約が与えられているパズル(主にDetourですが)について考察します。
2-0. 注意事項
この記事においては線の曲がり角のことを全て「角(かど)」と呼びます。また特に2次元のマスの縦横に対し平行な線を引くパズルのみについて考えます。つまり鋭直鈍ループのような自由線を引くパズルや3次元以上に拡張されたパズルは考えません。線の引き方としてはマスの中央に引くパズルと辺に沿って引くパズルがありますが、基本的に前者に沿った書き方をします。
2-1. 基本性質
まず角の定義を一つ決めると次のようになります。
定義. 角とは縦方向と横方向にちょうど1本ずつ線が伸びるマスである。
色々定義の仕方はありそうですが、今考えているようなパズル種の中ではこれで問題はありません。ここから次の基本性質が得られます。
1. 角であるマスにおいて線の通らない辺の対辺には線が通る。
1'. 角であるマスにおいて線の通る辺の対辺には線が通らない。
2. 向かい合う辺の片方に線が通り、片方に線が通らないならばそのマスは角。
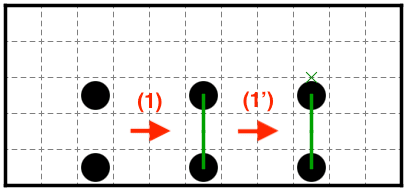
例1:(ましゅ) 1より辺の黒ましゅから縦に線が伸び、1'より通らない辺がわかる。
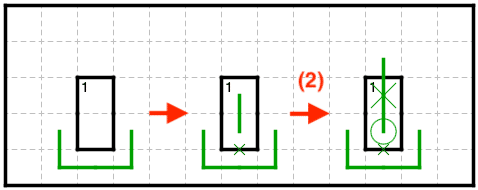
例2:(Detour) 小ループ回避より縦に線が伸び、2より角の場所がわかる。
(角のマスを◯、角でないマスを×で表しています。)
逆に直進するようなマスについては、通らない1辺があればその辺に平行に線が通るという性質が分かります。
2-2. 1×nの挙動
次に1×nの領域に曲がる回数の指定が与えられている場合を考えます。このとき前節の一般化となる性質が得られます。基本的にはDetourくらいでしか使いようがないのですが、一部充填系のホタルビームでも適用することができます(後述)。また以下で述べる性質は角内外理論から導かれる性質の特殊な場合です。
説明のしやすさの面から縦1、横nの長方形を説明に使います。縦長の長方形でも成り立つことは同じです。まず1つ目の主張から。
命題2-1. 両端を線が通過しない1×nの領域において領域内の角の個数は偶数個。
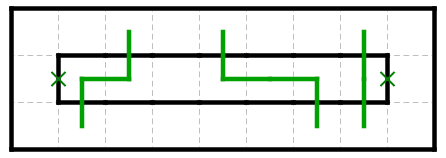
証明: (領域内の角の個数)=2×(領域内の横線の本数)である。[証明終]
角の基本性質は縦線と横線が1つずつということです。領域内の角は必ず領域内の横線の端になっていなければなりませんので自然にこの性質が成り立ちます。またこの性質は昨年のSP1さんの大域手筋まとめでも紹介されていました。
今想定しているパズルは主にDetourですが、この性質に全マス通過は無関係であることを注意しておきます。線の通らないマスがあっても同様の性質が成り立ちます。
偶数個ということでパリティが顔を覗かせてきました。両端を線が通過しないことを前提としましたが、両端を計算式に組み込めば更に次のように拡張できます。
命題2-2. 1×nの領域において「両端の2辺で線が通過している個数」と「領域内の角の個数」の偶奇は一致する。
証明: dL=(両端の2辺で線が通過している個数) (dL=0,1,2)、C=(領域内の角の個数)、L=(領域内の横線の本数)とおく。このとき、dL+C=2Lである。従ってdL≡C(mod 2) [証明終]
(a≡b(mod 2)は2で割った余りが同じという意味です。)
特に具体的な適用の形では次のように言えます。
1×nの領域について、
1. 領域内の角の個数と片方の端の様子がわかれば対辺の様子もわかる。
2. 領域の両端の様子がわかれば、領域内の角の個数の偶奇がわかる。
ここまでが1×nの挙動になります。数行にまたがるような場合についても1×nに分割することで適用することができます。
↓挙動一覧。奇数をo(odd)、偶数をe(even)で表します。

……さて、この辺の話を思いついたのが半月くらい前7638点ホタルビームの76と格闘していたときです。便利だと思いこの性質を使った問題を意気揚々とパズスクに投稿してみたところ、より一般化された理論を知ることになるのでした……。
2-3. 長方形部屋の内外定理
提唱は焼きもうふさんより。通称角内外理論。上記性質の一般化です。ただし本記事の以降では使わないためここでは紹介に留めます。
定理(長方形部屋の内外定理)
長方形の領域において、「領域内の角の個数」と「長方形の4頂点のうちループの内部(外部)にあるものの個数」の偶奇は一致する。
2-4. 線に与えられた制約
もう一つ、角の性質としてあげられるものがあります。上で考えていたのはDetourのようにマスに対して角であるかの制約が与えられる場合ですが、ホタルビームではホタル同士を結ぶ線に対して角の個数の制約が与えられます。このとき、縦線と横線は交互に来るためパリティから次の性質が言えます。
定理(湾岸道路定跡)
縦線は奇数回曲がると横線に、偶数回曲がると縦線になる。
横線は奇数回曲がると縦線に、偶数回曲がると横線になる。
命名者は半袖さん。こちらのブログで解説されています。この性質が使えるのはホタルビーム特有という感じがあり、信濃川理論と並んで好きな性質です。自分はこの性質を悪用した結果、ホタルビームが闇に染まりました。
余談ですがこの性質はキンコンカンでも確認できます。ただし両端がわかっているキンコンカンでは使う機会がありません。
3. 充填と損失
2章では角について一般の性質を考えましたが、3章では内容を充填系のホタルビームに絞って考えます。
3-0. 問題
以降の解説は次に示すTwitterにあげた問題の種明かしになります。先に解いておきたいという方はご確認ください。
問題3.1 (8×8)
Twitter: https://twitter.com/lilva_0419/status/1277164839136382979
ぱずぷれ: http://pzv.jp/p.html?firefly/8/8/a45d32e2bn33d48j33c19i35b34a34a
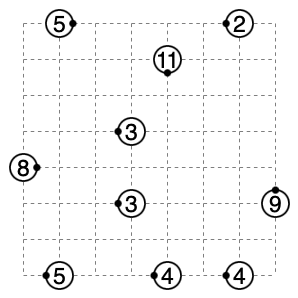
問題3.2 (5×5)
Twitter: https://twitter.com/lilva_0419/status/1229000064128802821
ぱずぷれ: http://pzv.jp/p.html?firefly/5/5/b813v

問題3.3 (17×17)
Twitter: https://twitter.com/lilva_0419/status/1329120689861783554
ぱずぷれ: http://pzv.jp/p.html?firefly/17/17/y873zg853zg833zg813zzzzzze

問題3.4 (12×12)
Twitter: https://twitter.com/lilva_0419/status/1227450355396628480
ぱずぷれ: http://pzv.jp/p.html?firefly/12/12/a36c27e2as34c26m1dc38n15f34n46c46m16c43s1ce36c3fa
パズスク: https://puzsq.jp/main/puzzle_play.php?pid=6684
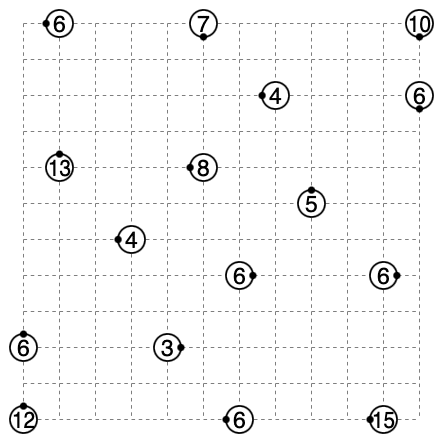
問題3.5 (10×10)
Twitter: https://twitter.com/lilva_0419/status/1277527224804048896
ぱずぷれ: http://pzv.jp/p.html?firefly/10/10/a3ac44c2dq39m39g36m36q49c26c14j
3-1. 素朴な不等式
上であげた問題はホタルの数字が大きく、全体の多くを角で埋め尽くすような完成形になると予想されます。解き方はうまく詰め込むように引いていくのが良いと思いますが、唯一解保証をしなければならない作者はそうはいきません。作る上で闇雲に探索しなくても良くなるように大域的な仕掛けが用意してあります。
ホタルビームについて次の不等式が成り立ちます。
命題3-1(ホタルビームの不等式1)
領域内のホタルの個数をF、角の個数をC、領域のマスの個数をSとする。このとき、F+C≦Sが成り立つ。
特に等号が成立するとき全てのマスに通る線が存在し、ホタルのいない全てのマスは角である。
特に左辺と右辺の差が小さく、マスのほとんどが角であるようなホタルビームを充填系のホタルビームと呼ぶことにします。ホタルビームは辺に引くパズルなので曲がる点はマスではありませんが、本記事では形式的にマスと呼びます。
例として問題3.1を考えます。この場合盤面上のホタルの個数は10個、線の曲がる回数の合計は54、盤面サイズは64です。よって等号が成立し、全てのマスを線が通過し全てのマスで線は曲がります。マスが角であることがわかれば角の基本性質から容易に解けます。
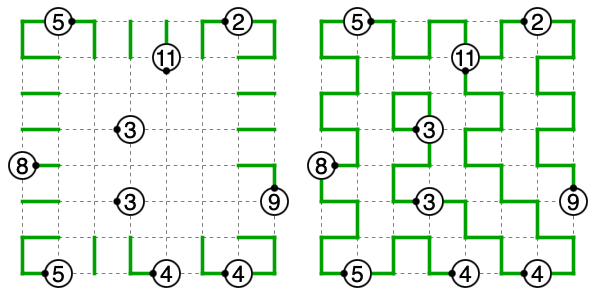
この等号が成り立てば話は簡単なのですが、実際には盤面や配置に由来する制約が存在するため、作者が仕込まない限り簡単には成り立ちません。そこでそれらの制約を不等式にさらに加味して考えます。
命題3-2(ホタルビームの不等式2)
領域内のホタルの個数をF、角の個数をC、領域のマスの個数をS、領域内の制約により曲がることのできないマスの個数をLとする。このとき、F+C≦S-Lが成り立つ。特に等号が成立するときLとして想定した制約の限界まで角が入る。
さてこのLをここでは「制約由来の損失値」と呼び、次節以降で具体的な制約をいくつか考察します。制約全体を把握できているわけではなく、あくまでいくつかの具体的な場合についての考察です。「最低限こんな制約がある」という形でLに対して下からの評価を与えることができます。
3-2. 1×n損失 / 隅損失
まず一つ目の損失が上述の角の性質から即座に導かれます。
命題3-3. 1×n領域について、両端の様子から領域内の角の個数Cの偶奇がわかっているとする。Cとnの偶奇が異なるならば領域内に角でないマスが1つ以上存在する。
例えば1×7の領域で偶数回曲がることがわかっているのならば、少なくとも1マスは線が通らないか線が直進するマスということになります。
領域内にホタルがいる場合には成り立ちません。
もう一つ簡単なものとして小ループ禁由来の次の損失があります。
命題3-4. 下図に示されるような「隅」の領域について角でないマスが1つ以上存在する。
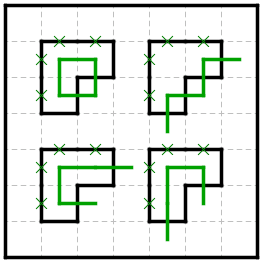
図のような形で通らない辺が与えられているとき、領域内3箇所全てで曲がると即座に小ループを作ります(図左上)。よっていずれか1箇所は角ではありません。角でない場所が1箇所のみであるようなパターンは図の3通りのいずれかです。
これも領域内にホタルがいる場合とくぼみの位置に③のホタルがいる場合(ループを作ることができる)には成り立ちません。
1×n損失と隅損失を数えることで等号が成り立つ場合があります。
例えば問題3.2について考えます。下図の囲まれた領域内それぞれで損失が最低1ずつあるためL≧5であることが分かります。F=1, C=19, S=25, F+C≦S-LよりL=5で等号成立します。このとき、囲まれていない領域は全て角であることが分かります。また2色の青領域についてはその青領域全体で損失が1でなければならないので共通部分が角でないマスになります。各赤領域にはちょうど1つずつ角でないマスがあります。
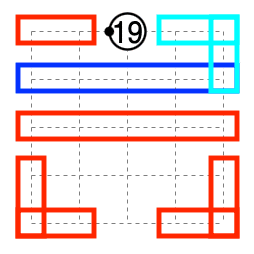
確定箇所を引くと新たに赤丸のマスが角にならないことが分かります。言い換えると3段目の残りのマスは全て角です。
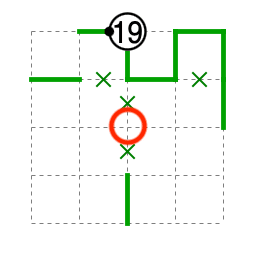
よってさらに確定箇所を進めて完成です。
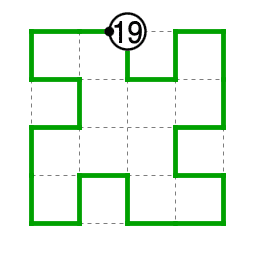
問題3.3についても一例として次のように見るとL≧17であり、L=17で等号が成立することを確認できます。

解答図(ネタ問です)

Detourについても1×n損失、隅損失を加味した不等式評価は有効です。
問題3.6 (Detour、8×8)
puzz.link: https://puzz.link/p?detour/8/8/000h6pm8g00003vjpg1svs00g036g4041g
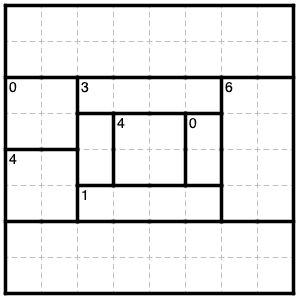
ヒント: 8マスの6は高々2つまでしか角でないマスを持てません。
3-3. 市松損失
前節はマスに対する制約を考えました。線に対する制約もあります。パリティの力を使いましょう。
白黒2色に塗り分けた市松を考えます。このとき同じ色に到達するときには線の長さは偶数、異なる色に到達する時には線の長さは奇数になります。
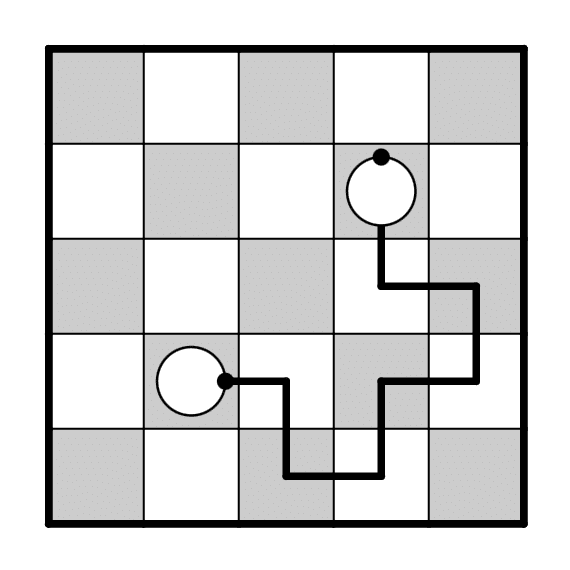
ホタルビームでは自分自身に到達する可能性があるので常に同色の繋ぐ当てはあると考えて良さそうです。一方で異なる色の繋ぐ当ては必ずしもあるとは限りません。もし作者が(悪意を持って)市松の一方のみにホタルを配置したとするならば、全ての線の長さは偶数になります。
線の長さは(途中に通過するマス数)+1で計算できるので、上の制約は必ず途中に奇数個のマスを経由するとも言えます。線の曲がる回数が偶数であったならば経由するマスのうち少なくとも1マスは角でないマス、この場合直進するマスになります。
命題3-5. 市松を考えたとき、偶数回曲がって同色のマスに到達するならば、その経路に角でないマスが1つ以上存在する。
行き先が湾岸道路定跡などで決定づけられる場合には、「奇数-異なる色」のパターンを使うことも可能だと思います。(作ったことはありませんが。)
命題3-5の適用例として問題3.4を見ます。この場合、市松制約に注目すると全てのホタルが同色なので自動的に偶数のホタルの分だけ損失が発生します。F=16, C=117, S=144, L≧11です。まさにL=11で等号が成り立つので、偶数のホタルの経路上にはちょうど1箇所角でないマスがあります。奇数のホタルの経路上は全て角のマスです。また命題3-5で生じる損失は全て直進の形で現れるため、全てのマスに通る線が存在することが分かります。
前節とは異なりいきなり多くのマスが角と決まるわけではないため、制約を意識しながら先読みなどを使う必要があります。
唯一解確認までの流れ
初期盤面
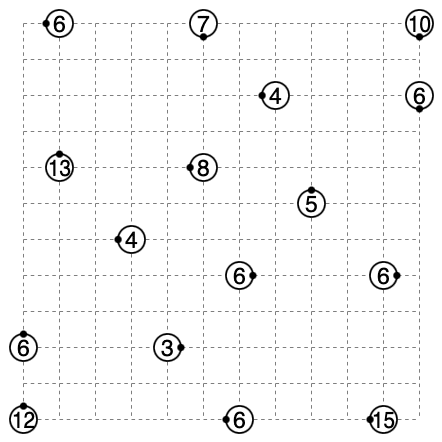
全マスで曲がることのわかっている奇数を優先的に埋めていきます。
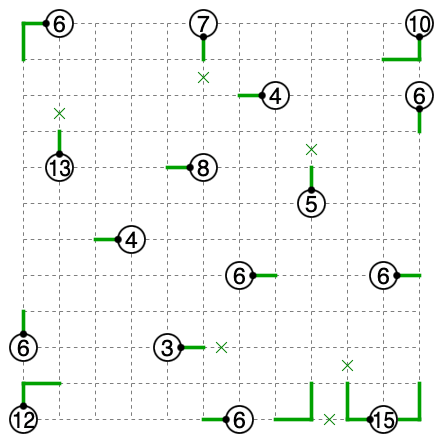
15を右に進めると破綻します。
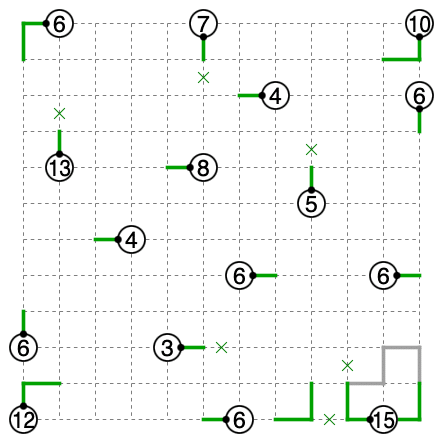
15が確定し、ループができます。信濃川理論よりこれ以上ループはできません。

3→6→12と埋まっていきます。図の12は以降全て曲がります。
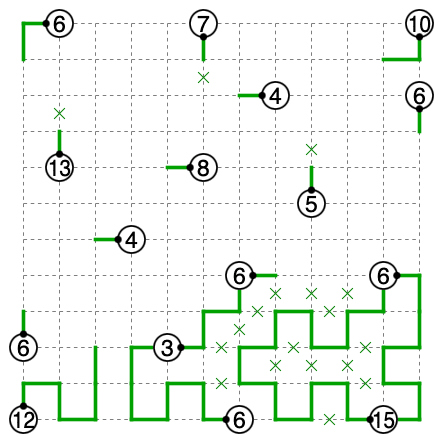
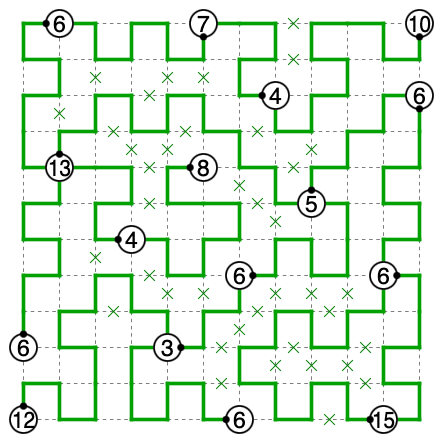
残りは「全部のマスを通過すること」「奇数は通過する全マスで曲がること」「偶数は1回を除いて全マスで曲がること」に気をつければ埋まります。
解答図
さて以上が具体的な制約でした。最後に不等式を再掲します。
命題3-2(ホタルビームの不等式2)(再)
領域内のホタルの個数をF、角の個数をC、領域のマスの個数をS、領域内の制約により曲がることのできないマスの個数をLとする。このとき、F+C≦S-Lが成り立つ。特に等号が成立するときLとして想定した制約の限界まで角が入る。
Lに含まれるものとしては1×n損失、隅損失、市松損失などがあげられ、Lはそれら全てを考慮した値である。
え…?まだあるって?
問題3.5を考えます。このとき、F=10, C=76, S=100, L≧6ですがこれでは等号成立しません。もう一度考えてみます。
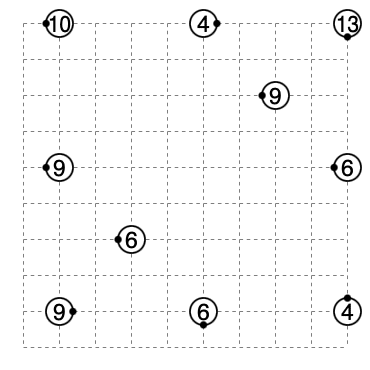
3-4. ギンガムチェック損失
線を引くパズルにおいて市松が有効な場合は多いです。しかし縦と横の和を取る市松ではなく縦と横を分離して精密に考えると新たな制約が見えてきます。次の問題を考えます。
問題: n回連続で曲がるとき、その始点と終点にはどのような関係があるか?
解答: 連続で曲がるときには必ず(a):(±1,0)と(b):(0,±1)を交互に繰り返すことになる。始点を(0,0)として、
(i) n≡0(mod 4)のとき、始めが(a)からならば(a)が奇数回、(b)が偶数回となり、終点は(o,e)。逆に(b)からならば終点は(e,o)。(o:奇数、e:偶数)
(ii) n≡1(mod 4)のとき、(a)と(b)はともに奇数回。終点は(o,o)。
(iii) n≡2(mod 4)のとき、(a)からならば(a)が偶数回、(b)が奇数回で終点は(e,o)。逆に(b)からならば終点は(o,e)。
(iv) n≡3(mod 4)のとき、(a)と(b)はともに偶数回。終点は(e,e)。 [解答終]
縦横に分けて考えることで少なくともこのような事実が分かります。充填系のホタルビームの挙動は市松ではなく縦方向と横方向それぞれの偶奇を考えることでより精密な評価が可能です。
問題4.5について考えます。ホタルの配置は縦方向にも横方向にも間隔が偶数になるように調整してあります。このとき、
◯数字が4で割って3余る数であれば、経路上全マスで曲がっても縦横偶数ずれたマスにたどり着くので損失はありません。
◯数字が偶数であるならば、経路上全マスで曲がったとき最終到達点は(o,e)ないし(e,o)ずれたマスになります。よって奇数になる側を調整する必要があります。これは奇数である方向に経路途中で奇数回の直進を追加することで可能です。損失は最低1で、その際に直進する向きは数字と始めの向きから決まります。
◯数字が4で割って1余る数であれば、経路上全マスで曲がったとき最終到達点は縦横奇数ずれたマスになります。よって損失は最低2で縦横両方向に奇数回直進します。
損失に合わせて色分けをすると図のようになります。ギンガムチェックです。白マスから白マスへ行きたいとき、全マスで曲がろうとすると薄い青に到達する場合(=偶数)であれば損失1、濃い青に到達する場合(=4で割った余りが1)であれば損失2です。

それに従って損失値Lを再計算すると、以下の問題3.5において偶数が6つ、4で割って1余る数が4つあるので、L≧1×6+2×4=14。F=10, C=76, S=100なので等号が成立します。従ってこの問題は次のような性質が成り立ちます。
◯全てのマスに通る線が存在する。
◯偶数は縦方向か横方向(ホタルにより決まる向き)にちょうど1回直進する。
◯9, 13は縦方向と横方向にちょうど1回ずつ直進する。
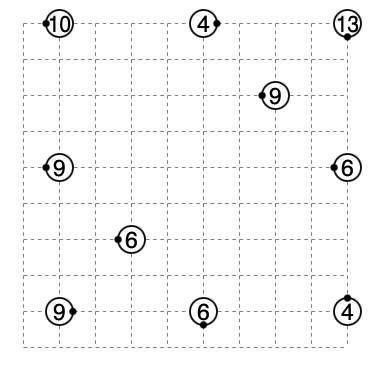
あとはこの性質を気にしつつ適度に先読みをしてあげれば唯一解であることが確認できます。
唯一解確認までの流れ
まず全マス通過に注意します。
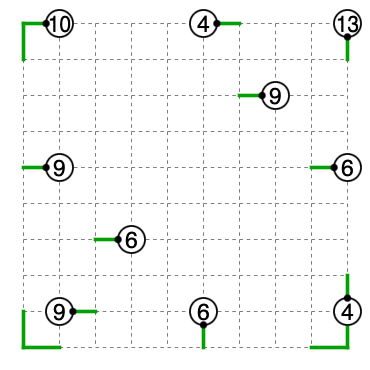
13は9と6の間を通過する必要があります。全マス通過であること、同じ向きの直進が高々1回であることに注意します。
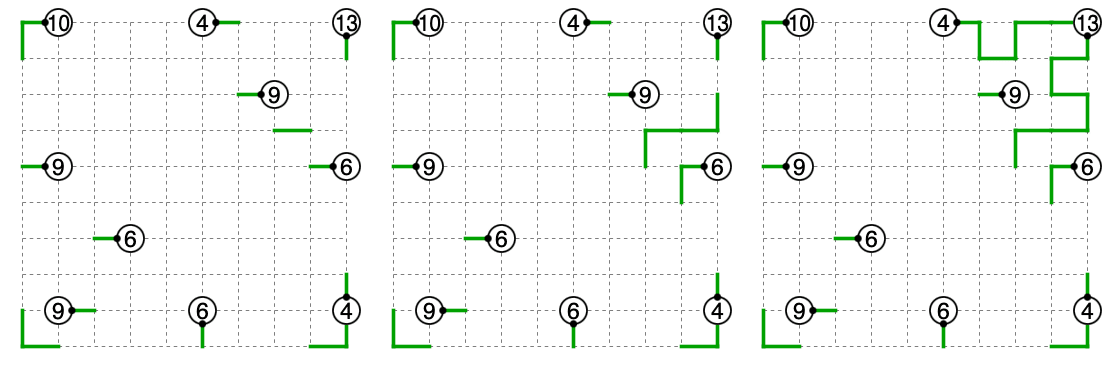
右端列の4と6における調整の直進は縦方向です。4は縦方向に4マス分横方向に2マス分動ける、6は縦方向に4マス分横方向に4マス分動けるとも考えられます。探してみるとこの条件で辿り着ける先は1箇所しかないことが分かります。
ループができました。信濃川理論よりこれ以上ループはできません。
左の6についても縦横の構成要素を調べて繋ぎ方を考えると以下の3通りがあることが分かります。うち1つ目は一番左の列が直進に関する条件に合いません。

2つ目のパターンを考えます。10の調整の直進は縦方向です。4に繋がることが分かるので全マス通過から線は上辺に沿います。
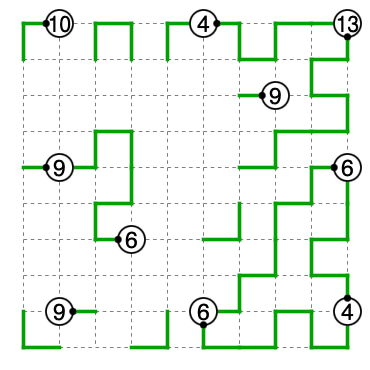
10の左右の縦線が共にすぐ曲がるとすると横方向の直進ができてしまいます。よってどちらかが直進になります。下図のようになり、これは直進が連続するため破綻しています。
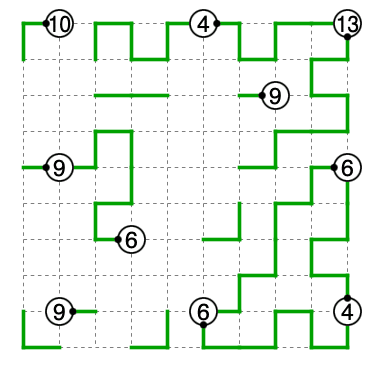
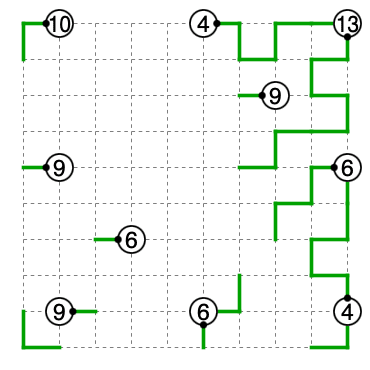
よって3つ目のパターンを考えます。まずここまで進みます。
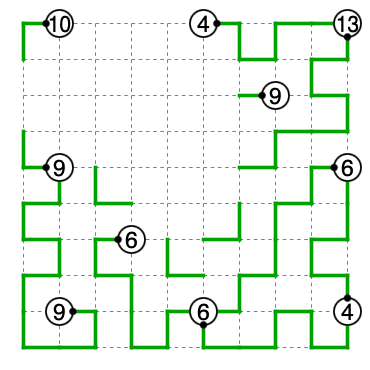
10を9に繋げると9の繋ぐ当てが無くなるので10はやはり4に繋がります。2択は先読みで確定します。
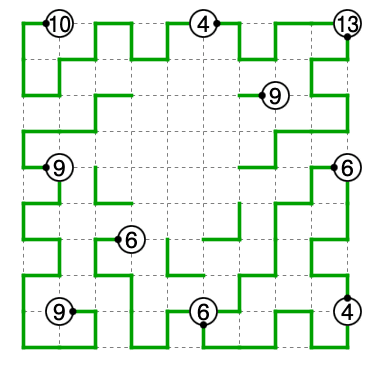
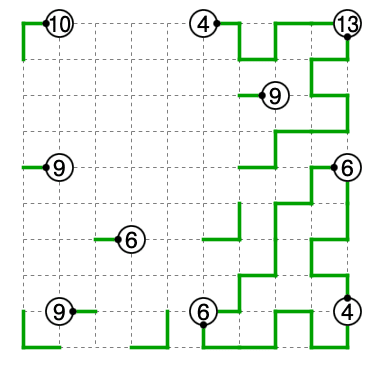
あとは性質に注意して埋めます。
途中経過

解答図
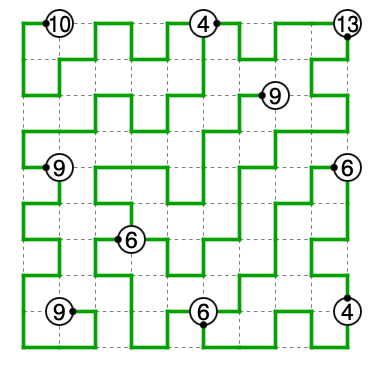
以上よりこの問題は唯一解であることが分かります。
4. 終わりに
結局のところ何が言いたかったかというと、上に書いてあることはどうでもよくてホタルビーム楽しいなという話です。色々なパズルにそのパズル特有の非自明さの深淵みたいなものがあってそれを理論で照らしてみることにどこか楽しさを覚える、そんな気持ちの結果得られたものをひたすらに書き連ねてみました。書き連ねたら大変に長くなってしまいました。
以上、lilvaによる充填理論報告でした。読んで頂いた方、ありがとうございます。おまけの章は私からの闇のおすそ分けです。
5.演習問題
おまけです。拙作ですが余力のある方はどうぞ。易しい問題はありません。
問題5.1 (Castle Wall、10×10)
パズスク: https://puzsq.jp/main/puzzle_play.php?pid=12591
puzz.link: https://puzz.link/p?castle/10/10/041l042d021b041p032b243p234b044p034b042d013l036
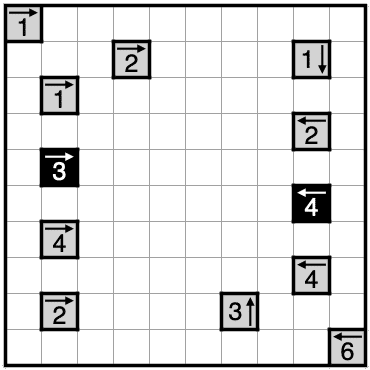
コメント: 市松だけがループ系で使えるパリティではないです。
問題5.2 (Detour、9×10)
パズスク: https://puzsq.jp/main/puzzle_play.php?pid=12806
puzz.link: https://puzz.link/p?detour/10/9/000000o1g000000000000100010000000-4f1
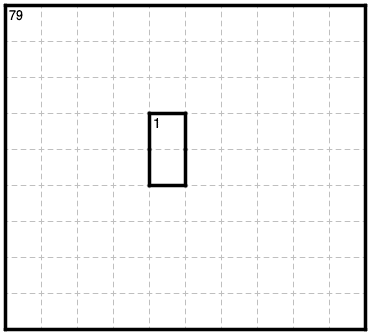
コメント: 引かないで解くことを強要しません。引いた方が早いかもしれません。
問題5.3 (キンコンカン、8×8)
パズスク: https://puzsq.jp/main/puzzle_play.php?pid=12807
ぱずぷれ: http://pzv.jp/p.html?kinkonkan/8/8/vvvnrvvvvvvgvvvvvvvvvvvgAbBBkAo-1d-40-40-1d
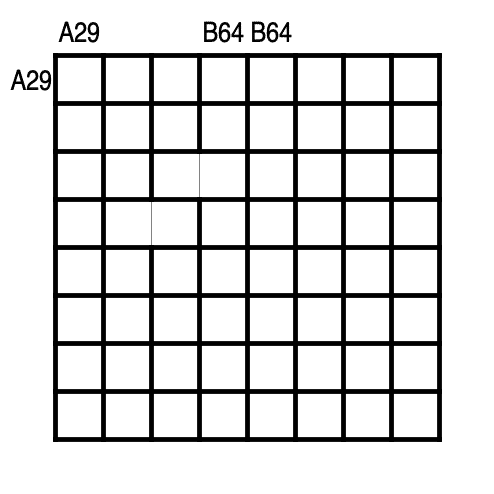
コメント: キンコンカンも角を持つパズルですね。でもこんな見た目ではなかったと思うのですが。
問題5.4 (ホタルビーム、12×12)
ぱずぷれ: http://pzv.jp/p.html?firefly/12/12/43e46c46m911g35q36g19f4bf27g14q19g35m26c49e3cm
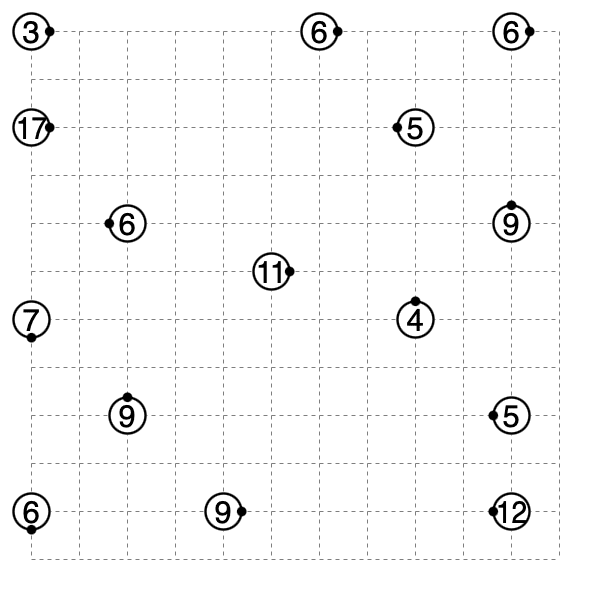
コメント: パズスクには充填系ホタルビームをあまり投稿したくないのです。(見た目が似通っているため。)
