MATLAB Functionブロックを使おう!~ Running σ
前書き
前に「MATLABとSimulinkと私 (思考を止めない開発ツール)」で、
開発過程として、
「SimulinkのブロックをMATLAB Functionで置き換える」
ということを書きました。
今回はその具体例を、「Running σ」を題材に書こうと思います。
(noteでは数式が書けないようなので、文章中の数式表現が数式画像部分と合わない点はご容赦ください)
統計的特徴量
音楽信号の特徴量解析などで、判断のための閾値を統計量から自動で決定したい場合があります。よくあるのは μ(平均値)± nσ(標準偏差)です。
今回はこれ自体の説明はしませんが、対象が正規分布であれば、μ±σには約68.3%、μ±2σには約95.4%、μ±3σ には全体の約99.7%が入るという統計量です。対象が正規分布に従わない場合でも、統計的な意味合いは変わってきますがある程度の基準値として用いることは可能です。
一般的には移動平均/分散が用いられることも多いのですが、場合によっては局所的な変化ではなく、曲全体での値が欲しいこともあります。
対象がローカルファイルであれば問題ないのですが、ストリーム等で、リアルタイムに値を更新したい場合は困ります。
その場合、Running μ/σという手法をとることがあります。
名前の通り、データが入ってくる度に、過去の全データを使って μ/σ を更新します(任意の時点でリセットしたりももちろんできます)。
実際の音楽信号(見やすくするために絶対値を取っています)と、移動(μ+3σ)(ブロック長=4096)、Running (μ+3σ)、Running (μ+1σ)、を以下に示します。
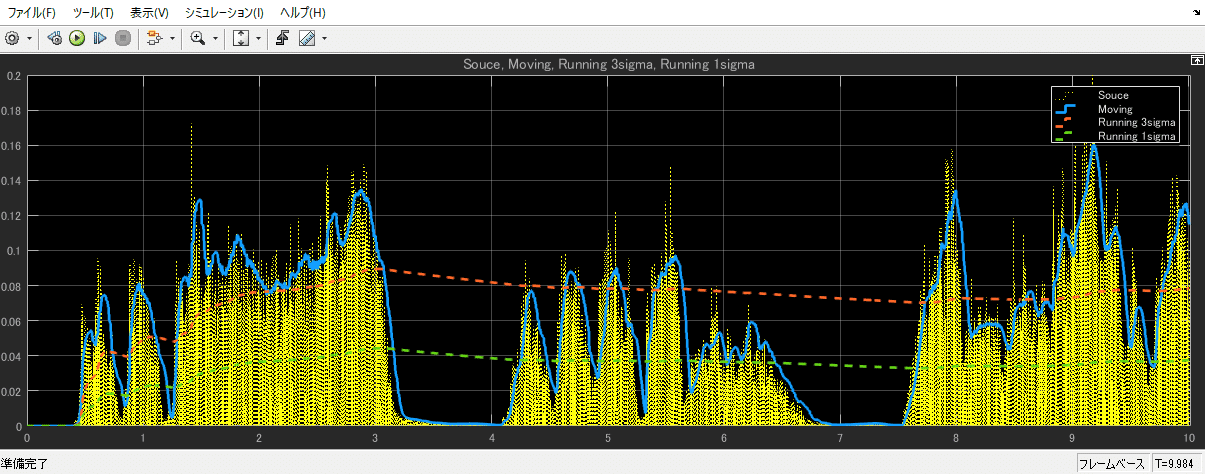
それぞれ、違った目的に色々使えそうですね。
Running μ/σ は、Simulinkでは "Mean/Standard Deviation" ブロックのパラメータ、"Running mean/Running standard deviation" をチェックするだけで計算できます。

しかし、組込系で使いたいけど Simulink Coder を買うお金はない、あるいはコードを最小・最適化したい場合等は自分で作るしかありません。
ここで問題になるのが、普通に計算しようとすると大きなメモリーが必要になるということです。
Running σ の場合、「過去の全データを使って」ということは、全ての入力を保存しておかなければならないのでしょうか?
できれば直前の値だけから算出したいですね。
平均・分散を逐次的に求める
まず、平均 μ・分散 σ^2の定義式を見てみましょう。
サンプル数 N 時点の平均・分散は、時系列入力 x について以下のように定義されます。
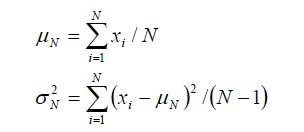
これを見るとまず平均は、新規データ x(N) 、データ数 N 、一つ前の平均値 μ(N-1)があれば、以下の式で逐次的に求められることがすぐ分かります。
![]()
過去の全データを持っておく必要はありません。
分散はどうでしょう?
上の式のままだと、Σ の中に ( x(i) - μ(N) ) があるので全データが必要そうに見えます。
では、式変形してみましょう。
分散の定義式は
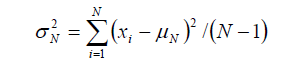
でした。これを展開すると
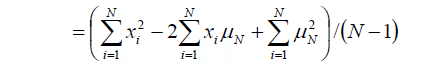
(N-1) までの和をくくり出して、
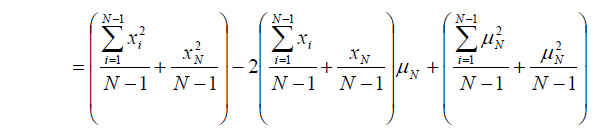
平均の定義式を使って整理すると、

ここで
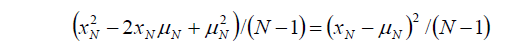
なので
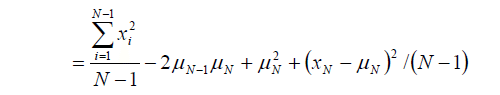
さらに (N-1) 時点の σ^2 をくくり出すために変形すると、
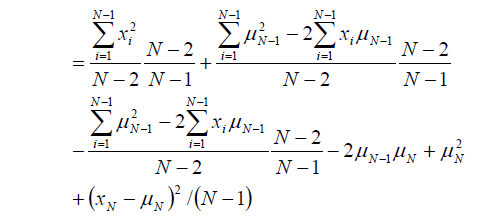
これを整理すれば、
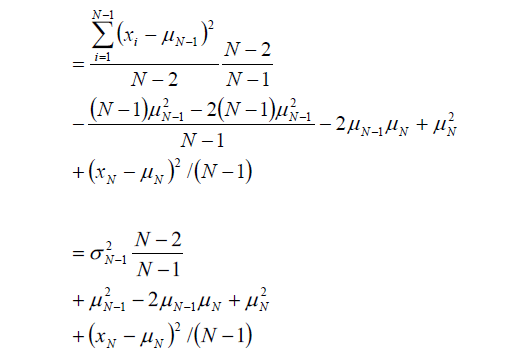
したがって分散も、新規データ x(N) 、データ数 N 、一つ前の分散 σ(N-1)^2があれば、以下の式で逐次的に求められることが分かりました。
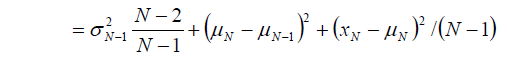
MATLAB Function ブロック
では、MATLAB Function ブロック に上で求めた式を入れて確認してみましょう。
Simulinkモデル全体としてはこのようになっています。
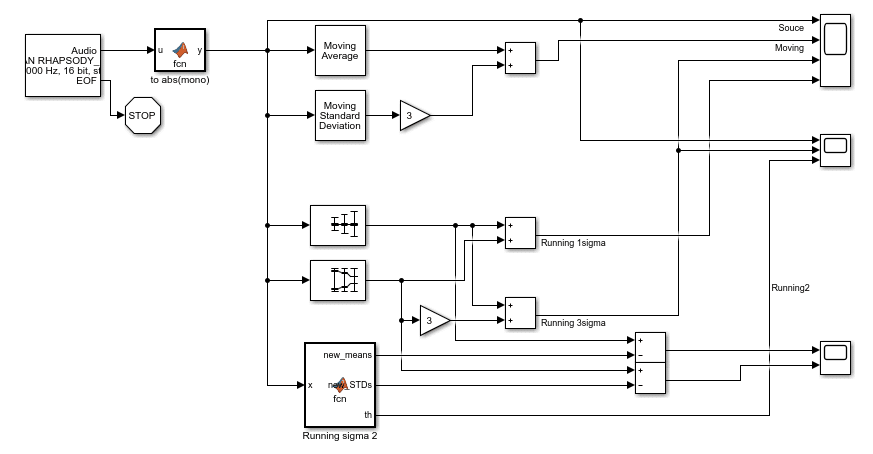
MATLAB Function ブロックをキャンバス上に配置、”Running sigma 2” と名前を付け、ダブルクリックしてエディター画面で以下のコードを書き、保存します。
function [new_means, new_STDs, th] = fcn(x)
persistent data_n old_mean old_var
if isempty(old_mean)
data_n = 1;
old_mean = 0;
old_var = 0;
new_means = zeros(size(x));
new_STDs = zeros(size(x));
th = zeros(size(x));
end
frameSize = length(x);
for k=1:frameSize
new_mean = (old_mean * (data_n-1) + x(k)) / data_n;
new_means(k) = new_mean;
if data_n > 1
new_var = old_var * (data_n-2)/(data_n-1) ...
+ (new_mean-old_mean)^2 ...
+ (x(k)-new_mean)^2 / (data_n-1);
else
new_var = 0;
end
new_STD = sqrt(new_var);
new_STDs(k) = new_STD;
th(k) = new_mean + 3*new_STD;
old_mean = new_mean;
old_var = new_var;
data_n = data_n + 1;
endpersistent は、永続変数の宣言です。
永続変数はこの関数内のローカル変数ですが、関数の呼び出し間で値が保持されます。初回呼び出し時は空なので、if isempty で初期化します。
N=1の時点では分散は定義されないので0を入れておきます。
MATLABは基本的にはフレーム単位の処理ですので、オーディオが1024サンプルずつ(デフォルト設定)入ってきてその単位で処理します。
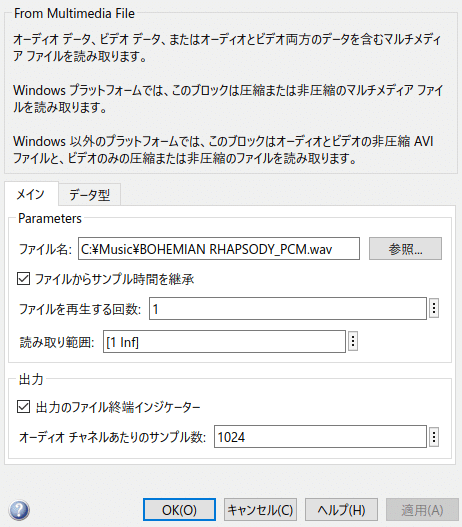
"From Multimedia File” ブロックの "オーディオ チャネルあたりのサンプル数" を "1" に設定すればサンプル単位でも動かすことができますが、MATLABの処理ブロックを使う場合、速度が極端に遅くなります。主な処理を全て MATLAB Functionブロック内に書いてしまう場合などは、サンプル単位でもリアルタイム動作が可能な場合もあります。(私はむしろこちらを使う方が多いですが)
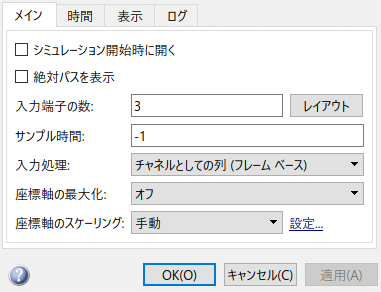
逆に、時系列グラフを表示する "Scope" はサンプル単位が標準なので、
右クリック -> コンフィギュレーション プロパティ -> メイン の "入力処理" を、"チャネルとしての列(フレームベース)" に設定しておきます。
ステレオオーディオ入力をモノラルに変換して abs 取る部分も、MATLAB Function で書いてしまった方が楽なので "to abs(mono)” と名前を付けて作ります。
function y = fcn(u)
y = abs((u(:,1) + u(:,2))/2);検証結果
Simulink の "Mean/Standard Deviation" ブロックを使った場合の結果と比較してみましょう。

グラフは綺麗に重なっています。
どうやら良さそうです。
エラーも見てみましょう。
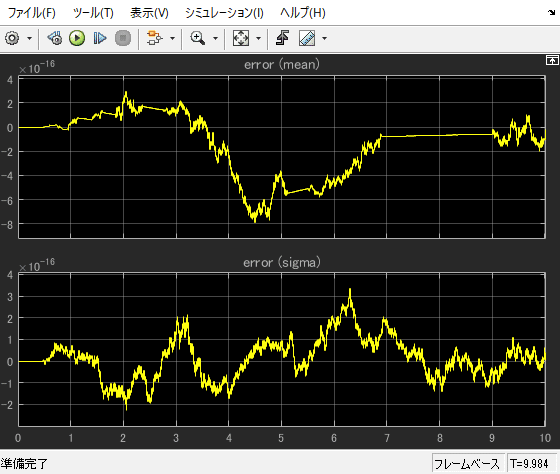
差分を見てみると、1e-16オーダーの誤差があるようです。
多少計算方法が違うのでしょうか?
まあ、極わずかな誤差なので、良しとしましょう!
(理由がお分かりの方は教えてください m(_ _)m )
このように、
-Simulink でアルゴリズム検証
-MATLAB Function で置き換え
-Simulink ブロックとの差を確認
-そのスクリプトを元にC等に書き換えて組込系へ
持って行くと、開発がとてもスムーズです。
MATLAB Functionブロックを使うと、Simulink の自由度が格段にアップしますし、組込系へ持って行くときに楽なので、お使いでない方は活用されてみてはいかがでしょうか?
この記事が気に入ったらサポートをしてみませんか?
