非平衡メモ
言葉
緩和:非平衡 → 平衡
ゆらぎには、遅い変化と速い変化がある。
ランジュバン方程式
ランジュバン方程式は不規則な運動を記述するのに適している。
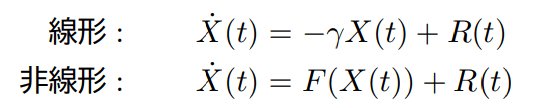
Ex 線形 )ブラウン運動のEOM(線形ランジュバン方程式)
mV^・(t) = - λ V (t) + R (t)
ただし、R (t) は ランダム力であり、撃力なので R (t) ∝ δ (t-t_0) 。
ランダム力のアンサンブル平均はゼロで、他の時間との相関もゼロである。
Ex 非線形) レーザートラップされた水中のコロイド粒子(非線形〃)
0 = λX^・(t) - ∇u(X) + R(t)
微小質量時で力はゼロ。0 = (水の抵抗) + (レーザーによるポテンシャル勾配) + (ランダム力)
フォッカー・プランク方程式(FP方程式)
FP方程式は非線形ランジュバン方程式と等価である。
FP方程式は、いくつかの仮定の基で、一度差分化された「非線形ランジュバン方程式」を、任意関数の「平均値の方程式」に代入することで得られる。(厳密には仮定と併せて等価ということ。)
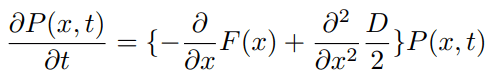

FP方程式は、例えばブラウン運動における位置の分布関数が時間経過と伴に広がっていく様子をよく表現できる。もちろん、レーザートラップされた水中のコロイド粒子の描像も記述できる。
第2種揺動散逸定理(2nd FDT)
2nd FDT は P, F, D の間の関係を与える。
2nd FDT を
・ブラウン運動 に応用すると アインシュタインの関係式
・ホワイトノイズ に応用すると ナイキストの定理
が得られる。
<第2種揺動散逸定とは>
X=X(t) がランジュバン方程式に従い、
かつ、FP方程式と等価なための条件を満たしており、
第一式のようなFP方程式の平衡解 P_eq(x) が存在するとき第二式が言える。
第二式は、F(x)がS(x)により決定されることを意味する。
特に、F(x)=L dS(x)/dx、つまり、X^・= L dS(X)/dx + R(t) のとき
L=D/2
が成り立つ。これが第2種揺動散逸定理。
なお、第二式は連続の式とFP方程式を設定したいくつか仮定のもとで変形することにより得られる。
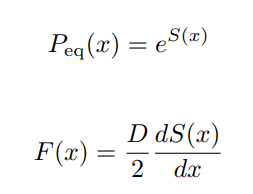
(ここまで、R5/02/23 時点)
Ex1 ) 微粒子
多くの物理系、特に微粒子系は、
t→∞ で 速度分布P(v)がマクスウェル分布になるという特徴をもとに、
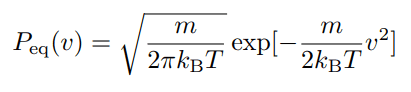
2nd FDT を用いて、Einsteinの関係式を導出する。
マクスウェル分布は、P_eq(v)=exp{S(v)} の S を
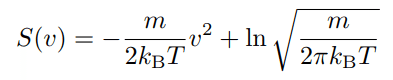
としたものである。
2nd FDTの左辺である F は速度に比例する抵抗であり、
右辺は上式のSをvで微分した値である。
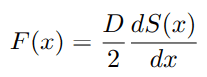
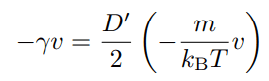
あとは、ランジュバン方程式において置いた定義式

を代入して整理すれば、Einsteinの関係式が導ける。
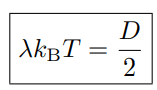
なお、各文字はそれぞれ λ:散逸(抵抗)、k_bT:平衡分布、D:揺動(ゆらぎの大きさ) に由来する。
「揺動」が「散逸」とつり合い、「平衡」しているのだ。
(ここまで、R5/03/01 時点)
Ex2 ) ホワイトノイズ
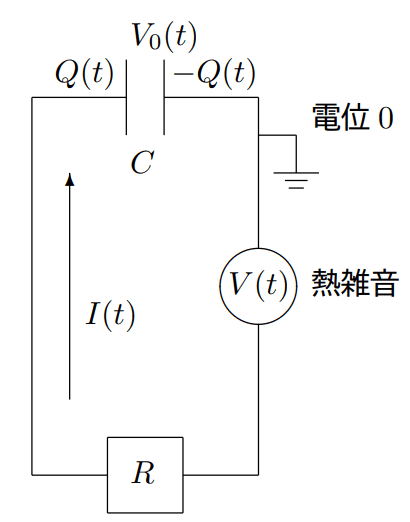
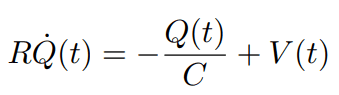
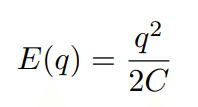
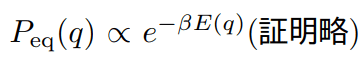
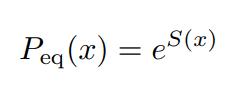
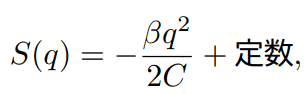
一方、線形ランジュバン方程式より
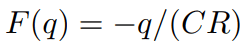
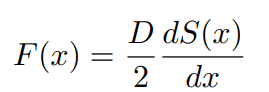
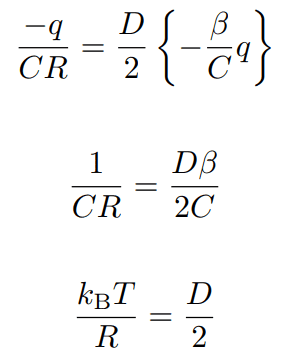
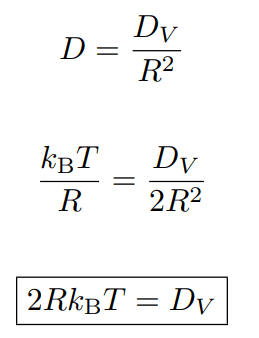
最後の四角で囲われた式は、ナイキストの定理という。
なお、各文字はそれぞれ R:散逸(電気抵抗)、k_bT:平衡分布、Dv:揺動(電圧ゆらぎの大きさ) 。
「揺動」が「散逸」とつり合い、「平衡」しているのだ。

(ここまで、R5/03/04 時点)
参考 下記サイトで学び、式の画像はこちらから引用させてもらいました。
今後もこのサイトで少しずつ学ばせてもらいます。
http://bussei.gs.niigata-u.ac.jp/~yoshimori/Hn18note.pdf
この記事が気に入ったらサポートをしてみませんか?
