気象データと機械学習を用いた電力需要予測
はじめに
小さい頃、桜といえば開花が卒業式の頃で、入学式の頃には散っている印象だったのが、近頃は3月上旬にはもう開花していたりと、気候変動の影響をじんわりと感じ始めている。
一方電力価格の上昇についてのニュースをよく見かけるようになり、気休めの節電努力をしている。
毎年劇的に気温が変動するわけではないが、1898年以降気象庁による正偏差が大きかった年1〜5位が2020年、2019年、2021年、2022年、2016年と近年に固まっていることを考えると、今後どんどん気温が変化するにつれ、電力需要も変化するのではないかと考えた。
そこで、機械学習を用いて、気象データを説明変数として電力需要予測ができないかと考え、以下のモデルを作成した。
実行環境
機械: iMac Intel Core i5 2019
言語: Python 3.9.16
実行: Google Colab
分析手順
①データの取得
②データの前処理
③モデルの構築/予測
④精度向上の試行
⑤汎化性能の評価
①データの取得
気象データ
データ源:気象庁の過去の気象データ・ダウンロードサイト
データの範囲:東京電力エリアである、東京都、神奈川県、埼玉県、千葉県、栃木県、群馬県、茨城県、山梨県、静岡県(富士川以東)の各都/県について、最も人口の多い地点を選んだ。
結果として、東京、横浜、千葉、さいたま、宇都宮、水戸、前橋、甲府、三島の九地点を選択した。
データの期間:2022年の時別値を指定した。
データの種類:気温、風速、相対湿度を選択した。
理由としては、体感温度に影響を与える主な要素が上記三つ+熱放射であり、熱放射と相関の高い全天日射量が県によっては丸ごとデータが欠損していたため、データの種類を上記三つに留めた。
なお一度にダウンロードできるデータに制限があったため、手作業で各データをダウンロードし、ファイルを結合したものをGoogle Driveにアップロードすることで利用可能としている。
電力データ
データ源:東京電力の過去の電力使用実績データサイトから直接csvファイルがダウンロードできるため、以下に示すコードで直接取得している。
データの期間:2022年(デフォルトで時別値)
実際のコード
import pandas as pd
import numpy as np
import datetime as dt
import math
import matplotlib.pyplot as plt
weather_df = pd.read_csv('/content/drive/MyDrive/aidemy_electricity/AllData_treated.csv')
elec_df = pd.read_csv('http://www.tepco.co.jp/forecast/html/images/juyo-2022.csv', encoding="shift_jis", skiprows=2)

②データの前処理
気象データ
欠損値を確認し、適宜削除・補完を行なう。
また、電力データと結合するために日時情報を抽出し新たなカラムを作成する。
# 8760行以降NaNとなっていたため、整理する
weather_df = weather_df.drop(weather_df.index[8759:])
# 欠損値を確認する
print(weather_df.isnull().sum())
# 欠損値が確認されたため補完する
weather_df = weather_df.fillna(method="ffill")
# indexを日時とする
weather_df.index = weather_df.index.map(lambda x: dt.datetime.strptime(weather_df.loc[x].Date, "%Y/%m/%d %H:%M"))
# DateとTimeとそれぞれの列を作る
weather_df[["Date","Time"]] = weather_df["Date"].str.split(' ', 1, expand=True)
# 月データの取得
weather_df["month"] = weather_df.index.month
# 曜日データの取得
weather_df["weekday"] = weather_df.index.weekday
# 時間データの取得
weather_df["hour"] = weather_df.index.hour
電力データ
電力データについても、後々結合するためにデータを整える。
# 列名を変換
elec_df.columns = ["Date","Time","kW"]
# 日付と時間のデータが分かれているので、一つにつなげて日時型に変換し、インデックスに指定
elec_df.index = elec_df.index.map(lambda x: dt.datetime.strptime(elec_df.loc[x].Date + " " + elec_df.loc[x].Time,"%Y/%m/%d %H:%M"))
# 月データの取得
elec_df["month"] = elec_df.index.month
# 曜日データの取得
elec_df["weekday"] = elec_df.index.weekday
# 時間データの取得
elec_df["hour"] = elec_df.index.hour気象データと電力データの結合
# 結合する
kw_df = pd.merge(elec_df, weather_df, on =["Date", "Time", "hour", "month", "weekday"], how = "outer")
# NaNを削除する
kw_df = kw_df.dropna()データの加工
# 説明変数の選択
X_cols = ['Chiba_humidity', 'Chiba_temp', 'Chiba_wind', 'Kofu_humidity',
'Kofu_temp', 'Kofu_wind', 'Maebashi_humidity', 'Maebashi_temp',
'Maebashi_wind', 'Mishima_humidity', 'Mishima_temp', 'Mishima_wind',
'Mito_humidity', 'Mito_temp', 'Mito_wind', 'Saitama_humidity',
'Saitama_temp', 'Saitama_wind', 'Tokyo_humidity', 'Tokyo_temp',
'Tokyo_wind', 'Utsunomiya_humidity', 'Utsunomiya_temp',
'Utsunomiya_wind', 'Yokohama_humidity', 'Yokohama_temp',
'Yokohama_wind']
# 目的変数の選択
y_cols = ["kW"]
# データの取得
X = kw_df[X_cols].values
y = kw_df[y_cols].values③モデルの構築/予測
i) 最も基礎的な決定木回帰モデルを用いる
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
# 学習データと検証データに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 決定木回帰モデル
model = DecisionTreeRegressor()
model.fit(X_train, y_train.ravel())
# 検証データの決定係数
print("決定木回帰:{}".format(model.score(X_test,y_test.ravel())))精度予測の指標には決定係数を用いる。
決定木回帰モデルによる決定係数は0.486であった。
ii) アンサンブル学習の一種であるランダムフォレスト回帰モデルを用いる
#学習データと検証データに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# ランダムフォレスト回帰モデル
model = RandomForestRegressor()
model.fit(X_train, y_train.ravel())
# 検証データの決定係数
print("ランダムフォレスト回帰: {}".format(model.score(X_test,y_test.ravel())))ランダムフォレスト回帰モデルによる決定係数は0.766となり、決定木と比較して0.280向上した。
ランダムフォレスト回帰モデルは複数の決定木回帰モデルを作り、結果を多数決で決める手法であり、決定木よりも高い予測精度が期待できるため、期待に沿った結果となっている。
④精度向上の試行
i) 時間に関する特徴量を追加する
説明変数に月、曜日、時間を追加し、以下に変更する。
# 月、週、時間を特徴量として追加する
X_cols = ['month', 'weekday', 'hour', 'Chiba_humidity', 'Chiba_temp', 'Chiba_wind', 'Kofu_humidity',
'Kofu_temp', 'Kofu_wind', 'Maebashi_humidity', 'Maebashi_temp',
'Maebashi_wind', 'Mishima_humidity', 'Mishima_temp', 'Mishima_wind',
'Mito_humidity', 'Mito_temp', 'Mito_wind', 'Saitama_humidity',
'Saitama_temp', 'Saitama_wind', 'Tokyo_humidity', 'Tokyo_temp',
'Tokyo_wind', 'Utsunomiya_humidity', 'Utsunomiya_temp',
'Utsunomiya_wind', 'Yokohama_humidity', 'Yokohama_temp',
'Yokohama_wind']こちらで上記同様にランダムフォレスト回帰を実行したところ、決定係数が0.955となった。
精度がかなり高くなり、時間や時期が電力需要予測に大きく影響していることがわかった。
ii) 風速データを離散化し新たな特徴量として追加する
すでにかなり高い精度が出力されているが、さらに精度を上げる方法として、外れ値の処理を行なった。
気象データの各カラムに対し箱ひげ図を出力したところ、全ての地点において、風速に外れ値が多数あることが確認できた。
# 外れ値確認のために箱ひげ図作成する
for column in weather_df.iloc[:, 1:].columns:
fig, ax = plt.subplots()
weather_df.boxplot(column=[column])
plt.show()
外れ値があることで学習が進みづらくなってしまうため、風速値に関しては、箱ひげ図で表される1/4分位数、2/4分位数(中央値)、3/4分位数、最大値を基準に、値を離散化した。具体的には以下のように離散化した。
0.0-1/4分位数の値: 1
1/4分位数-中央値: 2
中央値-3/4分位数: 3
3/4分位数-最大値: 4
離散化し新たに生成されたデータには"地点名"+"wind_level"というカラム名を与えた。
cities = ['Tokyo', 'Chiba', 'Kofu', 'Maebashi', 'Mishima', 'Mito', 'Saitama', 'Utsunomiya', 'Yokohama']
# 初期化する
for city in cities:
kw_df[city + '_wind_level'] = 0
# 風速値を離散化させる
for city in cities:
col_name = city + '_wind'
col_level_name = city + '_wind_level'
kw_df.loc[(kw_df[col_name] >= 0.0) & (kw_df[col_name] <= kw_df[col_name].describe()["25%"]), col_level_name] = 1
kw_df.loc[(kw_df[col_name] > kw_df[col_name].describe()["25%"]) & (kw_df[col_name] <= kw_df[col_name].describe()["50%"]), col_level_name] = 2
kw_df.loc[(kw_df[col_name] > kw_df[col_name].describe()["50%"]) & (kw_df[col_name] <= kw_df[col_name].describe()["75%"]), col_level_name] = 3
kw_df.loc[(kw_df[col_name] > kw_df[col_name].describe()["75%"]) & (kw_df[col_name] <= kw_df[col_name].describe()["max"]), col_level_name] = 4

これまでの説明変数から連続値である風速値を削除し、離散化した風速値を代わりに追加した。
X_cols = ['month', 'weekday', 'hour', 'Chiba_humidity', 'Chiba_temp', 'Kofu_humidity',
'Kofu_temp', 'Maebashi_humidity', 'Maebashi_temp',
'Mishima_humidity', 'Mishima_temp',
'Mito_humidity', 'Mito_temp', 'Saitama_humidity',
'Saitama_temp', 'Tokyo_humidity', 'Tokyo_temp',
'Utsunomiya_humidity', 'Utsunomiya_temp', 'Yokohama_humidity', 'Yokohama_temp',
'Yokohama_wind', "Chiba_wind_level", "Tokyo_wind_level",
"Yokohama_wind_level", "Utsunomiya_wind_level", "Saitama_wind_level",
"Mito_wind_level", "Mishima_wind_level", "Maebashi_wind_level", "Kofu_wind_level"]これまで同様にランダムフォレスト回帰モデルを用いたところ、決定係数は0.957と値が微増した。
iii) 異なるアンサンブル学習器を利用する
ランダムフォレスト回帰とは異なる決定木のアンサンブル学習器である、HistGradientBoostingRegressorを用いた。
ランダムフォレスト回帰ではランダムに決定木を組み合わせる一方、HistGradientBoostingRegressorは逐次的に決定木モデルを学習し、前の決定木モデルのエラーを修正するモデルである。ランダムフォレスト回帰と比較して、用いるモデルの数が少ないため処理時間が短いという特徴がある。
from sklearn.ensemble import HistGradientBoostingRegressor
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
#HistGradientBoostingRegressorモデル
model = HistGradientBoostingRegressor()
model.fit(X_train, y_train.ravel())
# 検証データの決定係数
print(model.score(X_test,y_test.ravel()))上記の離散化された風速値、および時間に関する特徴量を説明変数とし、HistGradientBoostingRegressorを回したところ、決定係数は0.963となった。
⑤汎化性能の評価
工夫を重ねた結果、決定係数が0.963というかなり高い精度のモデルを作成することができた。
あまりにも精度が高いため、ほかのデータに対しても汎化性能があるのか、過学習などを起こしているのか確認するため、2021年の気象データを上記で作成したHistGradientBoostingRegressorモデルに学習させた結果を評価することにする。
データの取得・前処理
2022年の気象データと同様のデータ加工を、2021年の気象データに施した。
#データの読み込み、欠損値の処理
weather21_df = pd.read_csv('/content/drive/MyDrive/aidemy_electricity/alldata_treated2021.csv')
weather21_df = weather21_df.drop(weather21_df.index[8759:])
weather21_df = weather21_df.fillna(method="ffill")
# indexを日時とする
weather21_df.index = weather21_df.index.map(lambda x: dt.datetime.strptime(weather21_df.loc[x].Date, "%Y/%m/%d %H:%M"))
# DateとTimeとそれぞれの列を作る
weather21_df[["Date","Time"]] = weather21_df["Date"].str.split(' ', 1, expand=True)
# 月データの取得
weather21_df["month"] = weather21_df.index.month
# 曜日データの取得
weather21_df["weekday"] = weather21_df.index.weekday
# 時間データの取得
weather21_df["hour"] = weather21_df.index.hour
# 風速値の離散化
cities = ['Tokyo', 'Chiba', 'Kofu', 'Maebashi', 'Mishima', 'Mito', 'Saitama', 'Utsunomiya', 'Yokohama']
# 初期化する
for city in cities:
weather21_df[city + '_wind_level'] = 0
# 風速値を離散化させる
for city in cities:
col_name = city + '_wind'
col_level_name = city + '_wind_level'
weather21_df.loc[(weather21_df[col_name] >= 0.0) & (weather21_df[col_name] <= weather21_df[col_name].describe()["25%"]), col_level_name] = 1
weather21_df.loc[(weather21_df[col_name] > weather21_df[col_name].describe()["25%"]) & (weather21_df[col_name] <= weather21_df[col_name].describe()["50%"]), col_level_name] = 2
weather21_df.loc[(weather21_df[col_name] > weather21_df[col_name].describe()["50%"]) & (weather21_df[col_name] <= weather21_df[col_name].describe()["75%"]), col_level_name] = 3
weather21_df.loc[(weather21_df[col_name] > weather21_df[col_name].describe()["75%"]) & (weather21_df[col_name] <= weather21_df[col_name].describe()["max"]), col_level_name] = 4
電力データも2022年同様に読み込む。
# 電力データの読み込み
elec2021_df = pd.read_csv('http://www.tepco.co.jp/forecast/html/images/juyo-2021.csv', encoding="shift_jis", skiprows=2)
# 列名を変換
elec2021_df.columns = ["Date","Time","kW"]
# 気象データに合わせて1:00スタートとするため、最初の行を削除する
elec2021_df = elec2021_df.drop(elec2021_df.index[0])モデルの構築
説明変数と目的関数として、X_2021とy_2021を定義する。
X_colsにはこれまで同様に、月、曜日、時間および離散化した風速値+そのほかの気象データを指定している。
y_colsも電力である"kW"を指定している。
X_2021 = weather21_df[X_cols].values
y_2021 = elec2021_df[y_cols].values改めて、2022年のデータを用いてHistGradientBoostingRegressorモデルを作成する。作成したモデルに、2021年のデータを入力し汎化性能を確認する。
from sklearn.ensemble import HistGradientBoostingRegressor
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
#HistGradientBoostingRegressorモデル
model = HistGradientBoostingRegressor()
# 検証データでモデルを作成
model.fit(X_train, y_train.ravel())
# 検証データの決定係数
train_score = model.score(X_train, y_train.ravel())
# 学習データの決定係数(過学習していないかの確認)
test_score = model.score(X_test, y_test.ravel())
# 2021年データの決定係数
test2021_score = model.score(X_2021,y_2021)
print("HistGradientBoostingRegressor・学習データの決定係数: {}".format(train_score))
print("HistGradientBoostingRegressor・検証データの決定係数: {}".format(test_score))
print("HistGradientBoostingRegressor・2021データの決定係数: {}".format(test2021_score))結果は以下の通りとなった。
学習データの決定係数: 0.983
検証データの決定係数: 0.963
2021データの決定係数: 0.927
考察
2021年および2022年の検証データを用いた予測値と実値を比較した図を作成する。
import matplotlib.pyplot as plt
y_pred2022 = model.predict(X_test)
y_pred2021 = model.predict(X_2021)
# サブプロットを作成
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# 2021年の実際の値と予測値をプロット
ax1.scatter(y_2021, y_pred2021, alpha=0.5, s=10)
# 決定係数=1となるような理想的な線を参考として引く
lims = [np.min([ax1.get_xlim(), ax1.get_ylim()]), np.max([ax1.get_xlim(), ax1.get_ylim()])]
ax1.plot(lims, lims, color='red', linestyle='--')
ax1.set_xlabel('Actual Value')
ax1.set_ylabel('Predicted Value')
ax1.set_title('Actual vs. Predicted Values (2021)')
# 2022年の実際の値と予測値(検証データ)をプロット
ax2.scatter(y_test, y_pred2022, alpha=0.5, s=10)
# 決定係数=1となるような理想的な線を参考として引く
lims = [np.min([ax2.get_xlim(), ax2.get_ylim()]), np.max([ax2.get_xlim(), ax2.get_ylim()])]
ax2.plot(lims, lims, color='red', linestyle='--')
ax2.set_xlabel('Actual Value')
ax2.set_ylabel('Predicted Value')
ax2.set_title('Actual vs. Predicted Values (2022)')
# グラフを表示
plt.show()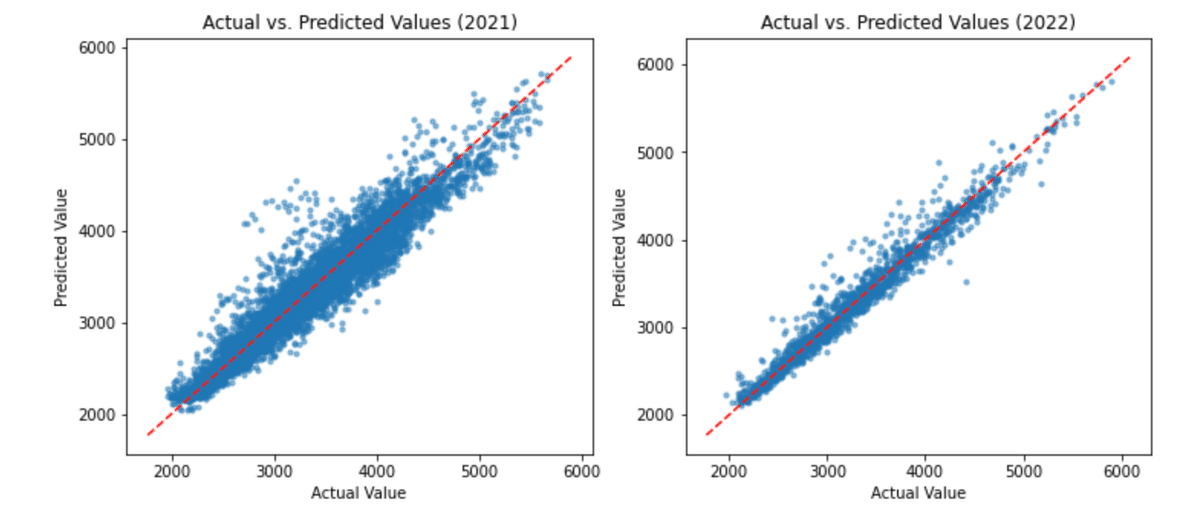
2021年、2022年どちらにおいても全体的には対角線上にプロットされており、良い結果が得られていることがわかるが、2021年のほうが相対的にばらつきが多いことが確認できる。
考えられる大きな理由の一つとしては、2021年のデータには2022年と比較して、欠損値が多くあることが挙げられる。特に、さいたまの湿度に関しては半年分以上のデータが欠損している。


2021年については、データの外れ値などデータの特性を観察せずに2022年と同様の扱いをしているため、データの特性にあったデータ加工をすればさらによい予測結果が得られるかもしれない。
まとめ
今回は、気象データである代表地点の気温、風速、相対湿度およびから電力需要予測モデルを構築することを試みた。
各モデル予測試行のまとめを以下の表に示す。

気象データを説明関数として利用したいと思った理由は、エアコンの利用や冷却器、ヒーターなど、気温の変化によって電力需要の変化が観測できると考えたからである。
エネルギー白書2022によると、2020年度における部門別電力最終消費の内訳としては、産業が36%、業務他が33%、家庭が29%、運輸が2%となっている。
産業や業務においては動力や照明、家庭においては照明や冷蔵庫の利用など、気温の変化とあまり関係のない電力需要も多数考えられることから、今回、気象データおよび時間データのみでこれほどの精度が出せるとは思っていなかった。
特に時間に関するデータである月、曜日、時間を特徴量として追加したことにより、決定係数が0.3近く上がったことから、時間と電力需要には高い相関があることが確認できた。
また2022年の学習データと検証データから作成したHistGradientBoostingRegressorモデルを用いて、2021年の気象・時間データをもとに予測した電力需要も高い精度が得られ、汎化性能もあるモデルと言えるかと思う。今後の課題としては、パラメータチューニングを行うことや、時系列解析との結果を比較することが挙げられる。
初めて機械学習の予測モデルを作成してみたが、モデルの選択一つで結果がかなり改善したり、データ加工の方法を勉強することができ、とても良い経験になりました。
参考文献
・気象庁. 「日本の年平均気温偏差の経年変化(1898〜2022年)」
https://www.data.jma.go.jp/cpdinfo/temp/an_jpn.html, (参照 2023-03-25)
・@mix_dvd.「機械学習で電力需要を予測してみる パート2」
https://qiita.com/mix_dvd/items/1f96f5202614dbea93e0, (参照 2023-03-25)
・片桐 智志,「10.1 どの分類モデルを選ぶべきか」https://fan-adn.github.io/ist-textbook-open/classif-theory.html, (参照 2023-03-25)
・Jason Brownlee. "Histogram-Based Gradient Boosting Ensembles in Python". https://machinelearningmastery.com/histogram-based-gradient-boosting-ensembles/., (参照 2023-03-25)
・経済産業省 資源エネルギー庁, 「令和3年度エネルギーに関する年次報告(エネルギー白書2022)」https://www.enecho.meti.go.jp/about/whitepaper/2022/, (参照 2023-03-25)
この記事が気に入ったらサポートをしてみませんか?
