
機械系大学院入試のための備忘録
ここでは,機械系大学院入試の主要試験科目である四力において重要となる考え方や,具体的な問題の解き方を自分なりの言葉で書き下しまとめてみる.試験直前の自分自身へ向けたものであるが,これから機械系大学院入試を受ける受験生の方にもぜひ参考にしていただきたい.
はじめに
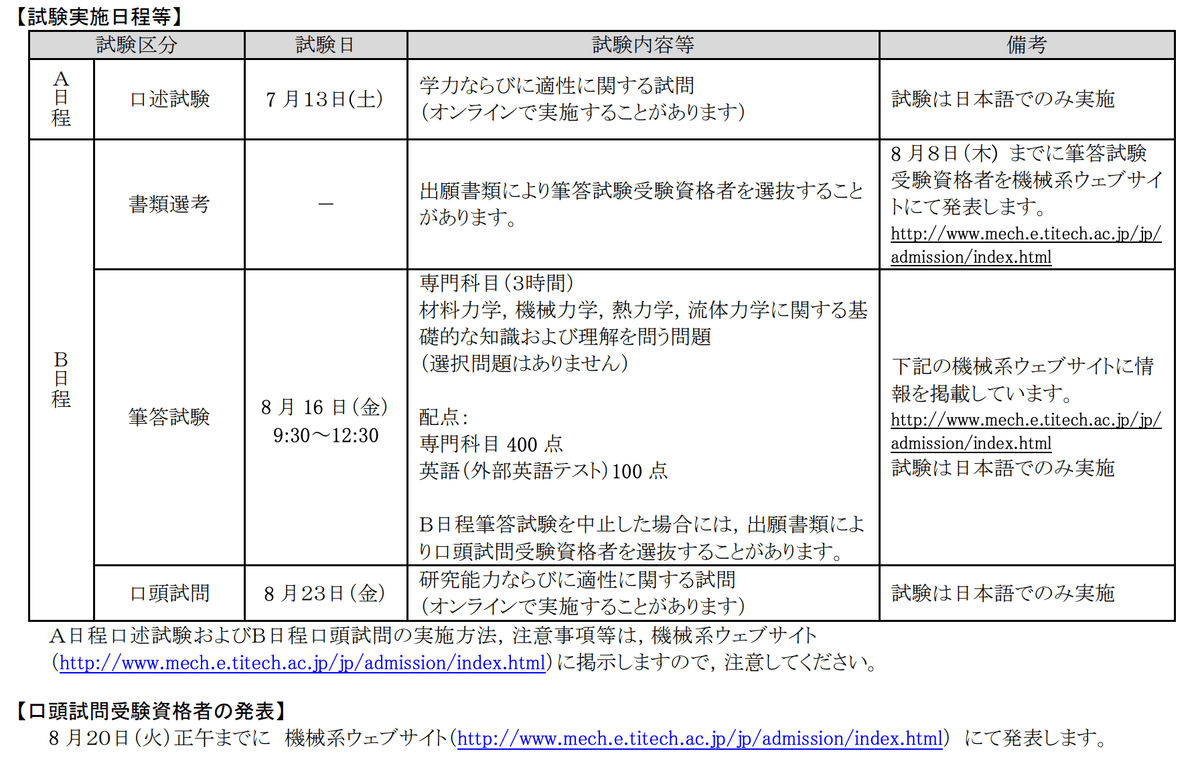
東工大の機械系大学院入試における専門科目の試験時間は以下の通りである.
四力 180分(45分×4)100点×4
四力のひと科目あたりの時間が45分と短く,普段から時間を意識して勉強するほうが良いように思う.また,ある程度の暗記事項を作成しておき,導出の時間は設けないようにしたほうがよい.
以下作戦.
1.熱力学は最も時間を短縮できる科目.単に知識を問うだけの問題も多く,幅広い暗記が必要であるが,分からないものは考えても分からないので時間を意識すること.最初に解くか?
2.材料力学は解法がきっちりと定まっていて,演習を積めば手が止まることは無いはず.やることをしっかりとやる.こちらも単に知識を問う問題があるが,考えすぎないこと.暗記事項(ex.特定の荷重,モーメントに対するはりのたわみ,他導出するまでもないもの)を増やすことで解答時間の短縮を図る.
3.機械力学も材力と同様の印象.手を止めたくない.知識問題も存在.運動方程式立てれたら勝ち(回転の運動方程式ちゃんと復習)
4.流体力学.東工大の問題は誘導が丁寧な印象を受けるので,解けないことはない.他科目と比べて計算に時間がかかる恐れや,雪崩れてしまう危険性から最後に解くのが賢明か.
全体を通して誘導が丁寧な問題が多い印象.
1. 材料力学
JSMEテキストで知識を補充していく.単語の穴埋めもここからが中心.
材料力学は問題に対して比較的手を動かしやすく,「やるだけ」のような問題も多い.慣れていないと計算に時間をとられてしまうので,踏み入ったところまで暗記をしてもいいかも.
⚠️はりの問題でのせん断力,モーメントは以下の向きを正とする.

1.1 材料力学の基礎(知識問題)
平面応力状態は2つの垂直応力成分と1つのせん断応力成分で表される.平面応力状態の薄板材内部に任意の傾斜面を考える.この傾斜面に作用している垂直応力とせん断応力は傾斜面の角度の関数となり,垂直応力のみが生じて,せん断応力が0となる面を主応力面と呼び,このときの垂直応力を主応力と呼ぶ.また,せん断応力が最大値となる面を主せん断応力面と呼び,主応力面と主せん断応力面のなす角は45度となる.(R5)
低炭素鋼:応力の増加とともに明らかな降伏現象が見られ,このとき,引張試験片の平行部の一部にすべり線が生じ,その後,ほぼ一定の応力を保ちながらこの線が引張試験片の平行部に広がる.このときの応力は下降伏点となる.平行部がすべて弾性変形した後に荷重が再び上昇するが,この現象を加工硬化という.(R4)
応力-ひずみ曲線における最大の応力を引張強さと呼ぶ.はりに曲げモーメントを負荷し,塑性変形が生じたのちに除荷を行うと,はりには残留応力が発生する.(R3)
せん断応力のみが負荷している状態→純せん断
鋳鉄のようにほとんど変形せずに破壊に至る材料を脆性材料という.
(R1)
S45C→降伏がみられて,よく見る感じの応力ひずみ線図.S45Cの応力ひずみ線図において,原点から比例限度までの傾きをヤング率といい,降伏の際の極大値を上降伏点,極小値を下降伏点という.引張強さ以降では,試験片に局所的なくびれが生じる.(H31)
計算ミスチェック
$$
\dfrac{dM(x)}{dx}=V(x)
$$
1.2 棒の引張・圧縮応力・熱応力
棒の引張・圧縮問題に限らず,材料力学の試験問題においてまず最初にすることは,自由体図(Free Body Diagram)を描くこと.対象物体にかかっている力,モーメントを図に描き起こして,その状況を把握することが大切.
フックの法則
$$
\sigma = E \varepsilon
$$
平面応力状態でのフックの法則
$$
\varepsilon_x=\dfrac{1}{E}(\sigma_x-\nu \sigma_y) \\
\varepsilon_y=\dfrac{1}{E}(\sigma_y-\nu \sigma_x) \\
\varepsilon_z=-\dfrac{\nu}{E}(\sigma_x+\sigma_y)
$$
伸び
$$
\varDelta l = \dfrac{Fl}{EA}
$$
熱膨張
$$
\Delta L = \alpha L \Delta T
$$
温度分布が位置$${x}$$に依存する場合(初期温度$${T_0}$$)
$$
\Delta L = \alpha \int_{0}^{l} (T(x)-T_0) dx
$$
例題:H27問1(4)
(4)円菅下端から上向きに$${x}$$軸を取れば,温度分布は$${T(x)=T_0 + \dfrac{T_1-T_o}{L}x}$$となる.初期温度が$${T_0}$$であるから,温度変化は$${\varDelta T(x)=\dfrac{T_1-T_o}{L}x}$$となる.したがって,求める伸び$${\lambda_2}$$は$${\lambda_2=\alpha \int_{0}^{L}\dfrac{T_1-T_o}{L}xdx=\dfrac{\alpha(T_1-T_0)L}{2}}$$となる.
例題:R3(2022)問2
これが解ければ熱膨張問題は大丈夫.
1.3 はりの曲げ応力
断面二次モーメント
(軸からの距離)^2 × 微小面積 を断面全体で積分
・円
$$
I=\dfrac{\pi d^4}{64}
$$
・長方形
$$
I=\dfrac{bh^3}{12}
$$
曲げ応力
$$
\sigma=\dfrac{M(x)}{I}y
$$
さえ頭に入れておけばおk.
1.4 はりのたわみ
たわみの方程式は
$$
EI\dfrac{d^2y}{dx^2} = -M(x)
$$
上記のように書ける.各部位におけるモーメント分布を求めることでたわみの方程式が求まる.あとは,辺々積分したのちに境界条件を用いて具体的な定数の値を算出することで,各位置におけるたわみやたわみ角が得られる.ここで,$${M(x)}$$は最初に示した方向を正として,$${y}$$は下向きに取っている.境界条件は直感的に分かるよね.↓
固定端
$$
y=0 \\ y'=0
$$
回転支持
$$
y=0
$$
荷重が負荷されている箇所(B)
$$
y_{AB}=y_{BC} \\ y'_{AB}=y'_{BC}
$$
暗記事項
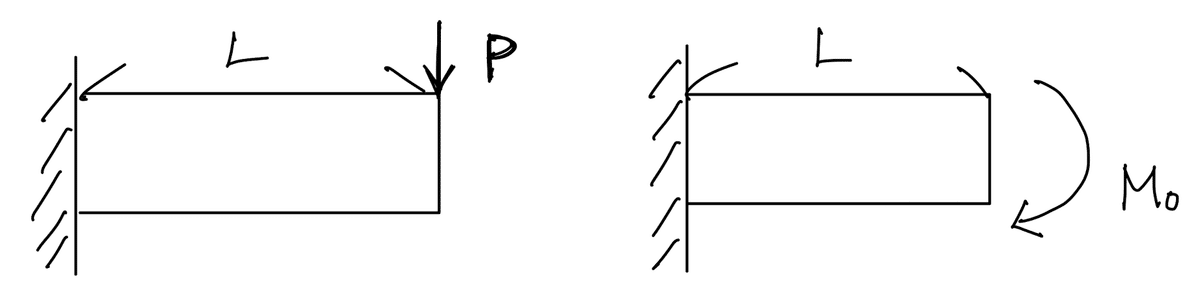
荷重$${P}$$が負荷しているとき
$$
y_{max}=y_{x=L}=\dfrac{PL^3}{3EI}
$$
$$
\theta_{max}=\theta_{x=L}=\dfrac{PL^2}{2EI}
$$
モーメント$${M_0}$$が負荷しているとき
$$
y_{max}=y_{x=L}=\dfrac{M_0L^2}{2EI}
$$
$$
\theta_{max}=\theta_{x=L}=\dfrac{M_0L}{EI}
$$
等分布荷重$${q}$$が負荷しているとき(一応覚えるか〜)
$$
y_{max}=y_{x=L}=\dfrac{qL^4}{8EI}
$$
$$
\theta_{max}=\theta_{x=L}=\dfrac{qL^3}{6EI}
$$
1.5 ねじり
・断面二次極モーメント
断面二次モーメントと同様な考えで,ある微小領域までの距離の2乗×微小領域の面積を断面全体で積分して得られる.軸からの距離ではなくて,断面中心からの距離の2乗×面素に注目?(中心を貫く軸回りの断面二次モーメントについて考えている)
円の断面二次極モーメントだけ覚えておけばよく,
$$
I_p=\dfrac{\pi d^4}{32}
$$
・ねじり関連の暗記事項
長さ$${L}$$,半径$${r}$$の丸棒にねじりモーメント$${T}$$が作用しているとき,せん断応力$${\tau}$$,せん断ひずみ$${\gamma}$$,比ねじれ角$${\theta}$$は以下の通りである.
$$
\tau = G\gamma = \dfrac{r}{I_p} T \\
\gamma = \dfrac{r}{G I_p} T \\
\theta = \dfrac{\gamma}{r} = \dfrac{1}{G I_p} T
$$
比ねじれ角は単位長さあたりのねじれ角であり,今回はねじれ角を$${L}$$で除した値となる.
1.6 モールの応力円
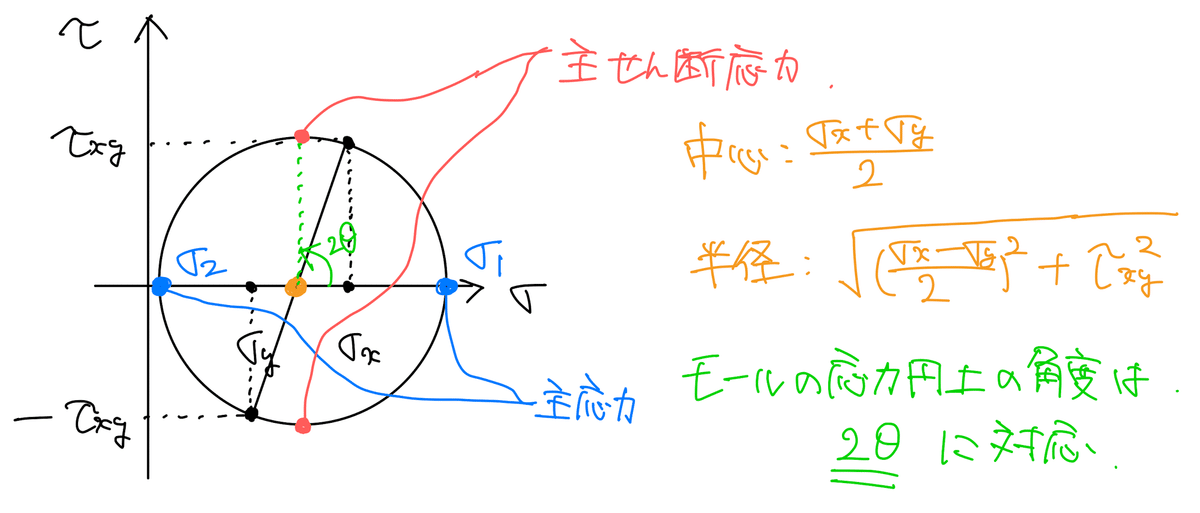
モールの応力円を表す式は,
$$
(\sigma - \dfrac{\sigma_x + \sigma_y}{2})^2 + \tau^2 = (\dfrac{\sigma_x - \sigma_y}{2})^2 + {\tau_{xy}}^2
$$
導出の過程は省略するが,以下の図でその意味を理解されたい.複合応力状態における主応力を求めるときにも使うことができて,非常に便利な道具である.
1.7 薄肉円筒(あんま出なさそう?)
圧力を受ける薄肉円筒

力の釣り合いから軸方向の応力を以下で得る.
$$
2\pi rt\sigma_z=\pi r^2p \therefore \sigma_z=\dfrac{pr}{2t}
$$

円周方向の応力については単位長さで一部分を抜き取って,力の釣り合いから,
$$
2pr=2t\sigma_t \therefore \sigma_t=\dfrac{pr}{t}
$$
上記より,円周方向に垂直な断面の応力は,軸方向に垂直な断面の応力の2倍となる.このため,円筒においては,側面が軸方向に沿って割けるような破壊が起こることが多い.
内圧を受ける薄肉球殻

円筒と同様に力の釣り合いを考えれば,
$$
2\pi rt\sigma_t=p\pi r^2 \therefore \sigma_t = \dfrac{pr}{2t}
$$
圧力から力を考えるときは,考えたい方向,軸に垂直な断面積を圧力に乗じればよい.(射影)
1.8 カスチリアーノの定理
全ひずみエネルギーを荷重で偏微分すると,その点でのたわみが得られるというもの.すごい
引張によるひずみエネルギー
$$
U_p=\int_{0}^{L}\dfrac{P^2}{2EA}dx
$$
軸のねじりによるひずみエネルギー
$$
U_t=\int_{0}^{L}\dfrac{T^2}{2GI_p}dx
$$
はりの曲げによるひずみエネルギー
$$
U_b=\int_{0}^{L}\dfrac{M^2}{2EI}dx
$$
カスチリアーノの定理
$$
\lambda_k=\dfrac{\partial U}{\partial P_k}
$$
荷重をモーメントで置き換えると,回転角が得られる.
$$
\theta_k=\dfrac{\partial U}{\partial M_k}
$$
例題:H27問2
カスチリアーノの使い方
1.9 座屈
最小座屈荷重$${P_c}$$のみ覚える.たわみは知りません.
$$
P_c=L \dfrac{\pi^2EI}{l^2}
$$
ここで,$${L}$$は端末条件係数であり,条件によって変化する.

2. 機械力学
7/23なう(試験25日前)ですが,危機感を持ち始めたので下記の参考書を買いました.(遅すぎ) 語彙,知識問題もこの参考書から出るっぽいので過去問と照らし合わせて埋めていきます.
基本的なマスばねダンパ系について,運動方程式を立てて解けるようにしておく.固有振動数や減衰比,2自由度系の共振の山のグラフなどは暗記しておく.2.1, 2.2は精選の内容.JSMEテキストで直前まで勉強しよう.
追記※7/29(月)
機力がいっちゃんムズイ.(H28の過去問に殴られて号泣)
もう分かるとこだけしっかり解こう.無理そうだったら他科目専念!
2.1 1自由度系の減衰自由振動
減衰要素を考慮した1自由度の減衰振動を考える.質点,線形ばね,速度比例形の減衰要素をもつ系の自由振動の運動方程式は,
$$
m\ddot{x}+c\dot{x}+kx=0
$$
である.これは次のように変形できる.
$$
\ddot{x}+2\zeta\omega_n\dot{x}+\omega_n^2x=0,\,\omega_n=\sqrt{\dfrac{k}{m}},\,\zeta=\dfrac{c}{c_c},\,c_c=2\sqrt{mk}
$$
ここで,$${\omega_n}$$は不減衰固有角振動数,$${\zeta}$$は減衰比,$${c_c}$$は臨界減衰係数である.減衰比の値は$${\zeta_c=1}$$を臨界値として後述のように減衰振動の特性を表す.式中$${x}$$は実数値であるが,変数を複素数まで広げることで表現が簡潔になるのでそれを試みる.ただし,実際の現象は,複素数の実部が表す.今,運動方程式の基本解を未定の複素定数$${A}$$および$${\lambda}$$を用いて,
$$
x=Ae^{\lambda t}
$$
の形で仮定し,これを運動方程式に代入すると,
$$
(\lambda^2+2\zeta\omega_n\lambda+\omega_n^2)Ae^{\lambda t}=0
$$
が得られるが,このとき$${A=0}$$は自明な解であるので,$${A\not = 0}$$のとき,すなわち,きちんと振動状態であるときの非自明解を考えると,$${0\le\zeta<1}$$のとき,
$$
\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0\to\lambda_{1,2}=-\zeta\omega_n\pm i\omega_d,\,\omega_d=\sqrt{1-\zeta^2}\omega_n
$$
を得る.ここで,$${\omega_d}$$は減衰固有角振動数であり,上の第一式を特性方程式または振動数方程式,その根を特性根とよぶ.このように,$${0\le\zeta<1}$$のとき,特性根は共役な複素根となる.今,運動方程式の一般解は基本解の線形結合で表され,その解は
$$
x=A_1e^{\lambda_1 t}+A_2e^{\lambda_2 t}=e^{-\zeta\omega_n t}(C\cos{\omega_d t}+D\sin{\omega_d t}) \\
=e^{-\zeta\omega_n t}X\cos{(\omega_d t-\phi)} \\
X=\sqrt{C^2+D^2}, \, \phi=\tan^{-1} \left( \dfrac{D}{C} \right)
$$
となる.この結果から,減衰比$${\zeta}$$の値に依る減衰振動の特性が見えてくる.$${\zeta=0}$$の場合は,一定の振幅を保ったまま振動をし続ける.一方,$${0<\zeta<1}$$の場合,解$${x}$$は時間経過によってゼロに漸近する指数関数と周期関数の積であるから質点はその振幅が徐々に小さくなりながら振動する.このような振動を減衰自由振動といい,$${0<\zeta<1}$$の状態を不足減衰とよぶ.なお,$${\zeta=1}$$の状態を臨界減衰,$${\zeta>1}$$の状態を過減衰とよび,いずれも特性根は負の実数となり,時間経過とともにゼロに単調に漸近する非振動的な解となる.
2.2 1自由度系の強制振動
線形ばねとダッシュポットで指示された質点に調和外力$${f\cos\varOmega t}$$が作用する,最も基本的な1自由度系の強制振動の運動方程式は,静的平衡からの質点の変位を$${x}$$とすると,次のようになる.
$$
m\ddot{x}+c\dot{x}+kx=f\cos\varOmega t
$$
また,各パラメータを用いて式を変形すると,
$$
\ddot{x}+2\zeta\omega_n\dot{x}+\omega_n^2x=x_{st}\omega_n^2\cos\varOmega t,\,x_{st}=\dfrac{f}{k}, \, \omega_n=\sqrt{\dfrac{k}{m}},\,\zeta=\dfrac{c}{2\sqrt{mk}}
$$
となる.特解を導出した後の重要な式のみまとめる.
$$
M_d=\dfrac{X}{x_{st}}=\dfrac{1}{\sqrt{\left(1-\dfrac{\omega^2}{\omega_n^2}\right)^2+{\left(2\zeta\dfrac{\omega}{\omega_n}\right)^2}}}=\dfrac{1}{\sqrt{\left(1-\eta^2\right)^2+{\left(2\zeta\eta\right)^2}}}
$$
$$
\eta=\dfrac{\omega}{\omega_n}
$$
$${M_d}$$は振幅比を表すパラメータであり,$${\eta}$$は振動数比である.振幅比,振動数比の関係を表したグラフを共振曲線,周波数応答曲線などとよぶ.共振曲線は減衰比$${\zeta}$$が小さいときには,$${\varOmega\approx\omega_n}$$で大きなピークをとり,この現象を共振とよぶ.また,$${\zeta}$$が小さいほどピーク値は大きく,$${\zeta=0}$$のときには$${\varOmega=\omega_n}$$で$${M_d}$$は無限大となる.
以下で共振曲線の例を見てみる.

ここで,$${\eta=1}$$で$${M_d}$$が最大とはならず,以下の共振周波数$${\omega_r}$$のとき,$${M_d}$$は最大となることに注意.
$$
\omega_r=\omega_n\sqrt{1-2\zeta^2}
$$
※$${\omega_r}$$は$${\omega_n}$$よりも小さい!
2.3 2自由度系の振動

減衰のない2自由度系について運動方程式を立てると,
$$
m_1 \ddot x_1 = f_1 - k_1x_1 - k_2(x_1-x_2) \\
m_2 \ddot x_2 = f_2 - k_3x_2 - k_2(x_2-x_1)
$$
$$
\Rightarrow \begin{pmatrix} m_1 & 0 \\ 0 & m_2 \end{pmatrix} \begin{pmatrix} \ddot x_1 \\ \ddot x_2 \end{pmatrix} + \begin{pmatrix} k_1+k_2 & -k_2 \\ -k_2 & k_2+k_3 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} f_1 \\ f_2 \end{pmatrix}
$$
つまり,
$$
\bm{M}\ddot{\bm{x}}+\bm{Kx}=\bm{f}
$$
のカタチで整理できる.
今,自由振動を考える.外力$${\bm{f}=\bm{0}}$$とおけば,運動方程式は,
$$
\bm{M}\ddot{\bm{x}}+\bm{Kx}=\bm{0}
$$
この自由振動の固有角振動数を$${\omega}$$,振幅を$${\bm{u}=(u_1,u_2)^\mathsf{T}}$$としてこれを求めてみる.
$$
\bm{x}=\bm{ue}^{i \omega t}
$$
とおいて,運動方程式に代入すれば,
$$
\begin{pmatrix} -{\omega}^2 \bm{M} + \bm{K} \end{pmatrix}\bm{u} = \bm{0}
$$
これが非自明解を持つためには,
$$
\begin{vmatrix} -{\omega}^2 \bm{M} + \bm{K} \end{vmatrix} = 0
$$
となればよい.上式を解けば固有角振動数を二つ得た後,二つの振幅比を得る.この振幅比は固有振動モードと呼ばれ,自由振動の状態において,系はある固有角振動数で特定のカタチの振動をおこなう.この特性をモード特性と呼ぶ.
自由振動の解は上記二つの固有振動モードの重ね合わせによって表すことができる.
強制振動も1自由度の時と同じ感じ.テキトーにできる.
動吸振器

主系が調和外力を受けるときに,動吸振器を付加することにより,主系の振動応答を抑制することができる.
2.4 多自由度系の振動
減衰のない$${N}$$自由度の運動方程式も
$$
\bm{M}\ddot{\bm{x}}+\bm{Kx}=\bm{f}
$$
のカタチでまとめられる.
また,$${N}$$自由度系には,$${N}$$個の固有振動モードが存在する.
2.5 その他,基礎的な確認事項
知識問題関連
振動系の共振現象を回避するための対策として,「励振力の低減」,「励振力の卓越振動数と固有振動数の一致の回避」,「減衰比の増大」が有効である.
2自由度系以上の自由度を持つ振動系を多自由度振動系と呼ぶ.
動吸振器は機械や構造物などの制振対象物の振動を抑えるために,基礎と制振対象物の外に付加して用いられる.
軸変形を無視できる回転体(ロータ)を剛性ロータと呼び,静的および動的な釣り合い条件を満たすための修正不釣り合いは理論的には2つあれば良い.
振動系においてリミットサイクル現象や跳躍現象が見られる場合,対象となる系は多自由度非線形振動系でモデル化できる.(H31)
多くの場合,振動系の周囲の流体は系に減衰を与えるが,流体からの作用力が原因となって振動系が共振現象を起こす場合もある.
応答に複数の振動モードの影響が見られる場合,対象とする系を多モード振動系でモデル化する必要がある.
ラグランジアンは,系の運動エネルギーとポテンシャルエネルギーの差で定義される.
回転体の加速過程において危険速度を通過する必要がある場合には,できるだけ素早く回転数を上げて危険速度を通過させる必要がある.
系の分数調波共振やリミットサイクル挙動を説明するためには,非線形振動系モデルを用いる必要がある.(R1)
減衰の小さい連続体を固有振動数で加振した場合,振動振幅が局所的に小さくなる場所を反共振点と呼ぶ.
両端を支持され張力を受ける弦の振動モード形は複数存在する.
ダンパがクーロン摩擦でモデル化できる1自由度減衰振動系の自由振動の変位の包絡線は時間の一次関数となる.
系の周波数応答関数を実験的に得る一つの方法として,アクチュエータによるスイープ加振がある.(R3)
正弦加振力が作用する1自由度減衰振動系において,変位振幅倍率で表した周波数応答曲線の共振点となる振動数は,系の不減衰固有振動数よりも小さい.励振振動数が共振振動数より十分高くなると,変位振幅倍率の大きさは0に漸近する.
2質点集中質量系で表される2自由度非減衰振動系の固有モードのうち,固有振動数が低い方の固有モードは2つの質点の位相差が0となり,固有振動数が高い方の固有モードは2つの質点の位相差が$${\pi}$$となる.
非減衰振動系(主系)に減衰を持つ動吸振器を設置し,動吸振器の減衰が非常に小さい場合,動吸振器の固有振動数を励振振動数と等しくすると,主系の振動振幅は非常に小さくなるが,動吸振器の減衰を大きくすると,主系の振動振幅は大きくなる.
n自由度非減衰振動系の解を,固有モードの直交性を利用して,n個の1自由度系の解の重ね合わせで表すことができる.このような解析法をモード解析という.
両端を固定された一様な密度を持つ弦の固有振動数は,弦の張力が大きくなると大きくなり,弦の長さが長くなると小さくなる.(R4)
鉛直面内で運動する単振り子系において,重力は振り子に付加されたねじりばねとして作用する.
連続体で構成される物体をインパルス加振してその応答を周波数解析した場合,検出できる共振ピークの数は加振場所に依存する.
過減衰状態にある1自由度減衰振動系の初期変位応答は,粘性減衰係数を増加させると早く静的平衡点に近づく.
ハーモニカやクラリネットなどの楽器の音源となるリードの空気流による振動は,流体による平板の自励振動である.(R5)
運動方程式の立て方
マスバネダンパ系は簡単なので省略.
回転運動を含む系について,その運動方程式は,
$$
I \ddot\theta=N
$$
$${I}$$:慣性モーメント,$${N}$$:トルク(復元モーメントとか)
ねじり剛性(ねじりばね定数)を$${K}$$とすれば,復元モーメントは$${-K\theta}$$などと書ける.
復元力,復元モーメントなどの正負には十分注意する.対象物体の変位が十分に大きいときを考えて,正負を考えれば良い.
正負がキモい例(自分がバカなだけ):
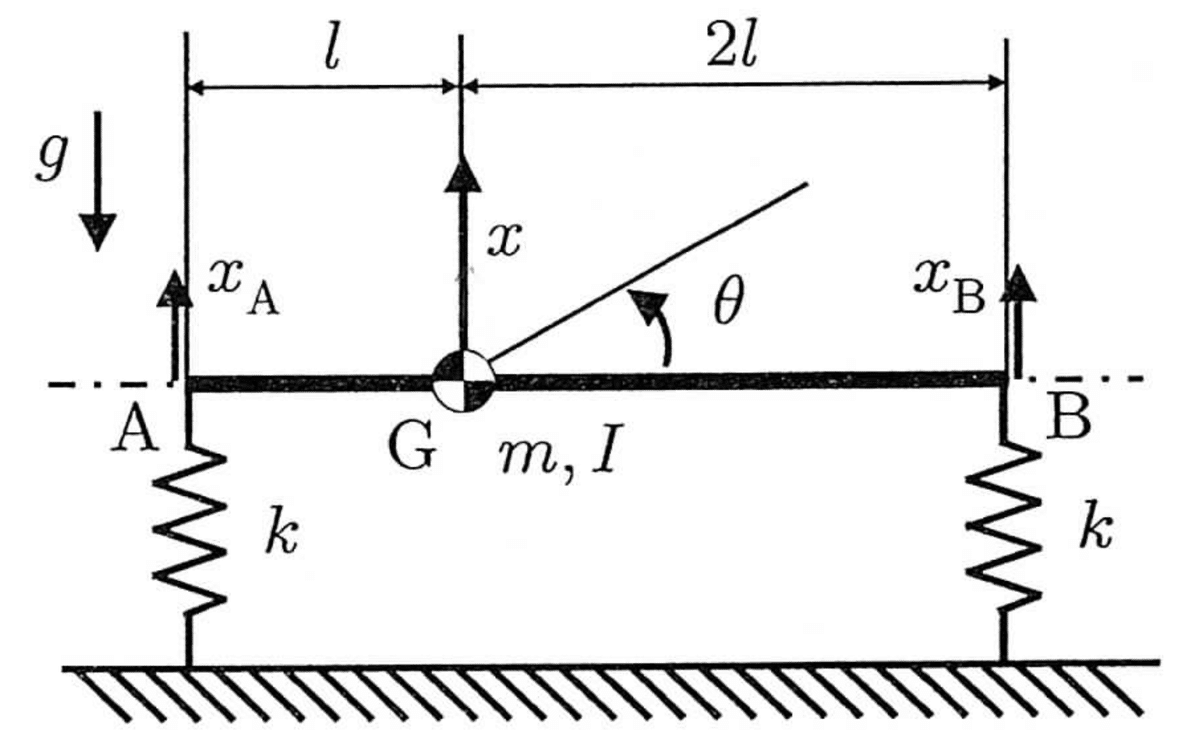
上下変位$${x}$$,回転変位$${\theta}$$についての運動方程式は,
$$
m\ddot x=-kx_A-kx_B \\
I\ddot\theta=-kx_B2l+kx_Al
$$
上下変位については納得.でも回転変位側は$${x_A}$$項が正なのがきもちわるい,復元モーメントはこの回転変位の向きなら負になっているはず.これは,$${x_A}$$自体にもうすでに負の情報が入っているから?見かけ上,正の項に見えるだけ?という解釈をしときます.
また,$${x_A,x_B}$$を$${x,\theta}$$を用いて表すと
$$
x_A=x-l\theta \\
x_B=x+2l\theta
$$
という幾何的な見方もしっかり抑える.
3. 熱力学
単語の穴埋めはJSMEテキストから.サイクルの構成図も頻出で,覚えた方がいいかも.
四力の中で最も時間を短縮することの出来る分野.問題文が短いものも多く,例題の解法を丸々暗記しちゃう.サイクル関連の知識をしっかりと身に付ける.
3.1 熱力学第一法則
熱力学第一法則は熱力学分野において重要なエネルギー保存の式であり,
$$
du = \delta q - \delta w
$$
で書ける.この式が意味するのは,内部エネルギーの微小変化は,系が受け取った微小熱量$${\delta q}$$から,系が外部に対してした微小仕事$${\delta w}$$を減じたものと等しい,ということである.もちろん,系が熱を失った場合は$${\delta q}$$が負,系が外部から仕事を受けた場合は$${-\delta w}$$が正となり,直感的な理解と一致するので正負には注意したい.
また,準静的過程においては$${\delta w = pdv}$$と書けるから,
$$
du = \delta q - pdv
$$
という式の方が見慣れているかもしれない.さらにこの式から定積変化($${dv=0}$$)の条件を加えれば,
$$
du = \delta q
$$
となるが,ここで定積比熱の定義を思い出せば,
$$
c_v = \left( \dfrac{∂q}{∂T} \right)_v
$$
であったからこの時,
$$
c_v = \left( \dfrac{∂u}{∂T} \right)_v
$$
が成立し,定積比熱は,単位温度あたりの定積条件下における内部エネルギーの変化に等しいことを意味する.また,理想気体においては,内部エネルギーは温度のみの関数であるから一般に,
$$
\varDelta u = c_v \varDelta T
$$
が成立する.問題解く時にめっちゃ使う!定積比熱は単位質量あたりの値であることに注意!
次にエンタルピー,および比エンタルピーを以下で定義する.
$$
H = U + PV
$$
$$
h =u + pv
$$
そして,比エンタルピーの微小変化量を考えると,
$$
dh=du+pdv+vdp
$$
今,定圧過程$${dp=0}$$を考えると,第一法則から,
$$
dh = \delta q
$$
となる.定圧比熱の定義は,
$$
c_p = \left( \dfrac{∂q}{∂T} \right)_p
$$
であるから,定圧過程において,
$$
c_p = \left( \dfrac{∂h}{∂T} \right)_p
$$
が成立.定圧比熱は,単位温度あたりの定圧条件下におけるエンタルピーの変化に等しいことを意味する.また,理想気体においては,
$$
\varDelta h = c_p \varDelta T
$$
が成立.こっちも大事!
基本的に問題には理想気体の条件があるから,上記二つの式を使ったら求値問題はなんやかんや解ける.
理想気体の状態方程式
$$
pv=RT
$$
まあ使う.
比熱比
$$
\kappa=\dfrac{c_p}{c_v}
$$
マイヤーの関係
$$
c_p-c_v=R
$$
等温過程
$$
\varDelta u=0 \\
q_{12}=w_{12}=\int_{1}^{2}pdv=RT\ln\dfrac{v_2}{v_1}=RT\ln\dfrac{p_1}{p_2}
$$
等圧過程
$$
w_{12}=p(v_2-v_1)=R(T_2-T_1) \\
q_{12}=\varDelta h =c_p(T_2-T_1) \\
\varDelta u = c_v(T_2-T_1)
$$
等積過程
$$
w_{12}=0 \\
q_{12}=\varDelta u=c_v(T_2-T_1)
$$
可逆断熱過程
$$
q_{12}=0 \Rightarrow \varDelta s =0\\
pv^{\kappa}=const. \\
Tv^{\kappa-1}=const. \\
\dfrac{T}{p^{\frac{\kappa-1}{\kappa}}}=const.
$$
ポリトロープ過程
$$
pv^n=const. \\
n=0 \Rightarrow 等圧過程 \\
n=1 \Rightarrow 等温過程 \\
n=\kappa \Rightarrow 可逆断熱過程 \\
n=\infin \Rightarrow 等積過程
$$
結局,問題を実際に解くときによく使うのは以下
$$
du=\delta q-\delta w \\
pv=RT \\
du=c_vdT \\
dh=c_pdT
$$
3.2 熱力学第二法則
・理論最大熱効率
$$
\eta_{carnot}=1 - \dfrac{T_L}{T_H}
$$
・エントロピーの定義
$$
ds=\dfrac{\delta Q_{rev}}{T}
$$
添え字のrevはreversible(可逆)を示し,一般的な不可逆過程と区別をする.
・可逆過程でのエントロピー変化量
$$
\varDelta s = \int_{1}^{2}\dfrac{\delta Q_{rev}}{T}
$$
・不可逆過程におけるエントロピー生成
$$
ds_{gen}=ds-\dfrac{\delta Q}{T}
$$
あらゆる不可逆過程において$${s_{gen}>0}$$であり,可逆過程においてのみ$${s_{gen}=0}$$となり,エントロピーは一定であり保存される.$${s_{gen}<0}$$は起こり得ない.
エントロピーの利用
エントロピー変化の式:$${Tds}$$の関係式
$$
Tds=du+pdv \\
Tds=dh-vdp
$$
理想気体のエントロピー変化
$${pv=RT}$$,$${du=c_vdT}$$,$${dh=c_pdT}$$より,
$$
\begin{align*}
\varDelta s &= c_v\int_{1}^{2}\dfrac{dT}{T} + R\int_{1}^{2}\dfrac{dv}{v} \\
&= c_p\int_{1}^{2}\dfrac{dT}{T} - R\int_{1}^{2}\dfrac{dp}{p}
\end{align*}
$$
液体,固体のエントロピー変化
気体に比べて体積変化が小さく,$${dv=0}$$とでき,
$$
\begin{align*}
\varDelta s &= c\int_{1}^{2}\dfrac{dT}{T} \\
&= c\ln(\dfrac{T_2}{T_1})
\end{align*}
$$
つまり,固体や液体の場合は比熱が分かれば,最初の温度と最後の温度が決まると,エントロピー変化の計算ができる.
エントロピー生成の計算
系内に不可逆過程がない(内部可逆)場合,$${s_{gen}=0}$$.不可逆過程を含む孤立系では,エントロピー輸送の項はゼロとなり,エントロピー生成は全て系内のエントロピー変化になり,$${s_{gen}=\varDelta s}$$.
まあ,実際の問題ではエントロピー変化をとりあえず求めればおk!
例題:H31問2(3)(4)
(3)$${\varDelta s=\dfrac{2256\times0.5}{100+273}=\dfrac{1128}{373}\approx3.02}$$[kJ/K]
(4)$${Z=\dfrac{-3000}{80+273}+\dfrac{3000}{60+273}\approx0.51}$$[J/K]
3.3 ガスサイクル
・理論熱効率
$$
\eta_{th}=\dfrac{L}{Q_H}=1 - \dfrac{Q_L}{Q_H}
$$
ピストンエンジンのサイクル
・オットーサイクル(火花点火エンジン)
一般に可燃性混合気を吸入・圧縮して激しく乱れた流れ(高乱流)のもとで点火し,極めて急速な火炎伝播により燃焼する.
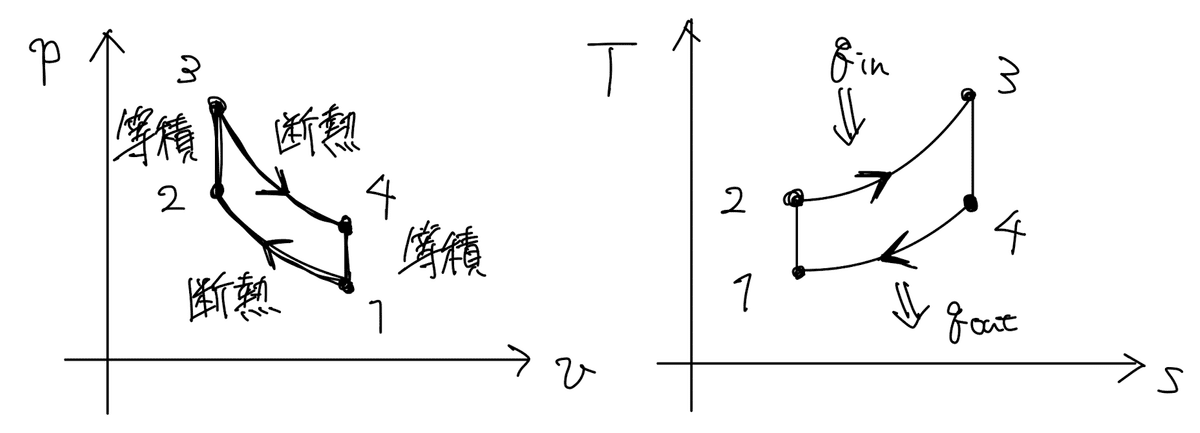
作動ガスは1の状態から断熱的に圧縮され,高温高圧の状態2となる.ここで,体積一定のまま燃焼により加熱されて状態3となったのち,断熱的に膨張し4の状態となり,さらに体積一定のまま冷却され状態1に戻ってサイクルを完了する.熱効率は$${\eta_{Otto}=1-(\dfrac{v_2}{v_1})^{\kappa-1}}$$となる.
・ディーゼルサイクル

ディーゼルエンジンでは空気のみをシリンダ内で圧縮して高温高圧とし,そこに燃料を霧状に高圧噴射する.燃焼室内は激しく乱れた流れ,すなわち高乱流場となっており,燃料と空気が迅速に混合して可燃混合気が形成されるとともに,自着火条件を満たした部分から順に燃焼が進行する.熱効率は$${\eta_{Diesel}=1-\dfrac{T_4-T_1}{\kappa(T_3-T_2)}}$$である.
・サバテサイクル(出なさそう)
オットー+ディーゼルみたいな.

$${\eta_{Sabathe}=1-\dfrac{c_v(T_4-T_1)}{c_v(T_{2'}-T_2)+c_p(T_3-T_2)}}$$
・スターリングサイクル
外燃式のピストンエンジンに適応されるガスサイクル.実用化・高性能化を目指して研究開発途中? このサイクルの実現には高性能の加熱器および熱交換器が必要.

熱効率は$${\eta_{Stirling}=1 - \dfrac{T_1}{T_2}}$$で,二つの高低温度間で作動するカルノーサイクルの熱効率と一致.
ガスタービンエンジンのサイクル

・ブレイトンサイクル
ガスタービンの基本サイクルでは受熱と放熱が等圧過程で行われる.ジェットエンジンもこれ.

熱効率は$${\eta_{Brayton}=1 - \dfrac{T_4-T_1}{T_3-T_2}}$$
→ブレイトン再生サイクル(出なさそう)
・エリクソンサイクル
ブレイトンサイクルに中間冷却再熱を施したもの(?).
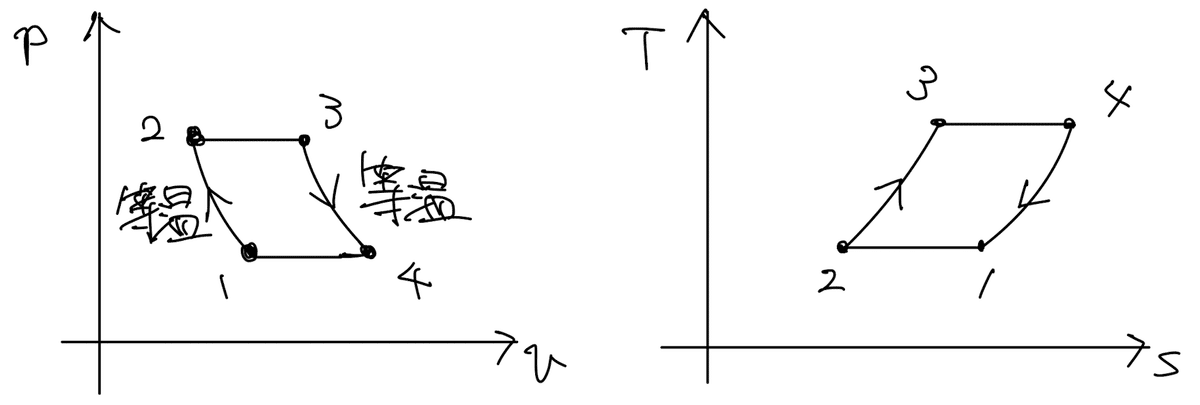
熱効率は$${\eta_{Ericsson}=1 - \dfrac{T_1}{T_3}}$$で,カルノーサイクルの熱効率と一致.
T-s線図において,等圧過程の場合はエントロピーを上昇させるのにある程度の温度上昇が必要.一方,等積過程の場合は,少しの温度上昇でエントロピーが上昇する.
3.4 蒸気サイクル
湿り蒸気1kgに乾き飽和蒸気が$${x}$$(kg),飽和液が$${1-x}$$(kg)含まれているとき,その湿り蒸気の乾き度は$${x}$$であるという.
蒸発熱$${r}$$は$${r=h''-h'}$$で表される.
・湿り蒸気の性質(':飽和液,’’:飽和蒸気)
$$
h=h' + (h''-h')x \\ u=u'+(u''-u')x \\ s=s' + (s''-s')x \\ s''-s' = \dfrac{r}{T}
$$
・ランキンサイクル
ランキンサイクルは基本蒸気サイクルであり,以下図に示すように,ボイラ,タービン,復水器,給水ポンプより構成される.ほとんどのシステムの作動物質は水である.
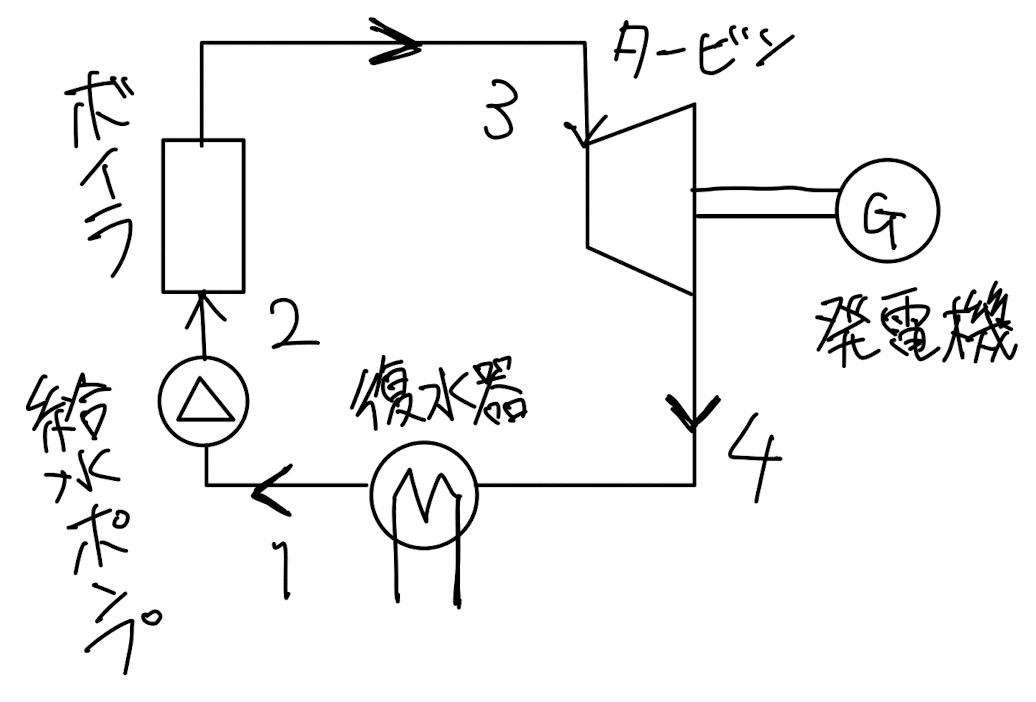
低圧の液はポンプで可逆断熱圧縮されて高圧の圧縮液になり(状態1→2),ボイラで等圧加熱されて高温高圧の蒸気になる(状態2→3).その後,タービンで可逆断熱膨張して機械仕事を行なって低圧の湿り蒸気になり(状態3→4),復水器で等圧冷却されて低圧の飽和液に戻る(状態4→1).4つの変化の過程はガスサイクルのブレイトンサイクルと同じであるが,気液の相変化を伴うため,T-s線図はかなり異なっている.
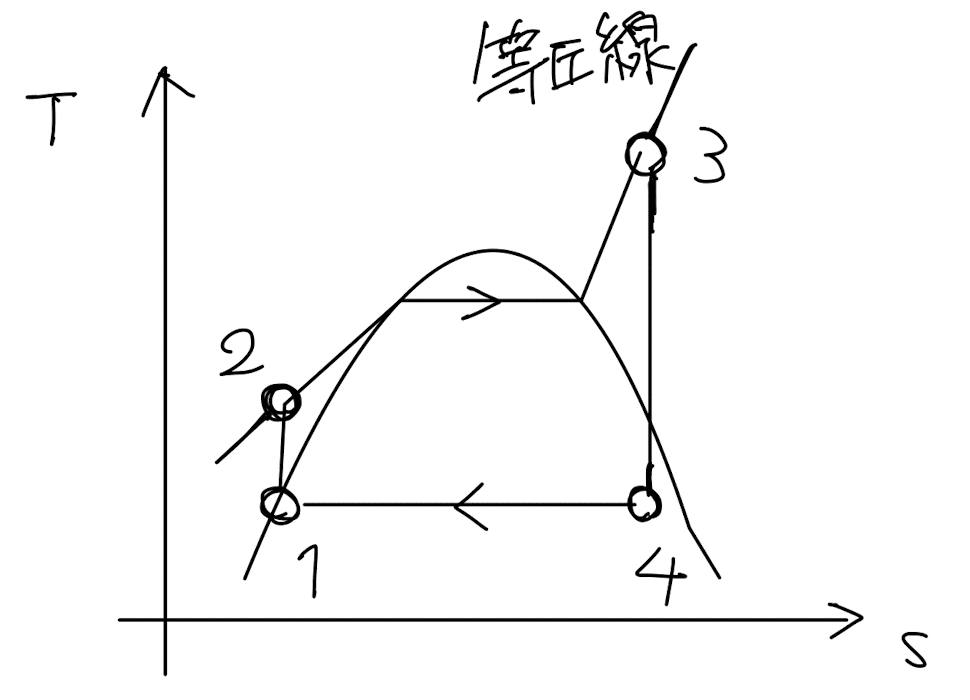
例題:R1(2020)問1
火力発電に用いられる蒸気原動機サイクルは,主にボイラ,タービン,復水器,ポンプより構成されており,水蒸気が有する高温高圧のエネルギーを機械仕事に変換する熱機関である.低圧の液水はポンプで断熱圧縮されて圧縮液になり,ボイラで等圧的に加熱される.飽和液の状態から蒸発が始まり,温度一定で気体と液体が共存した湿り蒸気を経て,水の蒸発が完了した瞬間に乾き飽和蒸気になる.さらに加熱され過熱蒸気になった後タービンに入る.タービンの中で蒸気が膨張し出口では湿り蒸気になる.タービン入口での水蒸気温度を上げるほど熱効率は高くなるが,材料の耐熱性の問題から,現状のタービン入口温度は900K程度が限界である.また,タービン出口での乾き度は88~90%の範囲に収まるように設計される.
例題:R5(2024)問5
(1)$${s_4=s_3}$$であるから$${s_4=6.57}$$[kJ/kg•K]
(2)$${s_4=s'+(s''-s')x}$$であるから,$${x=\dfrac{s_4-s'}{s''-s'}=\dfrac{6.57-0.649}{8.15-0.649}\approx0.789}$$
(3)$${h_4=h'+(h''-h')x\approx192+(2580-192)\times0.789\approx2.08\times10^3}$$[kJ/kg•K]
(4)求める値は$${h_3-h_2}$$である.今,ポンプ動力が無視できるから$${h_2= h_1}$$.$${h_1}$$は飽和液の比エンタルピーであるから(∵復水器では等圧冷却されて低圧の飽和液に戻る),$${h_1=h'}$$.したがって,$${h_3-h_2= h_3-h'=3150-192\approx2.96\times10^3}$$[kJ/kg]
(5)$${h_3-h_4\approx3150-2076\approx1.07\times10^3}$$[kJ/kg]
(6)$${\eta=\dfrac{w}{q_{in}}=\dfrac{h_3-h_4}{h_3-h_2}\approx\dfrac{1.07\times10^3}{2.96\times10^3}\approx0.361}$$
3.5 冷凍サイクル
冷凍機とヒートポンプ
成績係数は以下で定義される
$$
\varepsilon_R=\dfrac{Q_L}{L} =\dfrac{Q_L}{Q_H-Q_L}
$$
$$
\varepsilon_H=\dfrac{Q_H}{L} =\dfrac{Q_H}{Q_H-Q_L}
$$
$${L}$$:仕事入力,$${Q_L}$$:低温熱源からの受熱量,$${Q_H}$$:高温熱源への放熱量
可逆の冷凍機やヒートポンプ(最高効率のもの,逆カルノーサイクル)の場合
$$
\varepsilon_{R,carnot}=\dfrac{T_L}{T_H-T_L}
$$
$$
\varepsilon_{H,carnot}=\dfrac{T_H}{T_H-T_L}
$$
電熱ヒーター:成績係数=1
4. 流体力学
粘性流体,境界層,抗力・揚力,複素ポテンシャルなどを中心に下記の参考書で勉強.誘導が丁寧だからどうにかなるよいっ
4.1 基礎方程式
質量保存則,運動量保存則
$$
\dfrac{\partial\rho}{\partial t}+\dfrac{\partial\rho v_i}{\partial x_i}=0
$$
$$
\dfrac{\partial\rho v_i}{\partial t}+\dfrac{\partial\rho v_i v_j}{\partial x_j}+\dfrac{\partial p}{\partial x_i}=\dfrac{\partial\sigma_{ij}}{\partial x_j}+\rho F_i
$$
・非圧縮流れ
$$
\dfrac{D\rho}{D t}=\dfrac{\partial\rho}{\partial t}+v_j\dfrac{\partial\rho}{\partial x_j}=0
$$
粘性流体,非圧縮流れの場合
$$
\dfrac{\partial v_i}{\partial x_i}=0
$$
$$
\rho\dfrac{D v_i}{D t}+\dfrac{\partial p}{\partial x_i}=\mu\dfrac{\partial^2v_i}{\partial x_j^2}+\rho F_i
$$
理想流体,非圧縮流れの場合
$$
\dfrac{\partial v_i}{\partial x_i}=0
$$
$$
\rho\dfrac{D v_i}{D t}+\dfrac{\partial p}{\partial x_i}=\rho F_i
$$
定常の理想流体におけるベルヌーイの定理
$$
\dfrac{\bm u^2}{2}+\dfrac{p}{\rho}+gz=const
$$
様々な問題でよく使うので,しっかりと覚えて実際に使えるようにする.
連続の式
$$
A_0v_0=A_1v_1
$$
こちらもよく使う.ここで,$${A}$$は断面積であり,$${v}$$は断面を通過する流体の速度である.
運動量法則
『流体が受ける力=運動量変化量』
$${m \Delta v= F \Delta t}$$を両辺$${\Delta t}$$で除して,単位時間あたりで考えているもの.力が聞かれる系統の問題はだいたいこの式使えばおk.
4.2 渦・速度ポテンシャル・流れ関数
渦度ベクトル$${\bm\omega}$$は以下で定義される.
$$
\bm\omega=\nabla\times\bm v=\begin{pmatrix} \dfrac{\partial v_z}{\partial y}-\dfrac{\partial v_y}{\partial z}\\ \dfrac{\partial v_x}{\partial z}-\dfrac{\partial v_z}{\partial x} \\ \dfrac{\partial v_y}{\partial x}-\dfrac{\partial v_x}{\partial y}\end{pmatrix}
$$
渦度ベクトルの大きさが大きいほど,クルクル回ります.()
渦なし流れ(渦度ベクトルが0)
$$
\dfrac{\partial v_i}{\partial x_j}=\dfrac{\partial v_j}{\partial x_i}
$$
循環
$$
\begin{align*}
\Gamma&=\oint_C \bm{v} \cdot d\bm{s} \\
&=\oint_C (udx+vdy) \\
&=\iint_S \bm{\omega}dxdy
\end{align*}
$$
すなわち,循環とは渦度(ベクトル)の面積分.ストークスの定理については↓ベクトル解析で復習.
ケルビンの循環定理
外力が保存力で,密度が一定である理想流体では,流れとともに移動する閉曲線$${C}$$に沿う循環は時間的に不変.
速度ポテンシャル
あるスカラー関数$${\phi(x,y,z,t)}$$を用いて速度$${\bm{u}=(u,v,w)^\mathsf{T}}$$を以下で書くとき,
$$
\bm{u}=\begin{pmatrix} u \\ v \\ w\end{pmatrix}=\begin{pmatrix} \frac{\partial \phi}{\partial x}\\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z}\end{pmatrix}
$$
スカラー関数$${\phi}$$を速度ポテンシャルと呼び,流れは渦なしとなり,渦なし流れをポテンシャル流れという.
速度ポテンシャルの例
一様流
$$
\phi=ax+by+cz
$$
壁に当たる流れ
$$
\phi=\dfrac{a}{2}(x^2-y^2)
$$
湧き出し,吸い込み
$$
\phi(r)=-\dfrac{m}{r},r=\sqrt{x^2+y^2+z^2}
$$
$${m>0}$$で湧き出し.$${m<0}$$で吸い込み.
流れ関数
二次元,非圧縮流体の流れ場において,
$$
u=\dfrac{\partial \psi}{\partial y},v=-\dfrac{\partial \psi}{\partial x}
$$
を満たすスカラー関数$${\psi}$$:流れ関数が必ず存在.渦ありでも渦なしでもおk.
複素ポテンシャル
二次元非圧縮流体+渦なしを考えると,
$$
u=\dfrac{\partial \phi}{\partial x}=\dfrac{\partial \psi}{\partial y} \\
v=\dfrac{\partial \phi}{\partial y}=-\dfrac{\partial \psi}{\partial x}
$$
ここで,$${z=x+iy}$$を用いて,複素ポテンシャル$${W(z)}$$を
$$
W(z)=\phi(z)+i\psi(z)
$$
で定義する.$${u,v}$$に関する上式は,$${W(z)}$$が正則であるためのコーシー•リーマンの関係式そのものである.つまり,数学的には$${W(z)}$$の正則性を表すCR関係式は,流体力学的には,速度ポテンシャル$${\phi}$$と流れ関数$${\psi}$$が定義できる条件を示したものとなる.
複素速度
$$
\dfrac{dW}{dz}=u-iv
$$
速度ベクトルの複素数表示を$${\bm{u}=u+iv}$$とすると,
$$
\dfrac{dW}{dz}=u-iv=\overline{\bm{u}} \\
$$
$$
\therefore |\bm{u}|^2=u^2+v^2=\left( \dfrac{dW}{dz}\right)\overline{\left(\dfrac{dW}{dz}\right)}
$$
複素ポテンシャルの例
一様流
$$
W(z)=U_0z
$$
$${U_0}$$:実定数
角をまわる流れ
$$
W(z)=Az^n
$$
角度$${\dfrac{\pi}{n}}$$で交わる2平面の流れを表す.特に,$${n=2}$$で直角をまわる流れを表す.
湧き出しと吸い込み
$$
W(z)=m\ln z
$$
$${m>0}$$:湧き出し,$${m<0}$$:吸い込み
渦糸
$$
W(z)=-ik\ln z=\dfrac{\Gamma}{2\pi i}\ln z
$$
$${\kappa=\dfrac{\Gamma}{2\pi}}$$:実定数,$${\Gamma}$$:渦糸の強さ,循環
$${z=re^{i\theta}}$$を代入して,速度ポテンシャルから$${r,\theta}$$方向速度を求めると,
$$
v_r=\dfrac{\partial \phi}{\partial r}=0 \, ,
v_\theta=\dfrac{1}{r}\dfrac{\partial \phi}{\partial\theta}=\dfrac{\Gamma}{2\pi r}
$$
となり,速度は$${\theta}$$方向成分のみ.$${\propto\dfrac{1}{r}}$$.
円柱周りの流れ(大体これ)
速度$${U}$$の一様な流れに置かれた半径$${a}$$の円柱周りの流れは以下で表される.
$$
W(z)=Uz+\dfrac{Ua^2}{z}
$$
循環を伴う円柱周りの流れ
一様流の円柱周りの流れに時計回りの循環$${-\Gamma}$$を与えると,
抗力$${D=0}$$ 循環の有無に依らず,流れの中にある円柱には抵抗が働かない($${\because}$$粘性を無視しているから)
揚力$${L=\rho U \Gamma}$$ 流れの中にある円柱に循環$${-\Gamma}$$が与えられると,揚力が発生(クッタ•ジューコフスキーの定理)
流れの中に回転する物体があるとき,流れに垂直方向の力が働く.(マグナス効果)
等角写像
等ポテンシャル線($${\phi=const}$$)と流線($${\psi=const}$$)は直交する.
一般に,複素関数$${\zeta(z)}$$が正則であれば,$${z}$$平面上の任意の2本の曲線の交わる角度は$${\zeta}$$平面上への写像によっても変わらない.このことを等角写像という.
等角写像は流れの変換に応用でき,よく性質が調べられている円柱周りの流れを媒介として,直接求めるのが難しい平板や翼周りの流れの複素ポテンシャルを求めることが出来る!
ジューコフスキー変換
$$
\zeta=z+\dfrac{a^2}{z}
$$
$${z}$$平面で半径$${a}$$の円は写像$${\zeta}$$により,長さ$${4a}$$の平板に変換される.
$${z}$$平面で第2象限中心の円は写像$${\zeta}$$により,ジューコフスキー翼に変換される.
迎え角のある流れ
$$
z'=ze^{-i\alpha}
$$
とすることで$${\alpha}$$だけ回転.長さ$${4a}$$の平板について,そのよどみ点は$${2a\cos \alpha,-2a\cos \alpha}$$となる.
クッタの条件
翼の後端を岐点とすること.辻褄合わせの循環が以下で定まる(長さ$${4a}$$の平板の場合?).
$$
\Gamma=4 \pi aU\sin\alpha
$$
4.3 境界層
非圧縮性流体における二次元の境界層方程式
$$
\dfrac{\partial u}{\partial t}+u\dfrac{\partial u}{\partial x}+v\dfrac{\partial u}{\partial y}=-\dfrac{1}{\rho}\dfrac{\partial p}{\partial x}+\nu\dfrac{\partial^2 u}{\partial y^2} \\
-\dfrac{1}{\rho}\dfrac{\partial p}{\partial y}=\mathcal{O}(\delta)
$$
定常なら,
$$
u\dfrac{\partial u}{\partial x}+v\dfrac{\partial u}{\partial y}=U_e\dfrac{dU_e}{dx}+\nu\dfrac{\partial^2 u}{\partial y^2}
$$
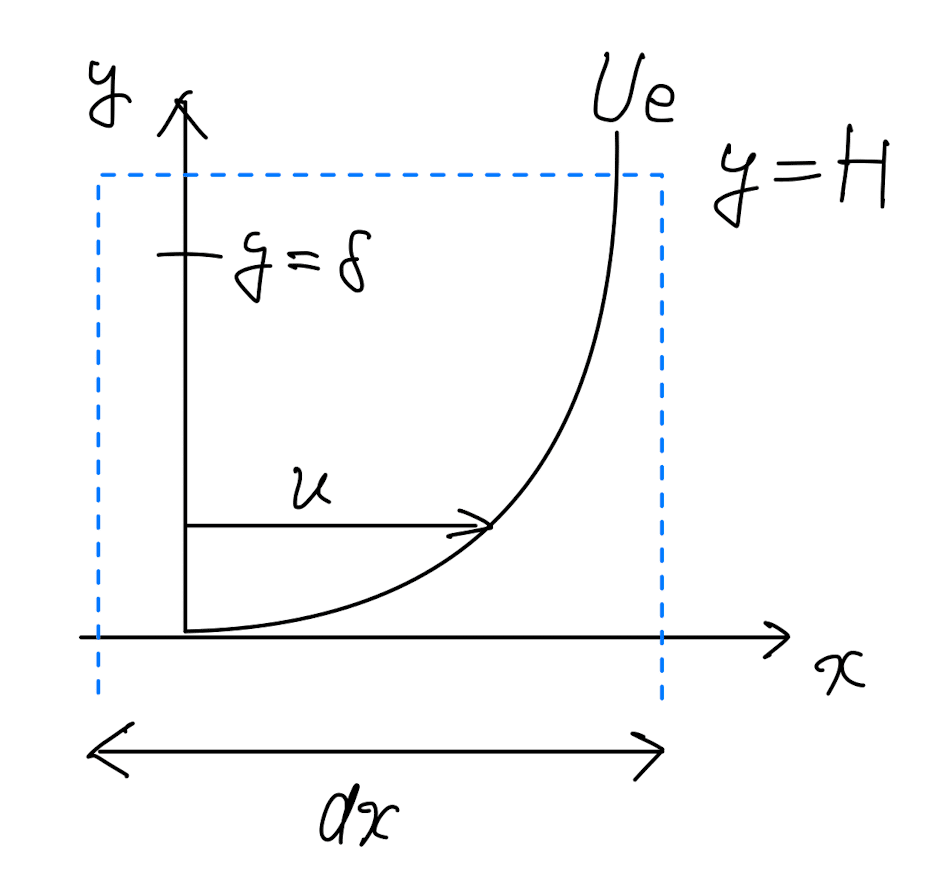
上図のような二次元流れを考える.検査体積内に左から流入する質量は,
$$
\int_{0}^{H}\rho udy
$$
である.一方,右側から流出する質量は,
$$
\int_{0}^{H}\rho udy+\dfrac{d}{dx}(\int_{0}^{H}\rho udy)dx
$$
となる.流れが定常で,検査体積内の質量は保存されるので,上2式の差は,検査体積の上部から流入しなければならない.検査体積内に左側から流入する運動量は,
$$
\int_{0}^{H}\rho u^2dy
$$
となる.一方,右側から流出する運動量は,
$$
\int_{0}^{H}\rho u^2dy+\dfrac{d}{dx}(\int_{0}^{H}\rho u^2dy)dx
$$
である.検査体積の上部から流入する質量によって検査体積内に輸送される$${x}$$方向の運動量は,
$$
U_e(x)\dfrac{d}{dx}(\int_{0}^{H}\rho udy)dx
$$
である.したがって,検査体積に流入する運動量と,流出する運動量の差は,
$$
\dfrac{d}{dx}(\int_{0}^{H}\rho u^2dy)dx-U_e(x)\dfrac{d}{dx}(\int_{0}^{H}\rho udy)dx
$$
で与えられる.ここで,運動量の法則から,$${x}$$方向の運動量の変化は流体に作用する$${x}$$方向の力の総和とつり合う.よって,圧力と剪断応力とか色々考えると,結局,
$$
-\tau_w-H\dfrac{dp}{dx}=-\rho\dfrac{d}{dx}\left(\int_{0}^{H}(U_e(x)-u)udy\right)+\dfrac{dU_e(x)}{dx}\rho\left(\int_{0}^{H} udy\right)
$$
を得る.これらの式をカルマンの積分条件といい,境界層に対する運動量方程式である.
排除厚さ
$$
\delta^*=\int_{0}^{\delta}\left( 1-\dfrac{u}{U_e}\right)dy
$$
運動量厚さ
$$
\theta=\int_{0}^{\delta}\left( 1-\dfrac{u}{U_e}\right)\dfrac{u}{U_e}dy
$$
4.4 抗力と揚力
抗力係数と揚力係数
$$
C_D=\dfrac{D}{\dfrac{1}{2}\rho U_\infin^2S}
$$
$$
C_L=\dfrac{L}{\dfrac{1}{2}\rho U_\infin^2S}
$$
$${U_\infin}$$:一様流速度,$${\rho}$$:流体の密度,$${S}$$:流れに直角な面への物体の投影面積
平板:摩擦抵抗:大
円柱:圧力抵抗:大
レイノルズ数が一定値(2.00×10^5)を超えると,抗力係数は急激に低下し,約0.2となる.これは境界層が乱流遷移し,剥離点が後方に移動するためである.
4.5 粘性流体関連
レイノルズの相似則
$$
Re = \dfrac{\rho UL}{\mu} = \dfrac{UL}{\nu}
$$
レイノルズ数:低 → 粘性の影響:大
レイノルズ数:高 → 粘性の影響:小
レイノルズ数が等しければ流れは相似.模型などでシミュレーション可能
粘性流体の剪断応力(ニュートンの粘性の法則)
$$
\tau = \mu \dfrac{\partial u}{\partial y} = \rho \nu \dfrac{\partial u}{\partial y}
$$
円菅内の粘性流れ
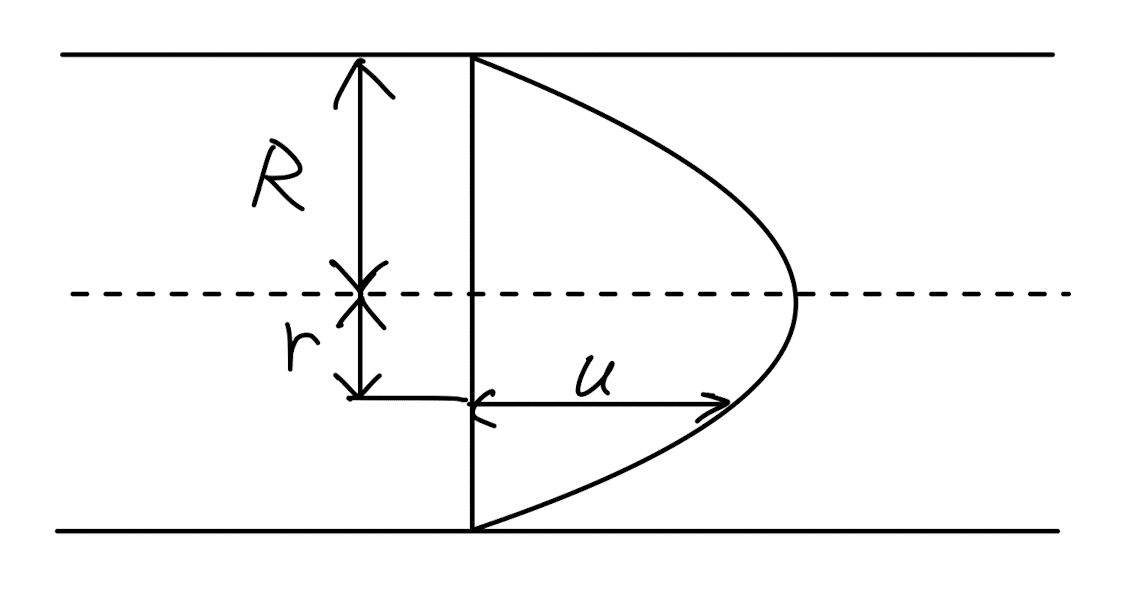
なんやかんやあって,速度分布は,
$$
u=-\dfrac{1}{4\mu}(R^2-r^2)\dfrac{dp}{dx}
$$
ハーゲン・ポアズイユ流れという.
平行平板間の流れ

ナビエ・ストークス方程式は,色々あって,
$$
\dfrac{dp}{dx}=\mu\dfrac{d^2u}{dy^2}
$$
境界条件から,速度分布は,
$$
u=U_1+\dfrac{U_2-U_1}{h}y-\dfrac{h^2}{2\mu}\dfrac{dp}{dx}\{(\dfrac{y}{h})-(\dfrac{y}{h})^2\}
$$
流量$${Q}$$は,
$$
Q=\int_{0}^{h}udy=U_1h+(U_2-U_1)\dfrac{h}{2}-\dfrac{h^3}{12\mu}\dfrac{dp}{dx}
$$
平板の一方が固定され,他方が$${x}$$方向に運動する場合の流れを,一般にクエット流れという.
最終確認
1.試験時間は短い.
2.知識問題は考えても意味がない.
3.捨て問を設けても良いが獲れるところは絶対に落とさない.
この記事が気に入ったらサポートをしてみませんか?
