
熱力学・統計力学 第18章問題解説
「熱力学・統計力学 熱をめぐる諸相」第18章章末問題の解説。解答例はこちらを参照。
18章は応用編の導入という位置づけである。いくつか、相互作用のある系の扱い方を議論した。物理現象を本格的に記述するというにはほど遠いが、どういう問題や扱い方がありえるか、とっかかりになる議論を扱った。前半と後半で内容が違うので戸惑うかもしれない。講義ノートの時点では章を分けていたが、出版時にいろいろ考えて一つにまとめた。いろいろな方向性やアプローチがあるのだと捉えていただきたい。その代わりといってはなんだが、18.1節を入れて背後にある問題意識を強調した。
[18-1] 二原子分子
本文で行った問題と同じだが、座標・運動量の全てを極座標で扱う。意図することは二つある。
座標変換を行うとヤコビアンを計算しなければならないが、共役運動量も含めて変換するとヤコビアンは1となる(Liouvilleの定理)。座標を変換した場合にあらわれる$${r^2\sin\theta}$$は、運動量の積分から自然に出てくる。解析力学の復習になるが、問16.1(248ページ)で示したことの確認である。
本文で熱容量のふるまいを等分配則から解釈した。重心運動量3+相対運動量3+相対座標1である。ここでは相対運動の部分4を回転2+振動2と解釈する。極座標を用いて積分を表すことによってそれが可能となる。
(a). 与えられた座標系に対して共役運動量がどのようになるかは自明ではない。次元解析などからある程度のものは予想できるが、正しい形を得るためには、定義通りラグランジアンから考える必要がある。ややめんどうであるが、他の汎用的な方法もないし(何かあるのだろうか?)、そうするしかないと思われる。
[18-2] 不完全気体
理想気体からのずれを扱う。ここで扱う方法は、わずかなずれを二つのパラメータを用いて捉えようというものである。どんな系にも適用できるわけではないし、大きくずれたときまで記述できるわけではない。ただ、本文で扱ったように、ミクロな描像(短距離での強い斥力と長距離での弱い引力という相互作用の性質)から期待される効果が熱力学関数にどのように反映されるかを議論できる。
(a). 近似の範囲でvan der Waals方程式(2-3.1)式(36ページ)と一致する。そのことと、18.3節の議論を用いると、$${b}$$は粒子間の強い斥力によって実効体積が小さくなる効果($${V\to V-Nb}$$)、$${a}$$は弱い引力によって圧力が小さくなる効果($${P=\frac{Nk_BT}{V}\to \frac{Nk_BT}{V}-\frac{N^2}{V^2}a}$$)を表しているとわかる。
(c). 内部エネルギーが体積に依存するので、断熱自由膨張で温度が変化するようになる。何かのずれを議論するときは、ずれを取り入れることによってはじめて生じる現象を扱うのが賢い。問題[7-12]のJoule-Thomson効果でもそのようなことを議論した。(d)も同様である。
[18-3] 1次元の相互作用する系
相互作用する系の分配関数を計算することはほとんどの場合困難であるが、特殊な場合には積分を実行することができる。その一例として、1次元の相互作用する系を扱う。
積分を実行できるのは、粒子が一列に揃っていて、さらに、互いの順番が変わらないからである。次章で扱うIsing模型に似ている。特殊な状況であるが、相互作用の効果をまともに扱える模型はほとんど存在しないため、貴重な例となる。
もう一つ、アンサンブルを変更するという方法を用いている。18章本文最後で言及したように、一般に、示強量を変数とした方が計算がしやすくなる。ゴム弾性とこの問題でそのことが実感できるはずである。まだできなくても、具体例はこれから何度も出てくる。特に、第IV部ではそのことが議論の中心の一つとなる。
(a). 各変数の積分範囲に注意。(A18-3.3a)式では階段関数を用いて積分の上限を無限大にしている。その他の要素も含めて、解答例にあるひとつひとつの変形をよく確認して意味を理解してほしい。
(c). パラメータが複数あるのでややこしい。どのようにプロットするかよく考える必要がある。まずはプロットするときの鉄則として、無次元化を考える(付録A.4参照)。解答例では(A18-3.7)式を(A18-3.11)式のように書いて考えている。
普通は両極限での漸近形がわかれば全体の概形を得ることは難しくない。この場合は両極限でのふるまいがよく似ているので、どうプロットするか戸惑うかもしれない。図を見ると、ふたつの関数の間をうまくつないでいることがわかる。

(d). 18.3節で考えた要素(強い斥力と弱い引力)をもっているため、一般論で考えた性質が導かれることがわかる。厳密に解ける具体的な模型による裏付けとなる。ただ、高次元などに一般化したときに同様のふるまいが得られるかどうかは定かではない。高次元では他のさまざまな要素が生じうると考えられるため、得られる性質はそんなに単純ではないだろう。そもそも今の1次元の場合でも、相互作用の形を単純で扱いやすいものに設定している。
[18-4] 1次元の相互作用する系:変分法
前問の系を変分法を用いて解いてみる問題。計算はかなりややこしい。摂動や変分法はこういうややこしい計算になることが多い。
普通に解けるものをわざわざ近似計算させて、しかもそっちの方がめんどうという、やや意地悪な問題であるが、近似がどの程度厳密解に近いものを出すかをはかる意味ではよい練習問題になる。計算練習にもなる。計算はたくさん手を動かして慣れないと身につかない。
どんな感じで計算しているか、ノートを貼っておく。


この程度の近似の場合、得られる結果は比較的簡単に理解できる。この問題で言うと、相互作用の性質によって有効振動数$${\Omega}$$が$${\omega}$$より大きくなるか小さくなるかが決まる。
近似的に解くことが理解を促進させることもある。厳密解を得ても何をどう見たらよいかは決して自明ではない。この問題では、有効振動数という概念を用いて答えを捉えている。そうすると解がイメージしやすくなる。もっとも、この問題で調和振動子という概念にあてはめて解を解釈するのが妥当であるかはわからない。解けない問題を調べるときは、いろいろ試行錯誤して系の性質を探る。
[18-5] 断熱冷却
ちょっとした応用。現実の冷却器でも用いられている原理である。
ただし、同じ操作を理想気体などの系で行うと、温度は上がる。そのような違いがでるのは、$${\left(\frac{\partial S}{\partial V}\right)_T}$$(ゴム弾性の場合、体積$${V}$$は長さ$${L}$$と解釈する)の符号が異なるからである。その場合、冷却させるには、逆の操作をすればよい。つまり、まず圧縮させて放置し、膨張させる。
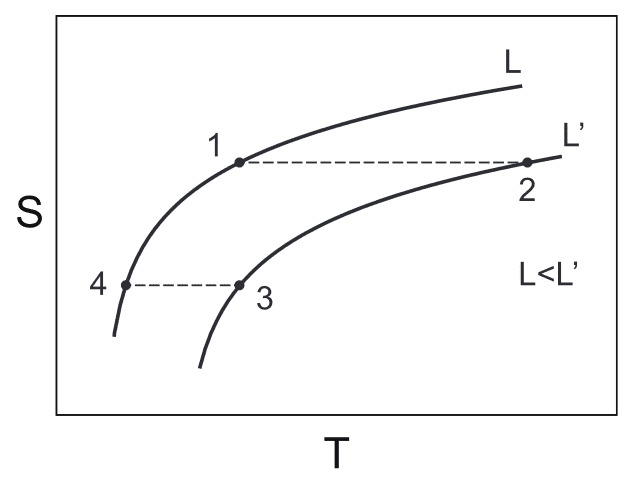
このことも問題にすればよかったと今になって思う。
[18-6] 弾性体の統計力学模型:回転の効果
基本的には本文の計算と同じである。違いは変数の取り方が異なることである。結果もよく似ている。本文で扱ったとびとびの値より本問で扱った連続的な方が現実的という気もするが、ふるまいが大きく変わるわけではない。それは結局のところ本文で少し言及したように、他の要素を全て無視したミニマル模型となっているからである。もう少し現実的にしようとすると計算は簡単には実行できなくなる。
近年の発展で言えば、ゴム弾性というかゲル弾性であるが、溶媒との相互作用の効果を取り入れたこの研究が個人的には面白かった。統計力学的模型を構成するのだが、それほど複雑なものではない。もちろん、解くのは簡単ではなく、特殊な場合を除いて数値計算を用いているが、実験に近いふるまいを再現できるなど、興味深い。
変数をとびとびか連続的にすることは次章のスピン模型でも見られる。章末問題[19-1]を参照。
[18-7] 弾性体の統計力学模型:張力の効果
本文で扱った例ではエントロピー弾性に着目していたため、エネルギーの寄与は一切無視されていた。したがってハミルトニアンというものが一切出てこなかった。本問ではハミルトニアンが出てくるが、外部ポテンシャルによるもののみとなる。各構成要素の運動は全く取り入れられていない。
外部ポテンシャルを導入したことは、エネルギーの寄与をもたらすためというよりは、答えで議論したように、アンサンブルを変えるという意図がある。アンサンブルが変わってしまうことは、次章の例でも同様の問題を見ることができる。詳しくは、299から300ページにかけての議論を参照されたい。
(c). (A18-7.5)-(A18-7.7)式の変換を用いて(A18-7.8)式のよく知っている形まで変形してほしい。
この記事が気に入ったらサポートをしてみませんか?
