構造力学メモ（その８）　コンクリートの割裂引張試験の理論と導出

　コンクリートは、圧縮に強く、引張に弱い材料である。その引張の強度を測定するための試験に割裂引張試験というものがある。
　コンクリートの円柱供試体を側面から押すことで、コンクリート内部に引張応力を発生させ、引張破壊し引張の強度を測定するものである。

図.1 コンクリートの円柱供試体の割裂引張試験

　この試験法では、以下の式によってコンクリートの引張強度を求めることができる。

$$
\sigma_t=\frac{2P}{\pi D L}
$$

　この式の導出は、あまり教科書に載っていない。というのも、それなりに弾性体力学の知識が必要で、本気で説明しようとすると大変で、そこを追求しなくても実験で確認されている以上、上記の式が正しいと認めてしまえば特に実務上問題にはならない。そうはいっても気になる人もいると思うので、この導出について説明していこう。
　もともとのこの割裂引張試験については、昭和18年の以下の論文がもとになっていると言われている。

http://library.jsce.or.jp/jsce/open/00034/29-11/29-11-13144.pdf

　基本的な話は、上記の論文をもとに、割裂引張試験の計算式の導出について紹介する。

１．解くべき方程式（重ラプラス方程式）

　2次元の応力状態（平面応力状態）で重力等の物体力を無視した場合を考えると、応力の平衡方程式は以下のようになる。
　物体力を無視しているのは、今回の事例の場合は、重力等の影響よりも境界面の力＝試験機による荷重のほうがはるかに大きいので問題ない。

$$
\frac{\partial\sigma_x}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}=0\\\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_y}{\partial y}=0
$$

　この方程式は、以下のようなエアリーの応力関数というものを考えれば、自動的に上記の平衡方程式を満たす。

$$
\sigma_x=\frac{\partial^2\phi}{\partial y^2},   \sigma_y=\frac{\partial^2\phi}{\partial x^2},   \tau_{xy}=-\frac{\partial^2\phi}{\partial x\partial y}
$$

　これをひずみの適合条件という以下の式に代入すればいい。

$$
\frac{\partial^2\varepsilon_x}{\partial y^2}+\frac{\partial^2\varepsilon_y}{\partial x^2}-2\frac{\partial^2\varepsilon_{xy}}{\partial x \partial y}=0
$$

　ひずみの適合条件は、ひずみの定義式から導かれる、ひずみ同士の関係式である（$${\partial/\partial x,\partial /\partial y}$$が交換可能なので、この関係式が成立する）。

$$
2\frac{\partial^2\varepsilon_{xy}}{\partial x \partial y}=2\frac{\partial^2}{\partial x \partial y}\frac{1}{2} \left(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\right)=\frac{\partial^2}{\partial y^2}\frac{\partial u_x}{\partial x}+\frac{\partial^2}{\partial x^2}\frac{\partial u_y}{\partial y}=\frac{\partial^2\varepsilon_x}{\partial y^2}+\frac{\partial^2\varepsilon_y}{\partial x^2}
$$

　2次元（平面応力状態）の時の応力とひずみの関係式（構成則）は、等方弾性体の時は以下のようになる。

$$
\varepsilon_x=\frac{1}{E}\sigma_x-\frac{\nu}{E}\sigma_y,   \varepsilon_y=-\frac{\nu}{E}\sigma_x+\frac{1}{E}\sigma_y,   \varepsilon_{xy}=\frac{1+\nu}{E}\tau_{xy}
$$

　これをひずみの適合条件に代入すれば、以下の応力の平衡条件が得られる。

$$
\frac{\partial^2\sigma_x}{\partial y^2}+\frac{\partial^2\sigma_y}{\partial x^2}-\nu\left(\frac{\partial^2\sigma_y}{\partial y^2}+\frac{\partial^2\sigma_x}{\partial x^2}\right)-2(1+\nu)\frac{\partial^2\tau_{xy}}{\partial x \partial y}=0
$$

　ここにエアリーの応力関数を代入すれば、うまいこと$${\nu}$$が消えて、簡単？な数式になる。

$$
\frac{\partial^4\phi}{\partial y^4}+\frac{\partial^4\phi}{\partial x^4}-\nu\left(\frac{\partial^4\phi}{\partial y^2\partial x^2}+\frac{\partial^4\phi}{\partial x^2\partial y^2}\right)+2(1+\nu)\frac{\partial^2\phi}{\partial x^2 \partial y^2}=0
$$

$$
\frac{\partial^4\phi}{\partial y^4}+\frac{\partial^4\phi}{\partial x^4}+2\frac{\partial^2\phi}{\partial x^2 \partial y^2}=0
$$

　この式は、以下のように演算子で表すと、ラプラス演算子の2乗で表される。ラプラス演算子自体が2階微分なので、この方程式は4階の偏微分微分方程式であり、重ラプラス方程式、重調和方程式と呼ばれる。ラプラス演算子が一つの方程式は、ラプラス方程式や調和方程式と呼ばれ、多くの分野で見られる方程式である。
　ラプラス方程式の解は調和関数と呼ばれるが、この重調和方程式の解は、重調和関数と呼ばれる。
　弾性体力学では、このように4階の微分方程式というのはよく出てくる。梁の方程式も4階の常微分方程式であり、板の方程式も4階の偏微分方程式である。

$$
\begin{align*}
\left(\frac{\partial^4}{\partial x^4}+
2\frac{\partial^4}{\partial x^2\partial y^2}+
\frac{\partial^4}{\partial y^4} \right)\phi &=0\\
\left(\frac{\partial^2}{\partial x^2}
+\frac{\partial^2}{\partial y^2} \right)\left(\frac{\partial^2}{\partial x^2}+
\frac{\partial^2}{\partial y^2} \right)\phi &=0\\
\Delta^2 \phi &=0
\end{align*}
$$

２．重ラプラス方程式の二次元極座標表示

　今回考えたいのは、円柱供試体を上下から押したときの応力状態なので、2次元の極座標（円柱座標）$${x=r\cos\theta,y=r\sin\theta}$$で考える必要がある。2次元の極座標（円柱座標）でのラプラス演算子は以下のようになるので、代入すると$${r,\theta}$$の偏微分方程式となる。

$$
\Delta^2 \phi=\left(\frac{\partial^2}{\partial r^2}+\frac{1}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2} \right)\left(\frac{\partial^2}{\partial r^2}+\frac{1}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2} \right)\phi=0
$$

　この偏微分方程式を解くことができれば、2次元の極座標（円柱座標）の応力状態を求めることができる。
　この方程式の一般解の求め方もあるが、ややこしいので、天下り的に以下の$${\phi}$$が解となることを確認する程度にしておく。一般解の求め方はまた別の回に紹介したい。

$$
\phi=-\frac{p}{\pi}r\theta\sin\theta
$$

　係数を無視して$${r\theta\sin\theta}$$が解となるかを確認する。まず1回目のラプラス演算子の計算をすると以下のようになる。

$$
\begin{align*}
\frac{\partial \phi}{\partial r} &=\theta\sin\theta,   
& \frac{\partial^2\phi}{\partial r^2} &=0\\
\frac{1}{r}\frac{\partial \phi}{\partial r} &=\frac{1}{r}\theta\sin\theta,   
& \frac{\partial\phi}{\partial \theta} &=r\theta\cos\theta+r\sin\theta\\   
\frac{\partial^2\phi}{\partial \theta^2} &=-r\theta\sin\theta+2r\cos\theta,   
& \frac{1}{r^2}\frac{\partial^2\phi}{\partial \theta^2} &=-\frac{1}{r}\theta\sin\theta+\frac{2}{r}\cos\theta
\end{align*}
$$

$$
\frac{\partial^2 \phi}{\partial r^2}+\frac{1}{r}\frac{\partial \phi}{\partial r}+\frac{1}{r^2}\frac{\partial^2\phi}{\partial \theta^2} =\frac{2}{r}\cos\theta=\psi
$$

　得られたものを、さらにラプラス演算子の計算を行うと以下のようになり、確かに重ラプラス方程式の解となることが確認できる。

$$
\begin{align*}
\frac{\partial \psi}{\partial r} &=-\frac{2}{r^2}\cos\theta,   
& \frac{\partial^2 \psi}{\partial r^2} &=\frac{4}{r^3}\cos\theta\\
\frac{1}{r}\frac{\partial \psi}{\partial r} &=-\frac{2}{r^3}\cos\theta,   
& \frac{\partial \psi}{\partial \theta} &=-\frac{2}{r}\sin\theta\\
\frac{\partial^2 \psi}{\partial \theta^2} &=-\frac{2}{r}\cos\theta,   
& \frac{1}{r^2}\frac{\partial^2 \psi}{\partial \theta^2} &=-\frac{2}{r^3}\cos\theta
\end{align*}
$$

$$
\frac{\partial^2 \psi}{\partial r^2}+\frac{1}{r}\frac{\partial \psi}{\partial r}+\frac{1}{r^2}\frac{\partial^2\psi}{\partial \theta^2} =\frac{4}{r^3}\cos\theta-\frac{2}{r^3}\cos\theta-\frac{2}{r^3}\cos\theta=0
$$

　ただし、求められるのはエアリーの応力関数なので、そこから応力に変換する式が必要である。弾性体力学や材料力学の教科書によれば、エアリーの応力関数と各応力の関係は以下のようになる。

$$
\begin{align*}
\sigma_r &=\frac{1}{r}\frac{\partial\phi}{\partial r}+\frac{1}{r^2}\frac{\partial^2\phi}{\partial \theta^2}\\
\sigma_{\theta} &=\frac{\partial^2\phi}{\partial r^2}\\
\tau_{r\theta} &=\frac{1}{r^2}\frac{\partial\phi}{\partial\theta}-\frac{1}{r}\frac{\partial^2\phi}{\partial r\partial\theta}=-\frac{\partial}{\partial r}\left(\frac{1}{r}\frac{\partial \phi}{\partial \theta}\right)
\end{align*}
$$

　この関係式は、以下の2次元の極座標（円柱座標）における応力の平衡方程式に代入すれば、この方程式を満たすことが分かる。

$$
\begin{align*}
\frac{\partial\sigma_r}{\partial r}+\frac{1}{r}\frac{\partial\tau_{r\theta}}{\partial \theta}+\frac{\sigma_r-\tau_{r\theta}}{r} &=0\\
\\
\frac{\partial\tau_{r\theta}}{\partial r}+\frac{1}{r}\frac{\partial\sigma_{\theta}}{\partial \theta}+\frac{2\tau_{r\theta}}{r} &=0
\end{align*}
$$

$$
\begin{align*}
\sigma_r &=-\frac{2p}{\pi}\frac{\cos\theta}{r}\\
\sigma_{\theta} &=0\\
\tau_{r\theta} &=0
\end{align*}
$$

　これを$${r,\theta}$$から$${x,y}$$に変換するには、$${-\theta}$$回転すればいいので、以下のように変換すればよい。

$$
\begin{align*}
\sigma_x &=\sigma_r \cos^2(-\theta) +\sigma_{\theta}\sin^2(-\theta)+2\tau_{r\theta}\sin(-\theta)\cos(-\theta)\\
\sigma_y &=\sigma_r \sin^2(-\theta) +\sigma_{\theta}\cos^2(-\theta)-2\tau_{r\theta}\sin(-\theta)\cos(-\theta)\\
\tau_{xy} &=-(\sigma_r-\sigma_{\theta}) \sin(-\theta)\cos(-\theta) +2\tau_{r\theta}\{\cos^2(-\theta)-\sin^2(-\theta)\}
\end{align*}
$$

$$
\begin{align*}
\sigma_x &=\sigma_r \cos^2\theta=-\frac{2p}{\pi r}\cos^3\theta=-\frac{2p}{\pi x}\cos^4\theta\\
\sigma_y &=\sigma_r \sin^2\theta=-\frac{2p}{\pi r} \cos\theta\sin^2\theta=-\frac{2p}{\pi x} \cos^2\theta\sin^2\theta \\
\tau_{xy} &=\sigma_r \sin\theta\cos\theta=-\frac{2p}{\pi r} \sin\theta\cos^2\theta=-\frac{2p}{\pi x} \sin\theta\cos^3\theta
\end{align*}
$$

　$${\phi=-\frac{p}{\pi }r\theta\sin\theta}$$の係数の意味は、以下の図のように考えることができる。応力状態は、原点を中心とした$${r}$$方向の$${\sigma_r}$$しか成分がないので、半径$${r}$$の半円を考えて、その$${x}$$成分の合計を求めればいい。

$$
\begin{align*}
2\int_0^{\pi/2}\sigma_r \cos\theta ds &=2\int_0^{\pi/2}\sigma_r \cos\theta rd\theta\\
&=-4\frac{p}{\pi}\int_0^{\pi/2}\cos^2\theta d\theta\\
&=-2\frac{p}{\pi}\int_0^{\pi/2}(1+\cos2\theta) d\theta=-p
\end{align*}
$$

　$${\phi=-\frac{p}{\pi }r\theta\sin\theta}$$の係数の意味は、原点に作用している荷重$${p}$$を意味していると解釈することができる。

　この解は、地盤工学で出てくるブシネスクの解の線荷重のものと同じものである。

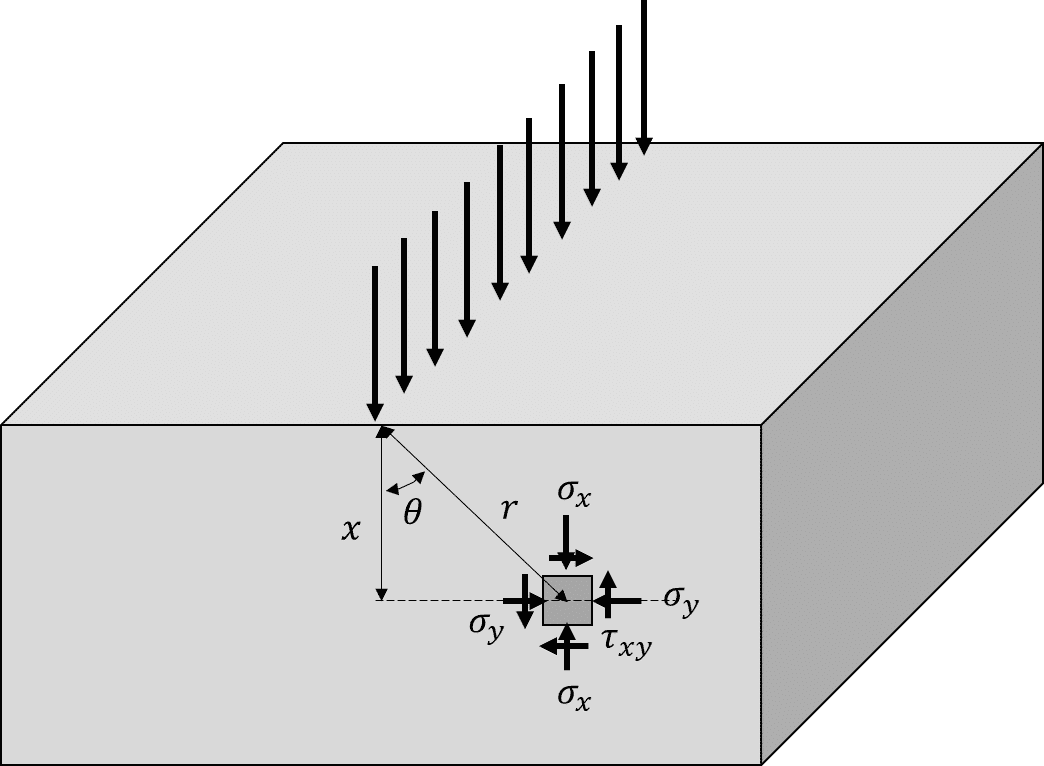
３．割裂引張試験の応力状態

　割裂引張試験は、上下から荷重を受ける。この解だけでは、上からの荷重だけなので、下からの荷重も考える必要がある。
　深さD離れた箇所にも下側から線荷重を与えた場合の応力は以下のようになる（下側の荷重は向きが逆なので、符号が逆になると思うだろうが、荷重によって圧縮応力が発生するので、上側の荷重による応力と符号は同じになる）。

　下側からの荷重による応力は以下のようになる。
（$${\tau_{x'y'}}$$の符号については、$${r',\theta'}$$から$${x,y}$$に戻す時の回転方向が$${r,\theta}$$と逆なので、符号も逆にしている。元の論文と少し変えている）。

$$
\begin{align*}
\sigma_{x'} &=\sigma_{r'} \cos^2\theta'=-\frac{2p}{\pi r'}\cos^3\theta'\\
\sigma_{y'} &=\sigma_{r'} \sin^2\theta'=-\frac{2p}{\pi r'} \cos\theta'\sin^2\theta'\\
\tau_{x'y'} &=-\sigma_{r'} \sin\theta'\cos\theta'=\frac{2p}{\pi r'} \sin\theta'\cos^2\theta'
\end{align*}
$$

　円柱供試体を上下から押した場合の応力状態は、これらの合計と考えられる。円周上の応力状態が0になれば、それは正しいはずなので、円周上での応力状態をチェックしてみる。

$$
\begin{align*}
\sigma_x &=-\frac{2p}{\pi}\left(\frac{\cos^3\theta}{r}+\frac{\cos^3\theta'}{r'}\right)\\
\sigma_y &=-\frac{2p}{\pi}\left( \frac{\cos\theta\sin^2\theta}{r}+\frac{\cos\theta'\sin^2\theta'}{r'} \right)\\
\tau_{xy} &=-\frac{2p}{\pi} \left(\frac{\sin\theta\cos^2\theta}{r}-\frac{\sin\theta'\cos^2\theta'}{r'} \right)
\end{align*}
$$

 　円周上の点は、以下の関係式を満たす$${r,\theta,r',\theta}$$で表される。そこで、それを代入する。

$$
D=r\cos\theta=r'\cos\theta',   \theta+\theta'=90\degree
$$

　円周上での応力状態を求めると、以下のようになる。

$$
\begin{align*}
\sigma_x &=-\frac{2p}{\pi}\left(\frac{\cos^2\theta}{D}+\frac{\cos^2\theta'}{D}\right)=-\frac{2p}{\pi D}\\
\sigma_y &=-\frac{2p}{\pi}\left( \frac{\sin^2\theta}{D}+\frac{\sin^2\theta'}{D} \right)=-\frac{2p}{\pi D}\\
\tau_{xy} &=-\frac{2p}{\pi} \left(\frac{\sin\theta\cos\theta}{D}-\frac{\sin\theta'\cos\theta'}{D} \right)=0
\end{align*}
$$

　すると、円周上では、応力状態が$${\sigma_{x}=-\frac{2p}{\pi D},\sigma_{y}=-\frac{2p}{\pi D},\tau_{xy}=0}$$となってしまい、$${\sigma_x,\sigma_y}$$に余分な圧縮力が入ってしまっていることになる。
　つまり、この応力状態の解は、供試体の円周上で垂直応力が0になるという境界条件を満たしていないことになる。
　そこで、$${\sigma_x,\sigma_y}$$に$${\frac{2p}{\pi D}}$$を加えて、打ち消せば、境界条件を満たす解となる。

$$
\begin{align*}
\sigma_x &=-\frac{2p}{\pi}\left(\frac{\cos^3\theta}{r}+\frac{\cos^3\theta'}{r'}\right)+\frac{2p}{\pi D}\\
\sigma_y &=-\frac{2p}{\pi}\left( \frac{\cos\theta\sin^2\theta}{r}+\frac{\cos\theta'\sin^2\theta'}{r'} \right)+\frac{2p}{\pi D}\\
\tau_{xy} &=-\frac{2p}{\pi} \left(\frac{\sin\theta\cos^2\theta}{r}-\frac{\sin\theta'\cos^2\theta'}{r'} \right)
\end{align*}
$$

　この式から、$${x}$$軸、すなわち$${y=0\rightarrow \theta=0,\theta'=0}$$のときの応力状態を求めれば、圧縮している方向と垂直な方向に引張応力が発生し、その値は$${x}$$軸上で一定の値$${\frac{2p}{\pi D}}$$であることが分かる。

$$
\begin{align*}
\sigma_x(\theta=0,\theta'=0) &=-\frac{2p}{\pi}\left(\frac{1}{x}+\frac{1}{D-x}\right)+\frac{2p}{\pi D}\\
\sigma_y(\theta=0,\theta'=0) &=\frac{2p}{\pi D}\\
\tau_{xy}(\theta=0,\theta'=0) &=0
\end{align*}
$$

　$${x=0,D}$$で解が発散してしまうので、この解は、数学的には正しいが、物理的には正しくない。そのあたりを修正した理論もあるが、さらに話がややこしくなる。

　荷重は$${P}$$で、円柱供試体の長さは$${L}$$なので、線荷重は$${p=P/L}$$となって、それを上記に代入すれば、求めたかった式を得ることができる。

$$
p=P/L   \rightarrow   \sigma_y(\theta=0,\theta'=0)=\frac{2P}{\pi DL}
$$

４．おわりに

　コンクリートの割裂引張試験という、方法自体は簡単な試験だが、その引張応力を求める式は、2次元の弾性体力学をふんだんに使っている難しい話が背景にあることが理解できたかと思う。
　このような難しい話が、すでに昭和18年には求められていたというから驚くべきことだと思う（18世紀には、数学が相当高度なレベルになっていたことを考えると、それほどすごくない、という意見もあるかもしれないが）。

　途中、重ラプラス方程式の解を天下り的に与えたが、こちらの求め方については、今後記事にしていきたい。