VaR算出について

アイアンコンドルメインの投資を行うにあたり、VaRを取り入れて投資しています。ここでは、エクセルで算出する方法を記載したいと思います。

はじめに

VaRとは、Value asset Riskのことであり、
①観測機関の変動データをもとに、
②将来の一定保有期間のうちに、
③ある一定の信頼区間でとりうる値幅
を統計的に推定した値のことを指します。
簡単にいうと、過去のデータから未来の取りうる変動幅を予測することです。

方法

方法は大きく以下の３つに分けられます。
①分散共分散法
⇒リスク感応度（⊿）が一定の反応を示す前提で行う算出法。算定がかなり楽です。
②モンテカルロ・シュミレーション法
⇒乱数を用いて信頼区間を決める方法です。エクセルでも十分算定可能ですので、こちらも楽です。
③ヒストリカル法
⇒過去の数字から推定する方法ですが、エクセルでデータをまとめるのがとても苦です。

今回①と②を比べてみましたが、大差はありませんでした。そこで、より実際の相場感に近い②を採用したいと思います。

ここで大切なのは、標準偏差の範囲についてです。
直近１か月を範囲とした場合では、仮に前月価格変動が小さかった場合は当該月のVaRも狭くなり、いざというときの被害が大きくなりそうです。同じことは年単位でも言えました。
そこで、今回はコロナ暴落を含めた2020～2022年の３か年の平均標準偏差を採用します。

具体的計算方法

１　日経平均のデータを抽出
私は以下のサイトからエクセルをダウンロードしています。見やすくて便利。

ダウンロードセンター － 日経平均プロフィル

２　期間の変動率を算出
例えば、20日後に価格がどの程度変動しているかを知りたいときは、［n日価格-(n+19)日価格］/n＝Aで変動率を示すことができます。
このAをX個計算し、その標準偏差（SD)を求めます。
※正確には角変換が必要ですが、おおよそ近い値となるので、今回はこのまま説明します。
この標準偏差（SD）のX個の値を平均した値Yを、モンテカルロシュミレーションを用いて乱数を発生させます。

３　モンテカルロ・シュミレーション
'=Y*NORMSINV(RAND())'が乱数発生の式となります、このYに数字を入れ、ずらーっと10,000個ほどセルをコピーして作成します。
※10.000である必要性はないのですが、1,000では偏りが大きく、100,000など大きくすると作業がとても煩雑なので、中庸で10,000としています。

この数群をヒストグラムにすると以下のようになるかと思います。

ここで、例えば99% VaRを求めたいときは、乱数の100番目の数字と900番目の数字が、変動幅の許容範囲となります。

結果

実際に25日ベースで、2020～2022年の99% VaRを算出してみました。

乱数:モンテカルロ・シュミレーションを行う際の数の総和

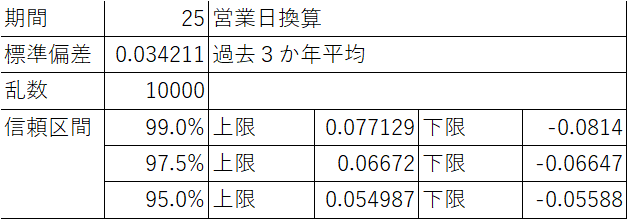
期間を25日(約1ヶ月)とした場合、1ヶ月後の値幅は信頼区間99％の場合±約8％となります。例えば、1/1に日経が27000円とすると、2/1には29160〜24840円の範囲に99％の確率で着地すると言えます。
しかし、下限については暴落リスクをより反映させるため、オプションのデルタ値から係数を導き、おおよそ-8%×1.5～2倍数値を採用した方が無難そうです。
それを加味すると、27000の場合、29160〜22680円が99%信頼区間での推定VaRと言えます。

終わりに

すごいわかりにくいと思います、すみません。
以下の２サイトがもっと詳しく記載しているので参考に貼ります。

わかりやすい概要があります。

http://www.ffr-plus.jp/material/pdf/0006/risk_meter_quantification_03.pdf

エクセルの計算方法が詳しくあります。
https://www.sigmabase.co.jp/useful/monte/index.html