
【STATA Techs-006】相関係数と単回帰分析
THEME:相関係数と単回帰分析
GOAL:STATAで相関係数を返せるようになる。単回帰分析ができるようになる。
◯サンプルデータ◯
◯使用コマンド◯
correlate varname1 varname2
:2変数の相関係数を返す
※「correl」だけでも可
※correl varname1 varname2 varname3 …varnamen
:n変数の相関行列を返す
reg varname1 varname2
:varname1を被説明変数(y)、varname2を説明変数(x)とした時の単回帰分析を実行し、回帰係数等を返す
◯やり方◯
今回は相関係数を返した上で、単回帰分析をやってみます。
①相関係数・相関行列
まずは、サンプルデータ(「sample2」)の戸主の年齢(「age_master」)と戸主所得(「income_master」)を使って、2変数の相関係数を返しましょう。コマンドは以下のとおりです。
correl age_master income_master
correlコマンドによって「age_master」と「income_master」の相関係数が返すことができました。相関係数(r)は以下のような特徴を持ちます。
rは-1から1までのいずれかの値をとる
|r|が1に近いほど相関関係が強く(プラス1に近ければ「正の相関」、マイナス1に近ければ「負の相関」)、0に近いほど相関関係が弱い(「無相関」)
|r|が0に近くても、何らかの関係がある場合がある
rは単位を持たない値であり、データの単位がどのようなものであっても計算できる
今回は、r=0.0573なので無相関のようです。散布図(twoway scatterコマンド)を描いて確認してみましょう。
twoway scatter income_master age_master
確かに、右肩上がりにも右肩下がりにもない無相関の散布図のようです。では、他の変数はどうでしょうか。相関行列で確認してみましょう。コマンドは以下です。
correl num_householdmembers eduyear_master age_master exp_master area income_master income_household capital_household
相関行列をすると、任意の変数がなんの変数と関係がありそうか一目でわかります。
②相関行列のヒートマップ化
これをグラフィック化(ビジュアライズ)してみましょう。まず、以下の3つのパッケージをインストールします。
ssc install heatplotssc install palettes, replace ssc install colrspace, replaceインストールできましたか?その後、もう一度、相関行列を行い、ヒートマップを表示させてみましょう。
correl num_householdmembers eduyear_master age_master exp_master area income_master income_household capital_household
heatplot corrmatrix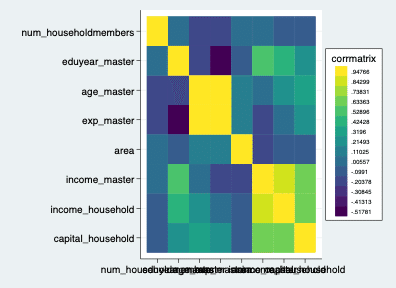
そうすると、こういったヒートマップが返されます。相関係数が高いほど暖色に、低いほど寒色になっています。これだけでも良さそうですが、それぞれのブロックに相関係数は入れたいですね。次はこのコマンドを走らせてみましょう。
heatplot corrmatrix, values(format(%4,3f) size(medium)) legend(off)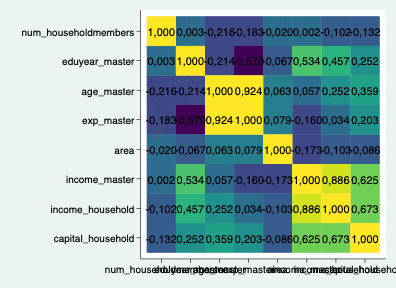
おっと、字が大きすぎたようです。その場合は、「size(medium)」を「size(small)」にしてみます。ちなみに、コマンドの中身について、「format(%4,3f)」の%4は固定値ですが、3fは「小数点何まで表示するか」を指定します。例えば、2fですと小数点2までが返されます。「legend」はonにすると色の濃淡を示すスケールが付されます。
heatplot corrmatrix, values(format(%4,3f) size(small)) legend(on)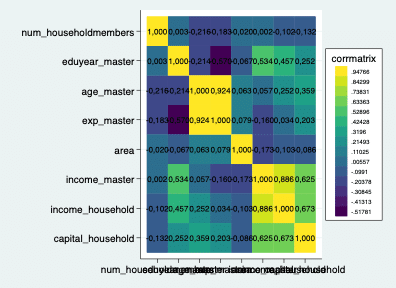
良さそうですね!次は、ヒートマップ下部の字が重なってしまっている場所をどうにかしたいですね。この場合は図の「aspectratio」とx軸ラベルの「angle」で調整します。コマンドは以下です。「aspectratio」は1を下回ると横長になり、1以上ですと縦長になります。「angle」はx軸ラベルの字に角度をつけるものです。
これで見栄えのいいヒートマップができましたね。
heatplot corrmatrix, values(format(%4,3f) size(small)) legend(off) aspectratio(0.5) xlabel(,labsize(small) angle(45)) ylabel(,labsize(small))
③単回帰分析
次に、単回帰分析をしてみましょう。単回帰分析分析の式は以下でした。
y = β0 + β1x + u
*β0は切片、β1xは説明変数、uは誤差

これを踏まえ、単回帰分析を走らせます。今回は、戸主の経験年数(「exp_master」)を被説明変数、戸主の年齢(「 age_master」)を説明変数にとってみます。式は以下です。regressionコマンドの直後に被説明変数yがきて、その後説明変数xがきますので、reg + exp_master + age_masterという順になります。
reg exp_master age_master
なんかたくさん出てきましたね。見るべきもののみを抽出します。
・Number of obs:観測数
・R-squared:決定係数(相関係数の2乗)=回帰分析の当てはまり具合
・Adj R-squared:自由度調整済み決定係数
・Coef.:推定係数
・Std.Err:標準誤差
・P>|t|:P値=仮説検定(自分が設定した仮説が正しいかどうかを統計的に判定する方法)において、元データの指標が、サンプルから観察された値と等しいか、それよりも大きな(小さな)値をとる確率)
・95% Conf. Intervall:95%信頼区間
・_cons:切片
これを踏まえると、先の式は以下のように書き換えられます。
exp_master = -20.42 + 1.099*age_master + u
推定係数は1.099で、右肩上がりの回帰式が得られました。また、P値はいずれも0.000で1%水準で有意のようです。また、決定係数は0.85と高く、精度の良い単回帰式のようです。本当にそんな正の相関があるのでしょうか。最後は実際に散布図を確認してみましょう。赤いラインが単回帰線です。
twoway scatter exp_master age_master || lfit exp_master age_master
exp_masterの推定値を出したいときは、一次関数(y = ax + b)の要領と同じで、以下の式のage_masterに任意の数値を代入します。
exp_master = -20.42 + 1.099*age_master
例えば、agemasterが30であれば、exp_masterの推定値は
exp_master = -20.42 + 1.099*30 = 32.97 - 20.42 = 12.55
ということになります。逆にage_masterの推定値を出したいときは、式変形をしてから代入します。
exp_master = -20.42 + 1.099*age_master
1.099*age_master = exp_master -20.42
age_master = exp_master/1.099 - 20.42/1.099
age_master = exp_master/1.099 - 18.58
となりますので、ここのexp_masterに任意の数字を代入します。例えば60であれば、age_masterは36.01でしょうか。
しかし、いちいち一次式に代入して手計算するのは面倒だと思います。もちろんオートマでやる方法あります。手順は以下です。
・predict [新変数]
→predictコマンドの後、新しい変数が作成されているか確認
・list [β1xにしていた変数] [さっき作った新変数] in 1/X
→「in 1/X」は予測値を何件表示させるかを指示。Xに100を入れれば100件表示される
predict y_hat_exp_master
list age_master y_hat_exp_master in 1/10
④色々な単回帰のグラフ
ここでは今あるデータだけを使って、色々なグラフを作ってみましょう
A)y=ax+bの線形予測のみ
y=ax+bの線形予測。フィット線のみ描画されます。
twoway lfit income_master age_master
なお、直線の線形予測ではなく、2次式、つまりxおよびx^2でのyの回帰から、yの予測を計算するのであれば、「lfit(liner fit)」ではなく「qfit」、フラクショナル多項式として表示させるのであれば「fpfit(fractional polynomial fit)」にします。
twoway fpfit income_master age_master
B)データのプロット付き線形予測(カテゴリごと)
カテゴリ変数の値ごとにグラフを作成し、合計のフィット結果もグラフ化します。
twoway scatter income_master age_master || lfit income_master age_master ||, by(area, total row(1))
twoway scatter income_master age_master || fpfit income_master age_master ||, by(area, total row(1))
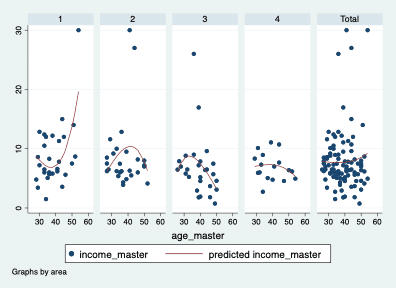
C)データのプロット&信頼区間付き線形予測
フィット線と信頼区間をプロットします。Aとの違いは、Aで「lfit」だったものが「lfitci」になっているのみです。
twoway lfitci income_master age_master
twoway fpfitci income_master age_master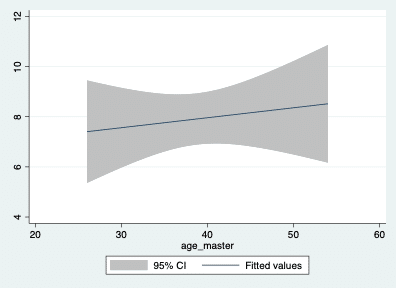

D)データのプロット&信頼区間付き線形予測
データポイントの散布図、フィット線、信頼区間をプロットします。
twoway lfitci income_master age_master || scatter income_master age_master
twoway fpfitci income_master age_master || scatter income_master age_master

ここで注意ですが、上のコマンドは、twoway lfitci 〜を先に指示し、その上にプロット(scatter)を重ねるようにコマンドしています。逆に、いつも通りtwoway scatter〜としてしまうと、以下のような形で、プロットの上に95%信頼区間の帯が配置されてしまいます。
twoway scatter income_master age_master || lfitci income_master age_master
E)データのプロット&信頼区間付き線形予測(カテゴリごと)
任意のカテゴリごとに作成するのは、Bの時と要領は一緒で、「||, by(varname, total row(1))」を最後に添えるだけです。
twoway lfitci income_master age_master || scatter income_master age_master ||, by(area, total row(1))
twoway fpfitci income_master age_master || scatter income_master age_master ||, by(area, total row(1))

======
本田恒平(Kohei Honda)
一橋大学大学院経済学研究科博士後期課程(政治経済学、労働政策)
▼質問やご意見等はコメントかホームページのフォームから▼
