
PyTorch深層学習⑥線形回帰:理論編
前回は、データセットについて解説しました。今回は線形回帰を行うモデルについて理論を解説します。
線形回帰は、さまざまなモデルを理解する上での基本となります。
本シリーズの記事リスト
⑥線形回帰:理論編
線形回帰のモデルを通して、モデルを訓練するとはどういうことなのかを理解しましょう。
線形回帰
線形とは
$${y}$$と$${x}$$の間に次の関係があるとします。
$$
y = a x + b
$$
ここで$${a}$$と$${b}$$は定数です。このような$${y}$$と$${x}$$の関係を線形と呼びます。
例えば、$${a = \frac{1}{2}}$$と$${b = 1}$$ならば下図のようになります。

つまり、直線の関係になっています。
また、$${x}$$を説明変数とか独立変数と呼びます。また、$${y}$$を目的変数とか従属変数と呼びます。これらの呼び名には$${x}$$の値によって$${y}$$が決まるという意味や、$${x}$$の値を変えると、それに従って$${y}$$が動くといった意味が込められています。
また、$${x=0}$$における$${y}$$の値を切片(intercept)、$${x}$$を1増加させた時の$${y}$$の変化率を直線の傾き(slope)と呼びます。

また、$${y = f(x)}$$という表記をして$${y}$$が$${x}$$の関数であると呼びます。特に線形の関係を持つ関数は線形関数と呼びます。また、$${f}$$は function からきていますが、$${g}$$とか$${h}$$とか必要に応じて異なるアルファベットを使ったりします。
線形関数は、独立変数が一つであるとは限りません。例えば、2つの独立変数を持つ線形関数$${f(x, y)}$$を考えます。
$$
z = f(x, y) = 1.5 x + 0.7 y
$$
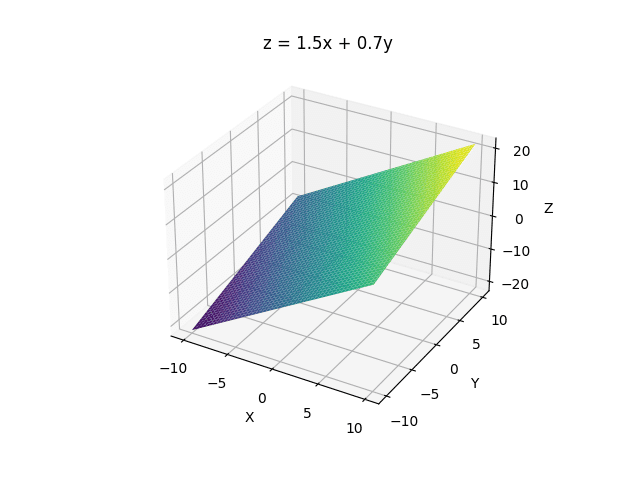
二つの独立変数だと平面が現れます。これも線形と呼びます。以下のプログラムで生成しました。
import numpy as np
import matplotlib.pyplot as plt
# データ生成
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
Z = 1.5*X + 0.7*Y
# 3次元の図
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('z = 1.5x + 0.7y')
# プロットの表示
plt.show()独立変数をいくら増やしても線形の関数を作ることができます。つまり、独立変数と従属変数の関係として、各独立変数に固定の係数(傾き)があり、最後に固定の値(切片、バイアス)がある場合は「線形」とみなされます。
$$
y = f(x_1, x_2, \dots, x_N) = w_1 x_1 + w_2 x_2 + \dots + w_N x_N + b
$$
ここからは、独立変数が一つのケースで話を進めます。
ベストフィット
データが綺麗な線形になっているとは限りません。大抵はノイズがあったりしてサンプルデータには多少の散らばりがあります。
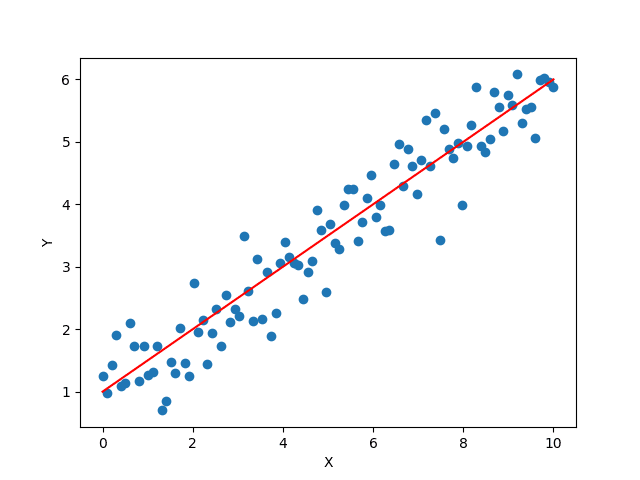
例えば、次のような散布図があるとします。

ここに線形の関係があるのは一目瞭然です。しかし、たくさんの線形関数で近似できそうです。

$${y=ax+b}$$でデータを近似するとした場合、傾き$${a}$$と切片$${b}$$をどのように選ぶかによってどのくらいよくデータを説明できているかが変わってきます。
たくさんある線形関数の内もっともデータをうまく説明(近似)できるものをベストフィット(Best fit)と呼びます。
ベストフィットであるかどうかは、データの値と線形関数による予測値との誤差の値を見て判断します。そこで損失関数が登場します。
損失関数
ディープラーニングを含む機械学習では、さまざまな損失関数(ロス関数)があります。損失関数は、モデルが予測した値と実際のデータの値との違いを数値として表現します。損失関数が返す値を損失値と呼び、エラーが大きいほど損失値は大きくなります。
MSE(平均二乗誤差)
線形関数でデータを説明する場合は、損失関数として平均二乗誤差(Mean Squared Error、MSE)がよく使われます。
$$
\text{MSE} = \dfrac{1}{N} \sum\limits_{i=1}^N (y_i - \hat{y_i})^2
$$
ここで、$${y_i}$$は$${x_i}$$に対応するデータの値、$${\hat{y}_i}$$は$${x_i}$$に対応する線形関数による予測値になります。よって、$${(y_i - \hat{y_i})}$$は$${x_i}$$における近似の誤差になります。
誤差の二乗を計算することで、誤差が非負(0か正)の値になります。また、誤差が大きいほど二乗による値がより大きくなります。
このMSEを最小化することができれば、線形関数によるベストフィットを見つけたことになります。そのためには、MSEが小さくなるようにパラメータ$${a}$$と$${b}$$を調整していく必要があります。
ちなみに、解析的に(つまりは計算をして)MSEを最小化するパラメータを見つけることも可能です。しかし、ここではパラメータを少しずつ調節する手法を使います。なぜなら、ディープラーニングなどニューラルネットワークの訓練ではこの方法がよく使われるからです。
そのような手法を勾配降下法と呼びます。
MSEの勾配
データ$${y_i}$$と線形関数(モデル)の予測値$${\hat{y}_i = a x_i + b}$$を使って損失関数を計算するので、損失関数をパラメータ$${a}$$と$${b}$$の関数とみなすことができます。
$$
\text{MSE}(a, b) = \dfrac{1}{N} \sum\limits_{i=1}^N \left(y_i - (a x_i + b) \right)^2
$$
$${x_i}$$と$${y_i}$$は与えられたものであり固定されています。つまり、我々が変更できるのは近似に使い線形モデルのパラメータだけです。
よって、MSEの偏微分を$${a}$$と$${b}$$に対して計算することができます。$${a}$$によるMSEの偏微分は次のように表記します。
$$
\dfrac{\partial \text{MSE}(a, b)}{\partial a}
$$
これは$${a}$$以外のパラメータ(ここでは$${b}$$)を固定した場合の$${a}$$によるMSEの変化率を計算しています。つまり、$${a}$$の値を1増やした場合にMSEによる損失値がどのくらい変わるのかを表現しています。
同様に、$${b}$$によるMSEの偏微分は次のように表記します。
$$
\dfrac{\partial \text{MSE}(a, b)}{\partial b}
$$
これらの偏微分を手で計算することは可能ですが、これはPyTorchがやってくれるので我々が計算する必要はありません。
ちなみに次のようになります。
$$
\frac{\partial \text{MSE}(a, b)}{\partial a} = \frac{2}{N} \sum\limits_{i=1}^N (y_i - \hat{y}_i)(-x_i)
$$
$$
\frac{\partial \text{MSE}(a, b)}{\partial b} = \frac{2}{N} \sum\limits_{i=1}^N (y_i - \hat{y}_i)(-1)
$$
また、全てのパラメータによる偏微分を一つのベクトルとしてまとめたものを勾配(Gradient)と呼びます。
$$
\text{grad} \ \text{MSE} = \nabla \text{MSE} = \left[ \dfrac{\partial \text{MSE}}{\partial a}, \dfrac{\partial \text{MSE}}{\partial b} \right]
$$
grad は Gradient から来ています。記号としては$${\nabla}$$(ナブラ)をよく使います。
訓練
線形関数を使った近似モデルによる予測の誤差を小さくすることでモデルをより正確にすることができます。このことをデータからモデルが学習していると捉えます。あるいはデータでモデルを訓練するとも呼びます。
SGDオプティマイザ
オプティマイザ(Optimizer)は最適化(Optimization)を行う機能を持ちます。オプティマイザは勾配を利用してパラメータの更新を行います。
勾配、つまり各パラメータに関する損失関数の偏微分がわかると、偏微分の値が正か負であるかによって、パラメータの値を増加させるのか減少させるのかが決まります。
$${\dfrac{\partial \text{MSE}}{\partial a} > 0}$$ なら $${a}$$を減少させる
$${\dfrac{\partial \text{MSE}}{\partial a} < 0}$$ なら $${a}$$を増加させる
$${\dfrac{\partial \text{MSE}}{\partial b} > 0}$$ なら $${b}$$を減少させる
$${\dfrac{\partial \text{MSE}}{\partial b} < 0}$$ なら $${b}$$を増加させる
例えば、$${a}$$を更新する式は次のようになります。
$$
a \leftarrow a - \alpha \dfrac{\partial \text{MSE}}{\partial a}
$$
ここで$${\alpha}$$は学習率です。更新の度合いをコントロールするために小さな値を指定します。学習率については、0.01や0.001やもっと小さい値などが考えられますが、モデルの特性やパラメータの数などによって人間が決める必要のあるハイパーパラメータ(Hyper-parameter)になります。
$${b}$$の更新式は次のようになります。
$$
b \leftarrow b - \alpha \dfrac{\partial \text{MSE}}{\partial b}
$$
よって、両方の更新式を次のようにまとめることができます。
$$
\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \nabla \text{MSE}
$$
ここで$${\boldsymbol{w} = (a, b)}$$としています。
このような更新式を使うオプティマイザを確率的勾配降下法オプティマイザ(Stochastic Gradient Descent Optimizer, SGD Optimizer)と呼びます。単にSGDと呼ぶこともよくあります。
パラメータの更新
線形モデルの訓練をまとめると以下の図になります。

まず、線形モデルのパラメータ$${a}$$と$${b}$$を何らかの値に初期化します。例えば、$${a=1}$$と$${b=0}$$とします。
そして、$${x_i}$$を使って予測値$${\hat{y}_i}$$を計算します。データが少なければ、全ての$${x_i}$$で予測を計算します。多ければバッチにして分けたものに対して予測を計算します。この過程をフィード・フォワード(Feed Forward)と呼びます。
次に、損失関数を使って損失値を計算します。これに対して勾配を計算し、オプティマイザを使ってパラメータの更新をします。この時に学習率が使われます。
更新されたパラメータを使って、再びフィード・フォワードを行い、前回と同じ工程を通して再びパラメータを更新します。
パラメータが更新されていくと損失値が小さくなっていくので、損失値があまり変化しなくなったら、収束したとみなして訓練を終了します。
うまくいけばベストフィットな線形モデルになります。
まとめ
今回は線形関数を使ったモデルによる学習の過程を解説しました。ディープラーニングを含む、あらゆるニューラルネットワークの学習で同様の過程が使われます。
なお、オプティマイザについてはSGDだけでなく、色々と種類がありますが、単純なので今回はSGDを使った説明を行いました。
次回は実際にPyTorchで線形モデルの学習を実装します。
(続く)
この記事が気に入ったらサポートをしてみませんか?
