
学習率の最適化
学習目標
ディープラーニングの学習に用いられるアルゴリズムである勾配降下法を理解する。そして勾配降下法にはどのような課題があり、どうやって解決するかを理解する。
勾配降下法
勾配降下法の問題と改善
キーワード:学習率、誤差関数、交差エントロピー、イテレーション、エポック、局所最適解、大域最適解、鞍点、プラトー、モーメンタム、AdaGrad、AdaDelta、RMSprop、ADAM、AdaBound、AMSBound、ハイパーパラメータ、ランダムサーチ、グリッドサーチ、確率的勾配降下法、最急降下法、バッチ学習、ミニバッチ学習、オンライン学習、データリーケージ
損失関数
損失関数
機械学習では、モデルの予測値と実際の値との誤差をなくすことを目指します。誤差を数学的に表現したものが誤差関数です。扱う問題によって異なる誤差関数が使われます。
回帰問題では平均二乗誤差が使われますし、分類問題であれば交差エントロピーが使われます。誤差という言葉が回帰問題を連想させるので、より一般的に損失関数と呼ぶことも多いです。
最小化問題
損失値を下げるのが機械学習における訓練の目的だとすると、数学的には関数の最小化問題になります。関数が最小になる値では関数の微分あるいは偏微分がゼロになり、簡単な数式だと解析的に計算できます。
例えば、$${y = x^2}を$${x}$$で微分すると$${y′= \frac{dy}{dx} = 2x}$$なので$${x = 0}$$で微分が0になります。
厳密には微分がゼロになるのは関数の最大値あるいは最小値です。最小値であることを確認するためには、2階微分が正であることを確認する必要があります。
また、パラメータが複数ある場合は微分でなく偏微分を計算します。その際に、鞍点(一つのパラメータでは極小だが、他のパラメータでは極大)が生じる可能性もあります。

大域最適解と局所最適解
微分・偏微分で求めた解は大域最適解(関数全領域における解)であるとは限らず、ある範囲における局所最適解である可能性もあります。

解析的に解ける問題では、全ての最適解を計算して最小になる解を選ぶ必要があります。しかし、次に述べるようにディープラーニングでは解析的な手法が使えません。
勾配降下法
ディープラーニングで使用するディープニューラルネットワークはパラメータである重みが多数あり、巨大な関数と考えられます。また、損失値を計算するためのデータも莫大にあります。よって、ディープラーニングの損失関数の最小値を解析的に解くのは現在のテクノロジーでは困難です。
そこで、損失値が小さくなるような操作を繰り返すこと(イテレーション)によって少しずつ解に近づく方法が使われます。
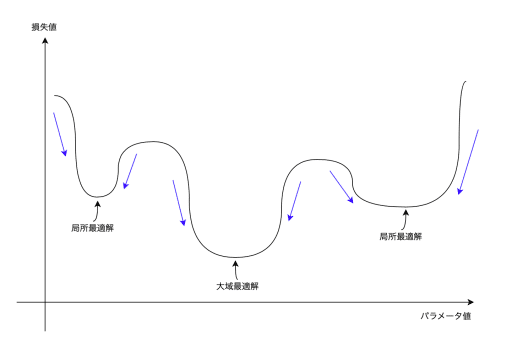
これを勾配降下法(gradient descent method)と呼びます。勾配降下法は勾配にそって関数が最小になる点を探索するアルゴリズムです。パラメータ(重み)を少しずつ更新して損失関数を最小化します。
学習率
一度に更新する度合いを学習率と呼び、勾配に沿った移動を調節します。
更新の度合いは以下のように決まります。
$$
\theta_{t+1,i} = \theta_{t,i} \ – \ \eta \, g_{t,i}
$$
tは学習のステップ。t+1はtの次のステップ
iはパラメータのインデックス
$${\theta_{t+1,i}}$$はステップt+1でのパラメータiの値(θのカタカナ表記はセータ)
$${\theta_{t,i}}$$はステップtでのパラメータiの値
$${\eta}$$は学習率($${\eta}$$のカタカナ表記はエータ)
$${g_{t,i}}$$はステップtにおける損失関数をパラメータiで偏微分(gは勾配:gradientの最初の一文字)
損失関数Lは全てのパラメータと入力データに依存し、偏微分は$${g_{t,i} = \frac{\partial L}{\partial \theta_{t,i}}}$$
後述しますが、学習率$${\eta}$$を調節する手法がいろいろとあります。
エポックとバッチサイズ
勾配降下法では訓練データを使って損失値を計算しパラメータの更新を続けていきます。この際、訓練データを何周もしてくのが通常ですが、この1周をエポックと呼びます。訓練データを10周するならエポックが10あることになります。
また、勾配降下法は一回の更新で使用するデータによって3つに区別されます。また、一回に使用するデータの数をバッチサイズと呼びます。

勾配降下法の問題と改善
SGD
SGD(Stochastic Gradient Descent)は最も基本的なパラメータの更新方法です。
$$
\theta_{t+1,i} = \theta_{t,i} \ – \ \eta \, g_{t,i}
$$
勾配降下法では、局所最適解を避ける必要があります。一つの方法として、学習率ηを大きく設定することが考えられます。これによって山を越え他の最適解へと移動するチャンスが増えます。ただし、学習率を徐々に小さくするなどの工夫が必要となります。さもないと、いつまでも最適解が固定されません。
また、学習率はハイパーパラメータなので人間の手によって決める必要があります。ランダムサーチやグリッドサーチを駆使してさまざまな学習率で実験したりと時間がかかります。
ハイパーパラメータの調節は検証用データを使ってモデルの精度を確かめながら行うのですが、あまりに過ぎるとデータリーケージが起こり、検証用データでは良い性能が出ても評価(テスト)データによる汎化性能が悪くなってしまうので気をつける必要があります。
以上より、訓練中に検証用データを用いることなく自動で調節できる学習率があれば便利なのがわかります。
モーメンタム
前述したように勾配降下法では、何らかの方法で鞍点を避ける必要があります。ディープニューラルネットワークではパラメータの数が多く、鞍点が発生する可能性が高くなっています。特に鞍点の周りの勾配が小さく平坦になっていると、そこから抜け出すのが難しくなります。このような状態にあることをプラトーと呼びます。
鞍点を避ける方法としてMomentum(モーメンタム)があります。モーメンタムは物理からの慣性の考えを利用したものです。現在の勾配に過去の勾配からの勢いを合わせたものを使ってパラメータのアップデートを行うので更新の方向が慣性のように継続する効果があります。
モーメンタムの更新は以下のように行います。
$$
v_{t,i} = \gamma v_{t-1,i} \ - \ \eta \, g_{t,i}
$$
$${\gamma}$$では0.9などの値が使われます。パラメータの更新は以下になります。
$$
\theta_{t+1,i} = \theta_{t,i} + v_{t,i}
$$
しかし、モーメンタムには慣性による移動が行きすぎる傾向があります。慣性はやがては落ち着いていきすぎても戻ってくるのですが、なるべくいきすぎない方法が次のNesterovによるものです。
Nesterov
Nesterovの加速勾配法はモーメンタムに変更を加え慣性による行き過ぎを軽減します。そのアイデアは簡単で、慣性による移動をパラメータに適用してから、勾配による移動を加えます。
$$
\begin{align*}
\theta_{t', i} &= \theta_{t,i} + \gamma v_{t-1, i} \\
\theta_{t+1,i} &= \theta_{t',i} - \eta \, g_{t',i}
\end{align*}
$$
つまり、慣性によるパラメータの移動を行った後に勾配を計算します。勾配が下がる方向に向かって慣性で動いているときは動いた先の勾配が小さくなっているので行き過ぎを軽減できるというわけです。
AdaGrad
AdaGrad(Adaptive Gradient Algorithm)は学習率を自動で各パラメータごとに調節します。2011年に発表されました。
$$
\theta_{t+1, i} = \theta_{t,i} - \frac{\eta}{\sqrt{G_{t, ii} + \epsilon}} g_{t,i}
$$
$${G_{t,ii}$$は、パラメータiiの過去の全ての勾配の2乗の和です。$${\epsilon}$$はゼロの割り算にならないように小さな固定値(例えば、$${1.0e^{−10}}$$)を指定します。
大きな勾配による変更が続くパラメータの学習率はどんどん小さくなります。よって、勾配の小さいパラメータの学習率が比較的大きくなり全体として学習を加速するのが狙いです。
問題点としては$${G_{t,ii}}$$が常に増加していくので学習率がどんどん小さくなって効果がなくなってしまうことです。$${\eta}$$の値を多少変えたとしても学習率が小さくなっていくことに変わりはありません。
AdaDelta
AdaDeltaはAdaGradをベースに学習率がどんどん小さくなってしまう問題を解決しました。2012年に発表されました。
勾配の2乗の指数移動平均 $${E[g^2]_{t,i}}$$を$${G_{t,ii}}$$の代わりに使います。
$$
E[g^2]_{t,i} = \gamma E[g^2]_{t−1,i} + (1 \ – \ \gamma) g^2_{t,i}
$$
モーメンタムと似た考えで$${\gamma}$$によって過去の勾配の影響を継続していきます。$${\gamma}$$には0.9がよく使われます。
よってパラメータの更新式は以下になります。
$$
\theta_{t+1, i} = \theta_{t,i} - \frac{\eta}{\sqrt{E[g^2]_{t,i} + \epsilon}} g_{t,i}
$$
$${E[g^2]_{t,i}}$$では遠い過去に起きた勾配の影響がなくなっていくので学習率がどんどん小さくなるという問題が起こりにくくなっています。
次に、分母は勾配の2乗平均平方根(RMS)なのでそれをRMS[g]t,iRMS[g]t,iと表記します。
$$
\theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{RMS[g]_{t, i}} g_{t,i}
$$
SGDやモーメンタムやAdaGradでもそうですが、右辺と左辺の単位があっていません。そのためパラメータの変更(デルタ)の2乗の指数移動平均を計算し、その平方根を$${\eta}$$の代わりに使うことで単位を合わせます。
$$
E[\Delta \theta^2]_{t,i} = \sqrt{E[\Delta \theta^2]_{t,i} + \epsilon}
$$
よって、パラメータのデルタの2乗平均平方根は以下のようになります。
$$
RMS[\Delta \theta]_{t,i} = \sqrt{E[\Delta \theta^2]_{t,i} + \epsilon}
$$
更新時tでは$${RMS[\Delta \theta]_{t,i}}$$の値は分からないので$${RMS[\Delta \theta]_{t-1,i}}$$で代用します。全てをまとめると以下になります。
$$
\theta_{t+1,i} = \theta_{t,i} - \frac{RMS[\Delta \theta]_{t-1,i}}{RMS[g]_{t,i}} \, g_{t,i}
$$
ハイパーパラメータ$${\eta}$$が必要なくなりました。
RMSprop
RMSprop(Root Mean Square Propagation)はジェフリー・ヒントンによって2012年に行われたCourseraのオンラインコースの中で提案されたもので正式に論文が発表されたわけではありません。しかし、よく使われるようになりPyTorchやTensorFlowなど多くのライブラリでサポートされています。
RMSpropはAdaDeltaと同じ頃に独立に発案されました。目的はAdaGradの学習率が消失していく問題を解決することで、AdaDeltaの最初の変更点と同様の変更をAdaGradに加えたものです。
$$
E[g^2]_{t,i} = \gamma E[g^2]_{t-1,i} + (1 - \gamma)g^2_{t,i}
$$
$$
\theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{E[g^2]_{t,i} + \epsilon}} \, g_{t,i}
$$
ジェフリー・ヒントンは$${\gamma}$$に0.9を使うことを提案しました。
ADAM
ADAM(Adaptive Moment Estimation)は2015年にICLRでDurk Kingmaらによって発表されました。
AdaDeltaやRMSpropのように勾配の2乗の指数移動平均を使います。それに加えて勾配の指数移動平均も使います。
$$
m_{t,i} = \beta_1 \, m_{t-1,i} + (1 - \beta_1) g_{t,i}
$$
$$
v_{t,i} = \beta_2 v_{t_1, i} + (1 - \beta_2) g^2_{t,i}
$$
$${\beta_1}$$は0.9、$${\beta_2}$$は0.999がよく使われます。
ただし、$${m_{t,i}}$$と$${v_{t,i}}$$を0に初期化するとステップ数がすくない間は0に近い値になりがちなので次の修正を加えます。
$$
\hat{m}_t = \frac{m_t}{1 - \beta_1^t}
$$
$$
\hat{v}_t = \frac{v_t}{1 - \beta_2^t}
$$
この修正はステップが進むにつれ小さくなります。よって、最初の方で値が0に近くなりがちな時だけ修正がかかるようになっています。
まとめると、パラメータの更新式は以下になります。
$$
\theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{\hat{v}_{t,i}} + \epsilon} \, \hat{m}_{t,i}
$$
AdaBound
AdaBoundはAdaGrad、RMSprop、ADAMなどに共通する問題点を解決するために提案されました。その問題は学習率が不安定になりがちで上手く収束しないことです。学習初期ではADAMは学習が速いので、学習後半からはSGDに収束していく仕組みとして、学習率の上限と下限を動的に加えることになりました。2019年に発表されています。
Adamにおける$${\frac{\eta}{\sqrt{\hat{v}_{t,i}} + \epsilon}}$$に相当する部分を上限を無限大、下限を0から始めて徐々に$${\eta}$$に収束するようにします。
参照:Adaptive Gradient Methods with Dynamic Bound of Learning Rate
4.9. AMSGrad
AMSGradはRMSprop、ADAM、AdaDeltaなどに共通する収束しない問題を解決するために提案されました。この問題は学習率が小さくなっていかないことにあるので勾配の2乗の指数移動平均の最大値を使うことで軽減できると考えられました。
$$
\begin{align*}
m_{t,i} &= \beta_1 m_{t-1,i} + (1 - \beta_1) g_{t,i} \\
v_{t,i} &= \beta_2 v_{t-1,i} + (1 - \beta_2) g^2_{t,i} \\
\hat{v}_{t,i} &= \max(\hat{v}_{t-1,i}, v_{t,i}) \\
\theta_{t+1,i} &= \theta_{t,i} - \frac{\eta}{\sqrt{\hat{v}_{t,i}} + \epsilon} \, \hat{m}_{t,i}
\end{align*}
$$
参照:On the Convergence of Adam and Beyond
4.10. AMSBound
AMSBoundはAdaBoundと同様のアイデアをAMSGradに適応したものです。徐々にSGDへと収束していきます。
参照:Adaptive Gradient Methods with Dynamic Bound of Learning Rate
この記事が気に入ったらサポートをしてみませんか?
