円周の長さが 8 となる謎を知る

第１節　はじめに

　平面 R² に原点と ( x , y ) に端点を持つ線分が一つあります．

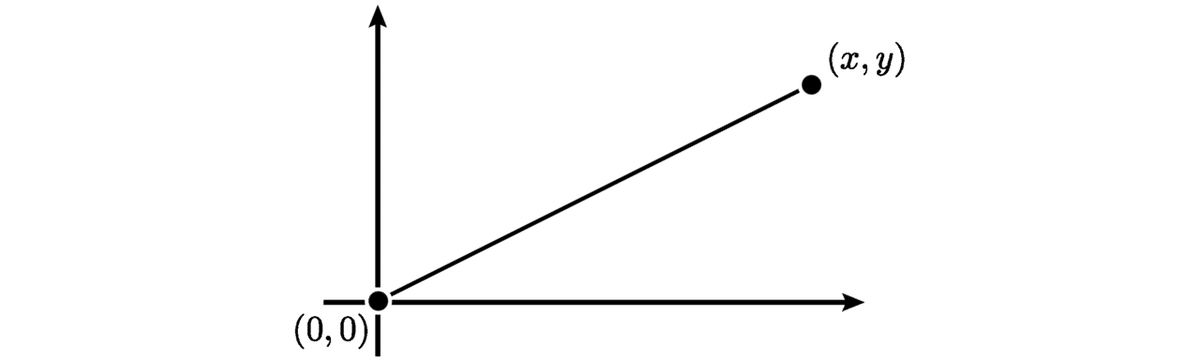
この線分の長さは【明らかに】x + y です．このことは幾何的な直観から簡単に示すことができます．まず，この線分の長さは下図の直角三角形の斜辺の長さです．

　この斜辺の長さが x + y であることを示せばよいのです．いまこの直角三角形の底辺と高さの和は x + y です．そこで直角部分を次のように変形させてみます．

　折れ線部分の長さは依然 x + y のままです．さらにこの折れ線を次のように変形させます．

　この折れ線の長さも x + y のままです．この折れ線の変形操作をどんどん続けていきます．

　この折れ線は長さ x + y を常に保ったまま，斜辺にどんどん近づいていき，やがて斜辺に収束していきます．このことから斜辺の長さは明らかに x + y になるというわけです．

　しかし…残念なことに，斜辺の長さを √(x²+y²) だと言って聞かない者たちがいます．それはわたしたちです．

　わたしたちは，線分の長さが x + y になるはずがないことを知っています．なぜかはわかりませんが，数学に頼らずともそれを知っています．そしていまの議論のどこかに間違いがあることにも気づいています．

　今回は数式に頼ることで，その間違いを見つけていきましょう．

第２節　曲線

　平面 R² 上の曲線とは，一つの実パラメーター t と， t を変数とする微分可能関数 x ( t ) , y ( t ) によって

と書き表せるものとします( I は R 上の区間または R 自身)．

　素朴に言えば曲線とは，一つの実数パラメーターによって表すことのできる【滑らかにつながった線】のことです．例えば微分可能関数 f(x) に対して y=f(x) のグラフは

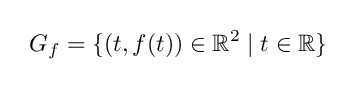
と書くことができるのでこれは曲線です．

　xy - 直交座標において， y = f ( x ) のグラフとして実現できない曲線としては，

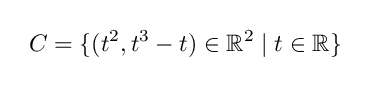
などがあります．

また，原点を中心とする半径 1 の円は

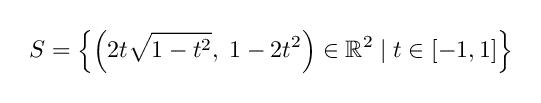
のように書けますが，これも直交座標系において関数のグラフとしては実現できない曲線の例です．

曲線

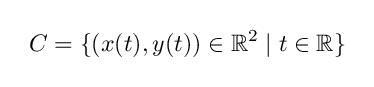
に対して， C ( t ) と書いたら，これは平面上の点  ( x ( t ) , y ( t ) ) を表すこととします．(注意：曲線は単に R² 上の部分集合ではなく，どのような微分可能関数によって表されているかという情報も含めてそう呼ばれることが多いです．あるいは R から R² への連続関数そのものを曲線と呼ぶことも分野によってはあります．）

第３節　曲線の弧長

　曲線の長さのことを【弧長】と呼ぶことにします．いま曲線 C が

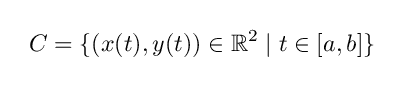
と表されていたとしましょう．このとき， C の弧長はどのように計算すればよいでしょうか．

　今回はすこし厳密さを緩めて素朴に説明しましょう．曲線 C は細かく分割すると，各パーツは直線に近いものになっています．いまこの微小パーツを直線とみなすことにしましょう．

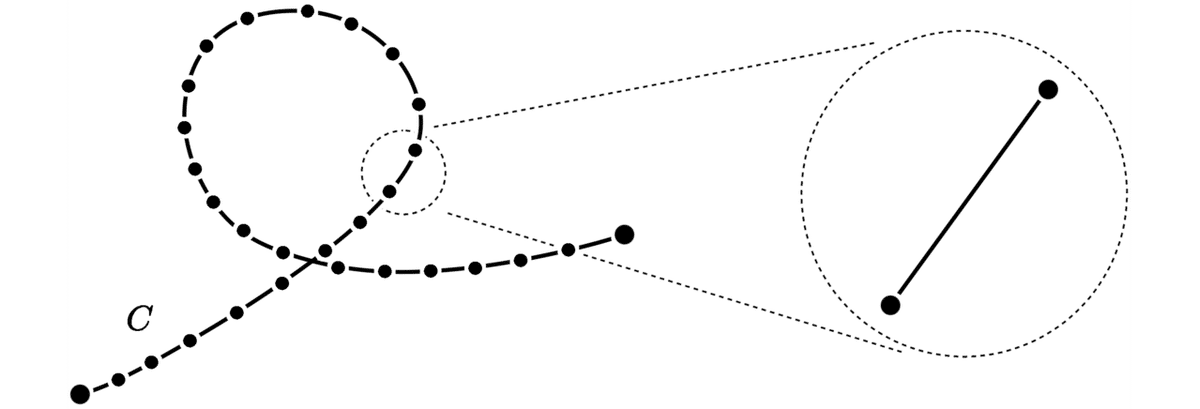
　一つの微小パーツの端点を C ( t ) , C ( t + dt )  とします．ここで dt は非常に微小な実数値を表すものといまはしておきます． C ( t ) と C ( t + dt ) の間の距離を計算するためには， C ( t + dt ) と C ( t )  の間の x 方向の変化分 dx と y 方向の変化分 dy を計算する必要があります．

　C ( t + dt ) = ( x ( t + dt ) , y ( t + dt ) ) ですが．一般に微分可能関数  f ( t ) において，  f ( t + dt ) は

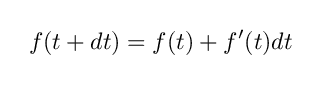
と計算することができます．

　f ' ( t ) というのは f の点 t での1次の変化率を表しているものであり，したがってこの式は， t が dt だけ変化すれば， f ( t ) は  f ' ( t ) dt だけ変化することを表しています．(※注意：2次，3次の変化率も考慮しなければならないように思えますが， dt は非常に微小な数としているため無視しています． dt などの記号は厳密には，関数の1次の部分だけを取り出すものとして定義されます．いまは弧長に焦点を当てたいので，この辺の話は割愛し， dx や dt などの記号を素朴に使っていきます．)

　これを  C ( t + dt ) = ( x ( t + dt ) , y ( t + dt ) ) に適用してみると，

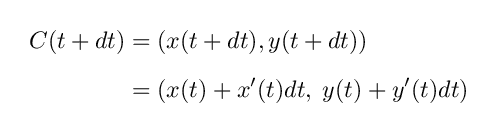
となります．したがって C ( t ) と C ( t + dt ) の間の x 方向， y 方向の変化分 dx , dy はそれぞれ

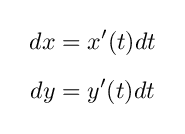
と計算され， C ( t ) と C ( t + dt ) の間の距離は三平方の定理により

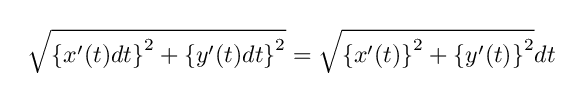
となります．

これによって， C を細分したときの，点 t における微小直線の長さは

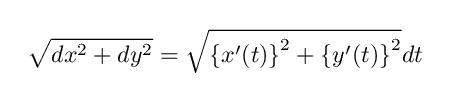
となることがわかります．

　この微小直線の長さを【微小弧長】と呼ぶことにします． C の全体の弧長はこの微小弧長を t = a から t = b まで積分によって足し合わせたものと定義することができます．

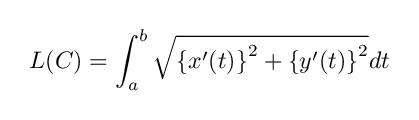
試しに，単位円 S の周長を求めてみましょう．そのために先ほどの円のパラメータ表示

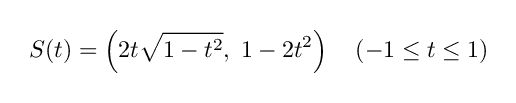
を使います．まず

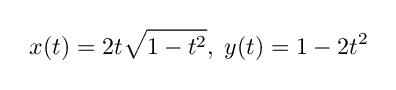
ですから，これらを微分すると

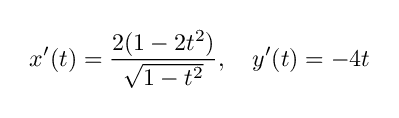
となります．したがって S の微小弧長の式は

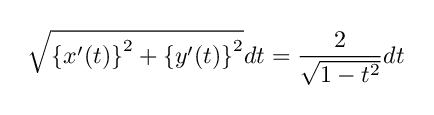
となります．この微小弧長を -1 ≦ t ≦ 1 の範囲で積分によって足し合わせていけば，単位円の周長は

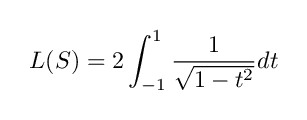
と計算できます．右辺の積分はこれ以上簡単にすることはできません（円周の長さを求めようとしている問題で，円周の長さから定義されるものを使うことはできません．このような問題で例えば cos , sin , π などを即座に使いたい場合，これらの定義が円周を使わずになされていることが必要になります）．そこでこの積分の値の半分を π と定義します．つまり

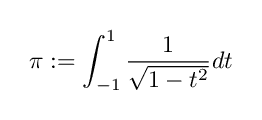
です．この π を【円周率】と呼びます．この記号を使うと

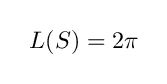
と書くことができます．

第４節　円周の長さは 8 であるか

　曲線の弧長を定義し，単位円の周長が

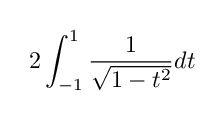
であることがわかりましたが，一方で幾何学的に単位円の周長が 8 であることを示すことができます．

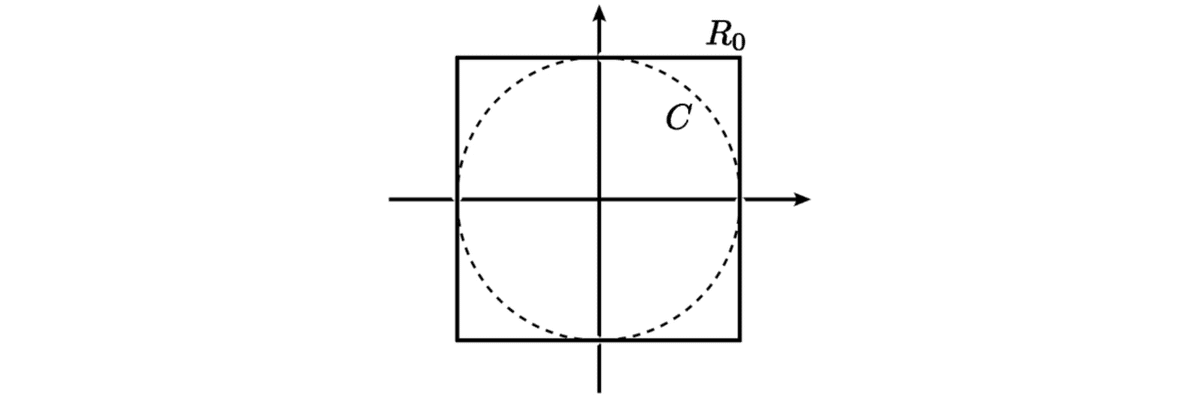
　まず，単位円を次のように囲う正方形を R₀ とします．この正方形の周長は 8 です．

つまり

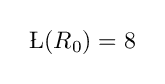
です．

　次に正方形 R₀ の4つのかどを，円にぶつかるように引っ込め，これを R₁ とします．この R₁ の周長も変わらず L ( R₁ ) = 8 になっています．

　さらに同じようにして R₁ の出っ張っている部分を引っ込めて R₂ を作り， R₂ の出っ張っている部分を引っ込めて R₃ を作り...という操作をどんどん続けて Rn を作っていきます．

これら Rn の周の長さはすべて 8 になっていることが確認できるはずです．なぜなら，かどを引っ込めるという操作は周の長さに影響を与えないからです．

　構成の仕方を見てわかるように， Rn は単位円 C に限りなく近づいていきます．つまり

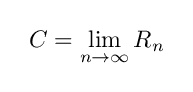
です．なおかつ， Rn の周長は常に 8 なので，その極限である単位円の周長も 8 になってしまいます．よって単位円 C の周長は

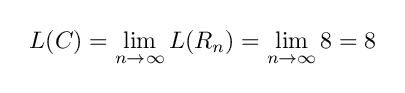
となります．この議論には一見おかしいところはないように見えますが，本当は

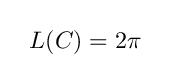
にならなければいけないはずです．では π = 4 なのでしょうか？　当然違います． π は積分値を数値計算すれば 3.1415... です．さきほどの論述のどこかにおかしい部分があることになります．探してみましょう．

第５節　lim[n→∞] Rn = C は正しいか？　図形の収束とは何か？

　まず以上の論述において，数学的にあいまいな部分を考えてみましょう．それはRn が単位円 C に収束するとした

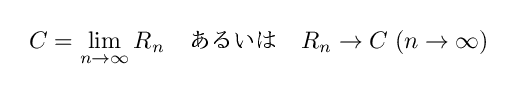
という部分です．

　実は現状，この式は正しいとも間違いとも言えない状況になっています．なぜなら【図形の列がある図形に収束する】とはどういうことかがまだ定義されていないからです．つまり C = lim[n→∞] Rn という式には，まだ意味がないことになります．

　人間の手によって描かれた図表というものは，論理式などによる定義がなければ，あくまで人間の理解の手助けをするための補助的なレプリカに過ぎません．図形が図形に収束するという概念を定義したい場合も，図表のみで論述を進めるのではなく，しっかりと数式で表現されたものに従わなくてはならないのです． Rn→ C (n→∞) が正しいかどうかはその後で判断されることになります．

　では，図形の収束をどのように定義すればよいのでしょうか？

　それを考える取っ掛かりとして，まずは【点の収束】を思い出してみましょう．そもそも点の収束はどのように定義されていたでしょうか．直接的な収束の定義としては距離を使ったものがあります．

　いま，平面 R² 上の2点 a , b の間の距離を d ( a , b ) と表すことにします．すなわち a = ( a₁ , a₂ ) , b = ( b₁ , b₂ ) とすると

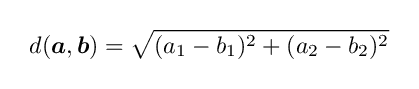
です．これを使うと，点 x_n ∈ R² が a ∈ R² に収束するということを【 d ( x_n , a ) が 0 に限りなく近づくこと】と言い換えることができます．

さらに， 0 に限りなく近づくという文言は， ε - N 論法というものによって厳密に数学的な意味付けを行うことができます．

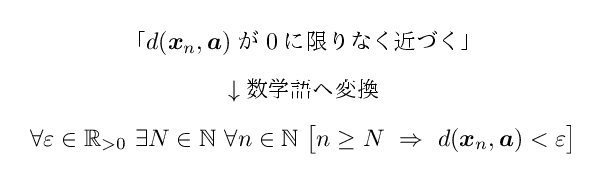
　論理式は複雑なものですが，今回は論理式自体は重要ではありません．重要なのは，収束という概念を定義するためには距離の概念が必要であるということです． xn が a に限りなく近づくということを ε - N 論法を使って定義するためには，【距離】というものは必要不可欠です．いまで言うところの d ( x_n , a )というやつです．逆に言えば，平面上に点と点の間の離れ具合を数値として表す規則が決まっていれば，それを収束の定義に使うこともできます．

　これは平面上の点に限った話ではありません．点とは限らない数学的な対象に，いまのような形で収束という概念を定義したければ，その対象に対して【距離】というものを定めればよいのです．

　図形の収束の話に戻りましょう．図形 An が図形 B に収束すると言ったことを論じるためには，2つの図形の間の距離というものを決めなくてはいけません．例えば，下図の2つの図形の間の距離は◯◯である，と言った具合に，2つの図形の間に【ある非負の実数値を割り当てる規則】を定める必要があるのです．

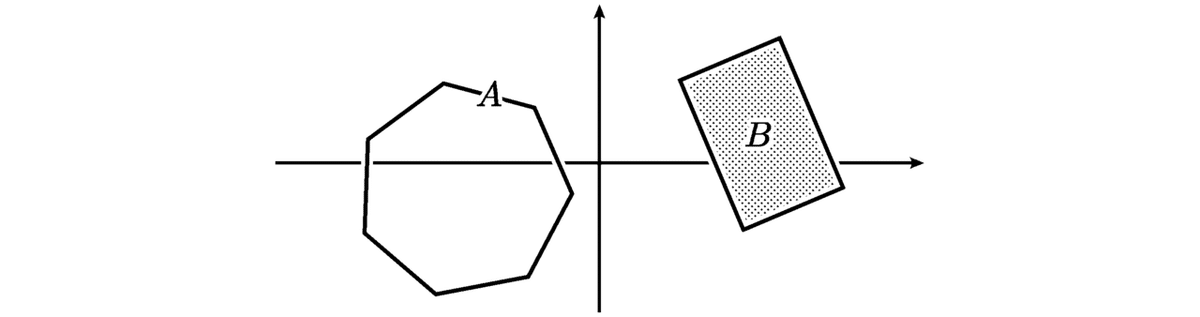
 A と B の間の距離はいくつか？

　問題はどのようにして2つの図形の間の距離を定めるかですが，最初に思いつく方法として，2つの図形の重心の間の長さを測って，それを図形間の距離と定める方法でしょう．

　【距離】という言葉をそのまま解釈すると自然ですが，重心の間の距離は図形の位置関係しか反映しないものになっています．例えば下図にある2つの図形の重心間の距離は 0 になっています．

　つまり重心位置で測る距離では，形が全く違うのに限りなく近いといった状況が発生してしまいます．図形の収束を論じる場合は，2つの図形の形と位置の両方が近いときにのみ小さくなるような距離を考えなければいけません．

　そのような距離の定義は単純にはいきませんが，形情報まで反映した距離のひとつに【ハウスドルフ距離】というものがあります．それが平面 R² 上の図形に対してどのように定まるのかを説明してみましょう．

　まず正の実数 ε に対して，図形 A の ε -近傍 A_ε というものを定義します．これは図形 A のフチ（境界）から ε までの近所の部分を指します．

　A_ε を数式で書くと次のように書くことができます．

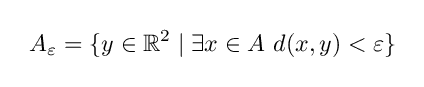
　ちょっとややこしいですが，ここでの d ( x , y ) というのは点と点の間の距離を表すものであって，いま定義しようとしているのは図形と図形の間の距離です．どちらも同じ【距離】という言葉を使うとまずいので，点の距離のことは【ユークリッド距離】，いまから定義しようとしている図形間の距　離は【ハウスドルフ距離】と言いわけていきます．

　さて， ε -近傍というものを定義したことによって，ハウスドルフ距離を定義できるようになります． A と B のハウスドルフ距離 d_H ( A , B ) は，お互いがどれくらいの近傍にあるのかを数値化したもので，

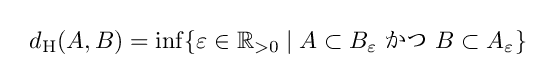
と定義されます．

ハウスドルフ距離 d_H ( A , B ) = ε

　この定義式の右辺がどのようなものかを説明してみます． inf というのは【下限】を意味する数学記号です．右辺は， A ⊂ Bε かつ B ⊂ Aε を満たすような最小限の実数 ε を取ることを意味しています．つまり，お互いの ε -近傍がお互いを含むような状況を作り出す最小限の実数値を2つの図形のハウスドルフ距離と定義するわけです．

　なにか例を持ってきましょう．例えば下図にあるような2つの図形のハウスドルフ距離を考えてみます．

　この場合， ε > 3 であれば以下が成り立ちます．

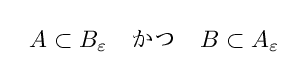
しかし ε ≦ 3だと成り立っていません．よって互いが互いを覆うために必要な近傍は 3 -近傍ということになり，

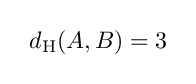
となります．

　次に，正方形と単位円の例を考えてみましょう．

さきほどと同様にして考えると， C と R の √2 - 1 より大きい近傍はお互いを覆っており，それより小さい近傍を考えると

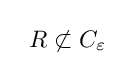
となることが確かめられます．

　したがって，互いが互いを覆うことのできる最小限の近傍は ( √2 - 1 ) - 近傍であり，

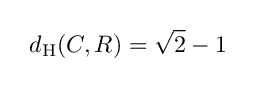
となることがわかります．

　このハウスドルフ距離は，図形同士の形の近さをしっかりと数値化しています．これによって図形の【形の収束】をハウスドルフ距離が 0 に限りなく近づいていくこととして論じることができるようになるのです．

　ここで，単位円をギザギザな線で近似していった最初の話に戻りましょう．単位円は C ，ギザギザな線は R_n という記号で書かれていました．ハウスドルフ距離を使うと，次のことが言えます．

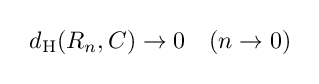
つまり Rn と C の間のハウスドルフ距離は限りなく 0 に近づいていきます．これを論理式でしっかりと書くと

という（例によって厄介な）感じになります．ここで重要なのは，図形の収束を d_H ( Rn , C ) を使うことによって数式に落とし込むことができたという点です．

　d_H ( Rn , C ) は 0 に限りなく近づいていくため， Rn は C に（ハウスドルフ距離の意味で）収束するということが従います．この事実を， Rn は C へハウスドルフ収束すると言い，

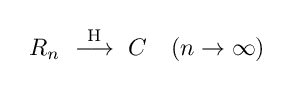
と書いたりします．

Rn が C へハウスドルフ収束する様子

　したがって，ハウスドルフ収束の意味において， R_n が C に収束するということは数学的に正しい事実ということになります．

　では， C の弧長が 8 であるという結論を出してしまった論述のどこに間違いがあったのでしょうか．

第６節　lim[n→∞] L ( Rn ) = L ( C ) は正しいか？

　結論から言えば，誤りなのはこの部分です．

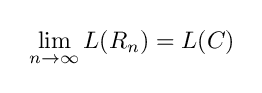
　この式は R_n の周長の極限が C の周長に一致するということを述べていますが，一般には曲線の列 A_n が曲線 B にハウスドルフ収束するとしても， A_n の周長の極限が B の周長に一致するとは限りません．

　今回のように，円周をギザギザで近似する例は見た目で正しいように感じてしまいますが，以下のような極端な例を挙げることもできます．

A_n は図形的には線分 B にハウスドルフ収束していきます．すなわち

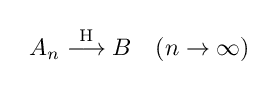
です． A_n のでこぼこの数は4倍ずつ増えており，その弧長は L(An)=2^n+2^(1-n)+1 と計算することができます．その極限は

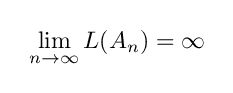
となります．明らかに A_n の弧長は B の弧長である 1 という値には近づきません．図形がハウスドルフ収束するからといって，弧長も極限の図形のものに収束するとは限らないということです．

　しかし，ここで疑問が生じると思います．図形の極限を考える際，途中のでこぼこの情報はどこに消えてしまうのだろうかと．見たとおり A_n は細かいでこぼこがたくさん存在するような曲線です．しかし極限である B にはその情報は一切なくなっています．それによってハウスドルフ収束と弧長の収束の間に，整合性がなくなっています．その理由を感覚的に解釈してみましょう．

　図形の極限と長さの極限が一致しない根本的な原因は，それぞれの収束では，考えている【次元】が違うことが挙げられます．どういうことか説明してみます．

　まず，曲線の弧長というものは

のように，【微小な1次元の長さ】によって決定されるものです．曲線全体の弧長はこれを積分することによって得られています.つまり弧長の極限というのは，図形を1次元的な視点からみた極限であると言えます．

　それに対して図形の極限というものは【 ε -近傍】という2次元的な概念によって得られるものです．図形として2つのものが近いということを認識するとき，必ずその図形の近傍というものを暗に考えています．たとえ図形が1次元的なものであってもそうです．

　R_n や C は1次元的なものですが，図形として収束するということを考えるときに，必ずその ε -近傍を考えています． R_n の【でこぼこ情報】は， ε -近傍という2次元的なものに吸収されて消えてしまっていると解釈することができます．

　2次元的な収束概念に対して，1次元の長さの極限が整合性を持たないのは，ある意味で当然と言えるかもしれません．それが L(R_n) の極限が L(C) に一致しない感覚的な理由ということになります．

　ハウスドルフ収束が1次元的なものではないということを意識する例があります．それは以下に示すものです．

　各 A_n は1次元の曲線ですが，極限の B は2次元の面になっています．このことからも平面図形の極限というものは本質的には2次元的なものであるということがわかります．

　ハウスドルフ収束の概念は3次元空間（あるいはもっと高次元の空間や一般の距離空間）の中の図形に対しても定義されるものであり，3次元空間内での図形の収束概念は3次元的なものになります．

1次元の図形が3次元の円柱に収束する

　このように【図形の収束】と【弧長の収束】の間には直接の関係性がないことが分かります．

参考文献および関連するページ

Christina Sormani "How Riemannian Manifolds Converge Metric and Differential Geometry", pp 91-117

ハウスドルフ距離(Wikipedia)

グロモフーハウスドルフ収束 (Wikipedia)

コメント

　曲線を直角折れ線近似しても，それが弧長とは一致しない感覚的な理由を探していましたが，以上のようなことだと私は考えました．このことに関しては，これとは違った意見があるかもしれません．測度論などの観点から見るとまた違った見方が生じてくるかもしれません．

　とにかく【図として描く】幾何学にはこういった危うさがいくつも隠れているようです．数学的にこれを追求してみるのもまた面白いものです．

　次回は【弧長】と密接な関係にある【距離】の話をし，それにまつわる三角関数の話をしてみたいと思います．