電気のおはなしその50・交流の性質(2)sin・cosと円の関係
電気の勉強というと、難しい数式がいっぱい出てきて、それで嫌になっちゃう…という話を耳にします。でも、これまでに書いてきた内容の大部分を占める直流回路に関しては、せいぜい抵抗が複雑に組み合わせられた回路でちょっと複雑な分数の計算が出てくることがある…という程度で、難しいといっても別にたかが知れたレベルのお話でした。
しかし、交流の電気になると、三角関数が出てきたり虚数が出てきたりして、急に難しい話になってしまうイメージがあるかと思います。特に、三角関数のsinだのcosだのが出てくると嫌~!ってなっちゃうことが多いかと思うんですよね。どこかの首長だかが「三角関数なんて勉強しても何の役にも立たない!」と言い放っただとか、それに対して「いや、三角関数は山の高さを求めるために使えるよ!」という声が上がり「山の高さを求めることが人生で何回あるんだよ」なんて突っ込みが入ったりとカオスな様相を呈するわけですが、今回は三角関数が出現した経緯、円と三角関数の関係、三角関数とベクトル、位相差と虚数…という流れで、"何のために暗記しているか分からない難しい数学"からの脱却を図っていきたいと思う次第でございます。
閑話休題。前回の宿題。
円は一周360度ですが、何故切りのいい100度みたいな値ではなく、中途半端な360度という角度になったのでしょうか?
答えは、「一年がほぼ360日だから」です。
地球は太陽の周りを回っています。日が最も短い冬をスタートとすれば、やがて春が来て、夏が来て、秋が来て、そしてまた冬に戻ります。
はるか昔、紀元前の頃の人類は、春夏秋冬の周期が数百日で繰り返すことに気が付きました。また、地球上から見える星の位置も周期的に元に戻ることに気が付いたのです。そこで、石板かパピルスか分かりませんが、一日一日を記録し始めたのですね。
すると、約360日で一周して元に戻ることや、約90日周期で春・夏・秋・冬と移ろっていくことが分かりました。夜に見える星の位置も、北極星を中心として円を描いてやはり360日程度で元の位置に戻りました。
そうなると、図を描いて天体の運動と季節の移ろいなどの関係を調べたくなります。っていうか、歴史上そうなりました。
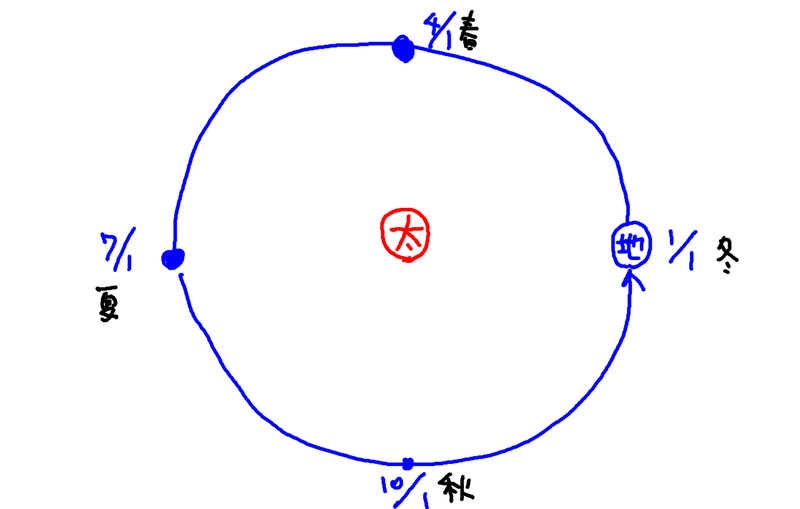
で、要するに角度1度というのは、一日に地球が移動する角度なんです。
さて、まずは春・夏・秋・冬の地球の位置。これは、それぞれ直角の位置関係ですから、これは分かりやすいでしょう。
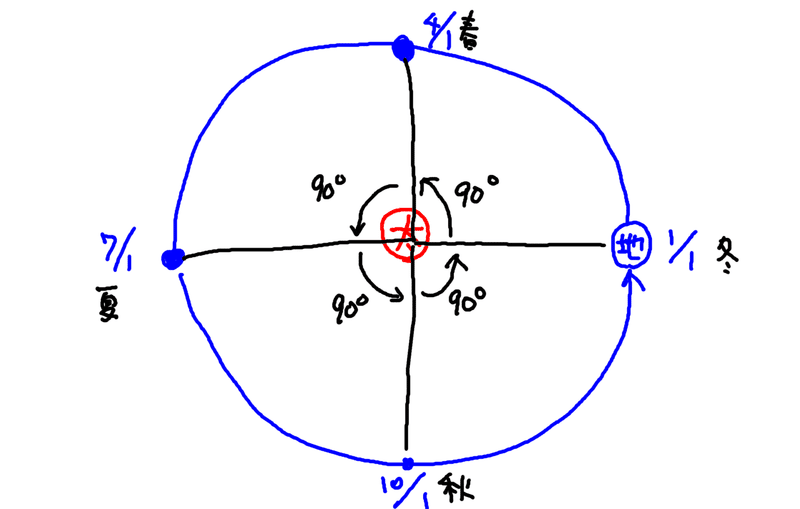
ここまで分かってくると、次に知りたいのは、任意の日付のときに地球が一体どの辺の位置にあるか、ということになります。
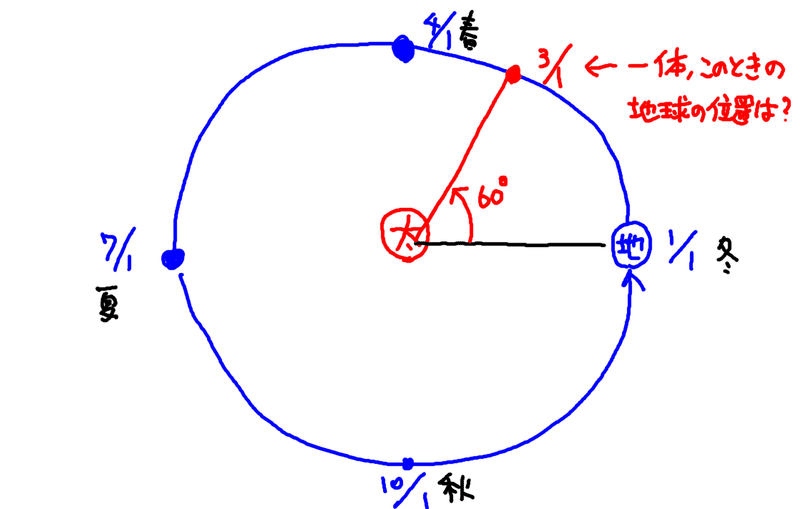
例えばこのように、スタートから60日目の地球の位置は一体どこなんだろう??という場合ですね。
任意の日付の時に地球が一体どこにあるかを知ることができれば、例えば海上を航海していても、星空を見上げて観測すれば今が何月何日なのか求めることができるなど、様々な応用ができることになります。
そこで、スタートからの日付(=角度)に対する、円軌道上にある地球の位置を求める研究が進みました。
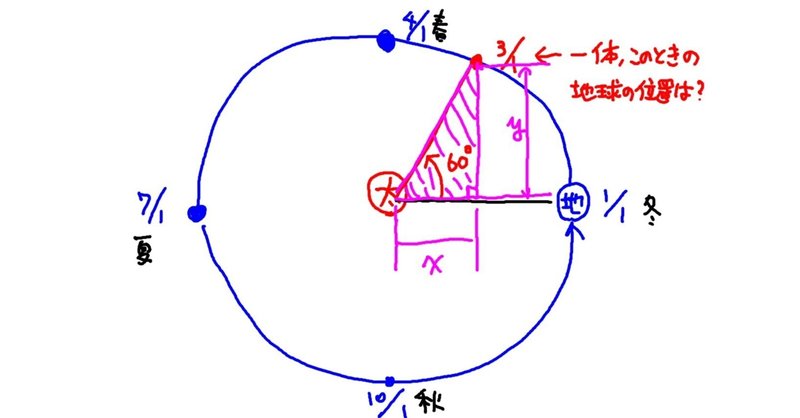
ここで注目されたのは、太陽と地球との距離は年間を通して変わらない、という点です。それに着目して、下図のように直角三角形を描き、このときの角度と辺の長さとの関係を調べていけば任意の日付の地球の位置が分かることになります。
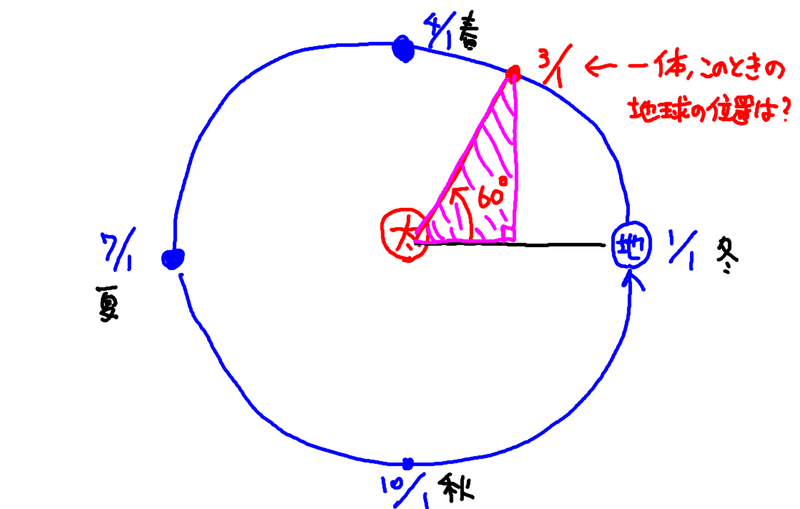
というわけで、ここでようやく直角三角形が出てきました。
三角関数が求めたいものは、
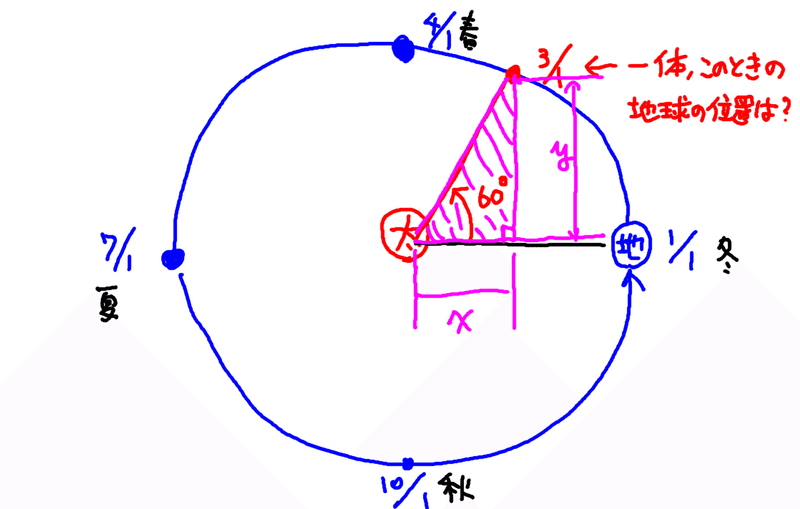
この図のように、ある角度と直角を持った三角形について、斜辺(=これが、太陽と地球との距離に該当します)の長さに対するxとyの長さです。
前回、次のような図を描きましたが、

この三角形において、斜辺の長さAが太陽と地球の距離に該当しますから、この長さを「1」と置いてみると、
sinθ=C÷A=C÷1=C
cosθ=B÷A=B÷1=B
となり、ある角度θに対するsinやcosの値がそのまま地球の位置のx座標とy座標に対応してしまうことが分かるんですね。
今回、sinのグラフの話まで入るかな?と思いましたが、ここまででもう1800文字書いているので、グラフなどについては次回にしますね。
三角関数はいきなり出てきたわけじゃなくて、太陽と地球の位置関係から生まれたもの。だから円の角度は、一年間の日数とおぼ同じ360度。
はい。覚えましたねー。
以上。
この記事が気に入ったらサポートをしてみませんか?
