最適化問題:単体法アルゴリズムの理論
この記事は データ構造とアルゴリズム Advent Calendar 2019 6日目の記事です。
こんにちは、こんばんは。kaneshin です。現在は株式会社エウレカでCTOをしてエンジニアリングをメインに仕事をしていますが、学生の頃は最適化理論における非線形計画法を研究していました。そのころから来年で10年が経過しますが、最近は iOS アプリ開発で Auto Layout として、Android アプリ開発では Constraint Layout で最適化問題の線形計画法の解法の一つ『単体法』 (Simplex Method) が使われているので嬉しくなります。
参考:USING THE SIMPLEX METHOD FOR SOLVING LAYOUT
CONSTRAINTS IN SCIENTIFIC DIAGRAMS
最適化問題とは
最適化問題とは、自然科学や工学などの領域において発生する基本的な問題の一つです。
与えられた条件のもとで何らかの関数を最小化もしくは最大化するような問題で、与えられる条件や変数の数が有限個扱うことを数理計画問題と総称し、今までに理論的な研究や数値解法の研究がなされてきました。
最適化問題に対してデータ的アプローチの研究も盛んになされており、最適化問題への機械学習や深層学習の応用が日々研究されています。
最適化問題や、その上位概念のOR (Operations Research) についてより一層詳細を知りたい場合、上にあるスライドを最初のページから参照してお読みください。
単体法とは - シンプレックス法 (Simplex Method)
線形計画問題の解法の一つに George B. Dantzig 教授によって提案された単体法(シンプレックス法)という有限回で最適解に到達するということが保証されたアルゴリズムが有名です。有限回で最適解に到達するのが保証されている理由は、最適解が端点に現れることを利用しているためです。

この単体法は非常に有効な線形計画法の数値解法として広く使われているため、非常に有用なのですが問題点も存在します。単体法は有限回で最適解に到達することが保証されているのですが、制約式の本数が増えることによって計算時間が指数関数的に膨大になる可能性があります。
単体法のアルゴリズムの原理
単体法で線形計画問題を解くアルゴリズムの説明ではなく、その裏側にある原理について解説します。それを知るには単体法の原理の前に、線形計画法における基本定理を知ることが大事になります。
線形計画法の基本定理
線形計画問題の標準形 が与えられたとき、下記の (1) と (2) が成り立つ
(1) 実行可能解が存在するならば、実行可能基底解が存在する
(2) 最適解が存在するならば、実行可能基底解の中に最適解が存在する
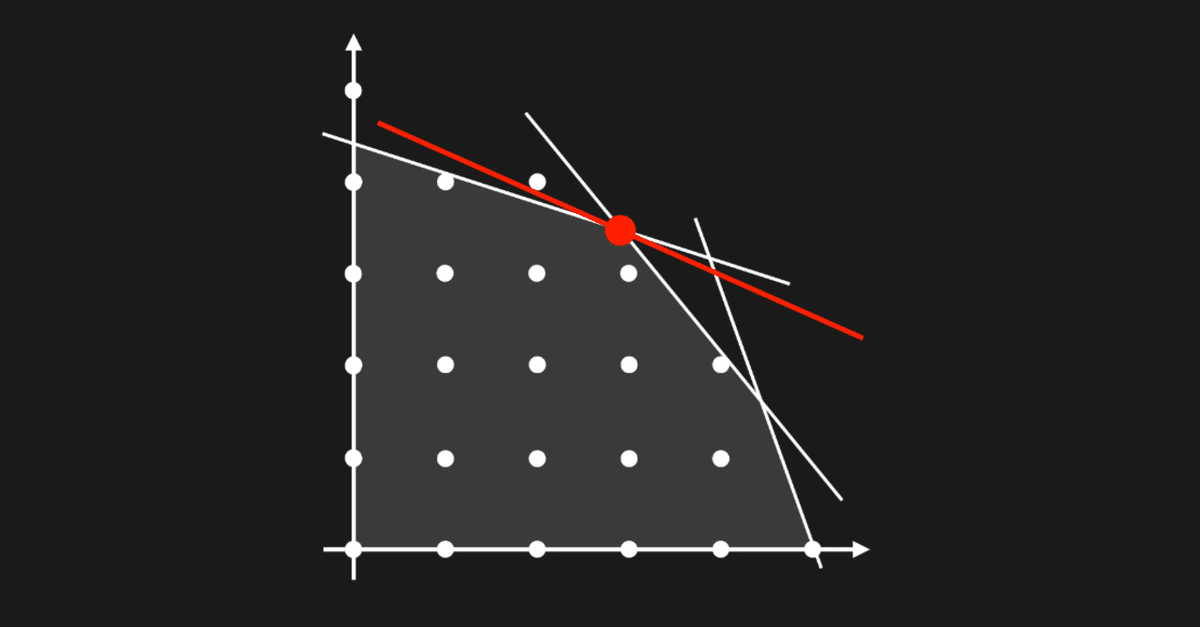
実行可能解とは制約条件を満たす点で、その点の集合を実行可能領域と呼びます。上にあるグラフでいえば、薄い白いところ(軸と線形式に囲まれた領域)が実行可能領域となります。そして、実行可能基底解とは、それぞれのグラフもしくは軸の交わる端点になります。

この画像の矢印のところが実行可能基底解になります。ただ、グレーで塗りつぶされた実行可能領域に隣接していない実行可能基底解を退化しているといい、最適解には成り得ません。分別するために、隣接する実行可能基底解のことを非退化実行可能基底解とも呼びます。
単体法では、目的関数値を下げながら(上げながら)実行可能領域の隣り合う端点(つまり、隣り合う非退化実行可能基底解)へ移動しながら最終的に最適解に到達していきます。

実際のところ、この線形計画法の基本定理を知ってしまえば何ということはないと思いますが、単体法では基底変数を選んでから単体法としての実行可能基底形式といわれる正準系に標準形を変形させて解く必要があります。
変形させた式は、それぞれ基底変数と非基底変数に対応する行列と変数に分けられ、それぞれの部分がアルゴリズムの各ステップで最適性の基準をはかる指標にしたり、実行可能基底形式をアップデートすることになります。
単体法のアルゴリズムのステップについては、Wikipedia や Google 検索で論文を探してみてください。
おわりに
最適化問題は自然科学や工学として応用できるところが多いですし、まだまだ研究され続けている分野です。これを機に興味を持って勉強をしていただけたら嬉しいです。
あと、数式が必要な記事を note で書くのは非常に難しいですね。はてなブログに書けばよかったかなと思いつつ、はてなブログでも書きにくいんですよね。
さいごに、途中で記事を全消ししてしまって復元できなく、泣く泣く書き直しました。
この記事が気に入ったらサポートをしてみませんか?
