ラウンドワンのポテト

昨日のことである。大学の友達が久々に大阪に戻ってくるということで、飲み会をしたのであった。９０分の食べ放題のお店だったので、時間があまってしまったので、久々に学生の頃のようにビリヤードかダーツでもしようかといことで、駅前のラウンドワンに行くことにした。ダースが混んでいたので、ビリヤードを始めたのである。

今風で、ビリヤード台には、情報端末がおかれており、「選べる！マイポテト！組み合わせはなんと10,000通り以上！」なんて文字が躍っている。
『いや、ちょっとまってよ、チャート式じゃないのに、こんな街中で問題が出題されているだなんて！今ちょうど組み合わせの章のところやってるんですよ！』（心の声）
こうなったら、ビリヤードの合間に本当の組み合わせの数を計算したくてうずうずしてしまう。

大丈夫。友達には、最近、高校数学にはまっていることをカミングアウトしているので、変な目で見られることはない。周りからはわからん。

もう計算してくれと言わんばかりにちっちゃいホワイトボードまで用意されている。（本当は、勝ち負けを記録するためだと思われ）

さて、興味深い問題の内容に移ろう。

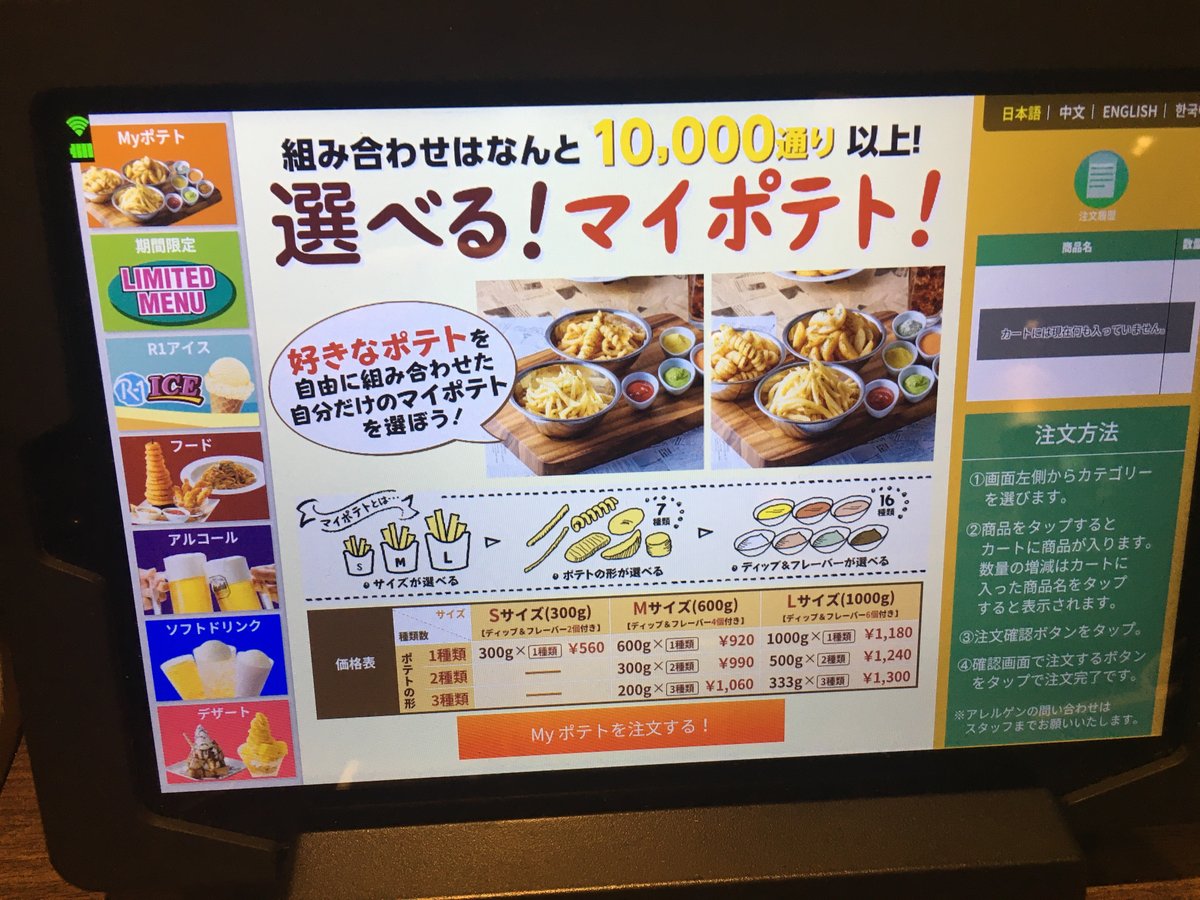
問題を整理しよう。ただ、実際にポテトを頼んでいないので、例外的なルールはよくわからない。あくまで画面で確認できた条件を見てみる。

1. サイズはS M Lの3種類選べる。

2. それぞれのサイズに対し、7種類のポテトの形状を選ぶことができる。ただし、Sサイズは1種類のみ、MとSサイズは、1～3種類選ぶことができる。

3. さらに16種類のディップ＆フレーバーを選ぶことができる。Sサイズの場合は2種類、Mサイズの場合は4種類、Lサイズの場合は6種類である。

条件はわかった。さっそく場合分けをして、組み合わせの数を計算しよう。

Sサイズ - 形状：7種類中1種類 - ディップ＆フレーバー：16種類中2種類

$$
7 \cdot {}_{16} C_2 = 7 \cdot 120 = 840 (通り)
$$

Mサイズ - 形状：7種類中1種類 - ディップ＆フレーバー：16種類中4種類

$$
7 \cdot {}_{16} C_4 = 7 \cdot 1820 (通り)
$$

Mサイズ - 形状：7種類中2種類 - ディップ＆フレーバー：16種類中4種類

$$
{}_7 C_2 \cdot {}_{16} C_4 = 21 \cdot 1820 (通り)
$$

Mサイズ - 形状：7種類中3種類 - ディップ＆フレーバー：16種類中4種類

$$
{}_7 C_3 \cdot {}_{16} C_4 = 35 \cdot 1820 (通り)
$$

つまり、Mサイズすべての場合は、

$$
(7 + 21 + 35) \cdot 1820 = 63 \cdot 1820 = 114,660 (通り)
$$

あれ、もう10,000通り超えてますけど・・。気を取り直して、Lサイズの計算に入る。

Lサイズの形状の組み合わせは、Mサイズと同じなので、

$$
7 + 21 + 35 = 63(通り)
$$

ディップ＆フレーバー：16種類中6種類の組み合わせは

$$
{}_{16} C_6 = 8,008 (通り)
$$

つまり、Lサイズの組み合わせは、積の法則で、

$$
63 \cdot 8008 = 504,504(通り)
$$

和の法則より、Sサイズ、Mサイズ、Lサイズの組み合わせは、

$$
840 + 114660 + 504504 = 620,004 (通り)
$$

はい、はい、お疲れ様。手計算だったので、間違っていたらすまぬが、この功績を余白に書きたくて仕方なく、ホワイトボードに堂々と書いておいた。この後、片づけに来た店員さんは驚愕的な事実に震えただろう。

『過少広告すぎでしょ！！！！！せめて50万通り以上とか言ようよ！絶対途中で計算あきらめたでしょ！！』

すみません。偶然起きたネタ記事でした。

後日談。
娘にこのことを話して、こういうことがあるから数学は役に立つんだよと力説したら、娘からは「役には立ってねーよ」と言われた。