
公開情報からトリガー率を計算する
こんにちは。
チームGlänz(グレンツ)所属のiroと申します。
日々楽しくデュエプレをしています。
よくビートダウンデッキを使うせいか、対戦の際、相手の盾に何枚のトリガーが埋まっているのかを常に気にしています。
デッキタイプでだいたいのトリガー枚数は予想できますので、ゲーム開始時の確率はDMwikiなどを見ればわかります。
では、相手のマナゾーンにトリガーが見えた時はどうでしょうか?
トリガーカードを手打ちされた時は?
つまり、公開情報によって盾にトリガーがある確率が変化するのかどうかということです。
今回、いろいろ計算してみましたので、皆様に共有したいと思います。
結論
結論から述べ、後ほど詳しく証明を行います。
公開情報によって、盾のトリガー期待値は変化し、以下の式で計算できる。
図のように、

公開カード$${n}$$枚中、見えたトリガーが$${s}$$枚のとき、盾のトリガー期待値は、
$${期待値=\frac{5×(デッキのトリガー総数-s)}{40-n}}$$
で求められる。
ここで、トリガー総数-s は非公開トリガーカード(見えていないトリガーカード)、40-nは非公開カードを表しているので、

すなわち、期待値は
$$
\cfrac{5×非公開トリガーカード}{非公開カード}
$$
となる。
例 トリガー8枚のデッキで、20枚中3枚のトリガーが見えた場合
→盾も含めて非公開カード20枚、非公開トリガー5枚となるので、盾のトリガー期待値は5×5/20=1.25枚

また、(盾1枚あたりの)トリガー確率×盾の枚数で期待値を求められることから、以下のことがわかる。
$${トリガー確率×5 = \frac{5×非公開トリガーカード}{非公開カード}}$$
よって、盾1枚あたりのトリガー確率は、
$${トリガー確率 = \frac{非公開トリガーカード}{非公開カード}}$$
例 先ほどの状況(トリガー8枚のデッキで、20枚中3枚のトリガーが見えた→非公開カード20枚、非公開トリガー5枚)の場合
上の式で計算するとトリガー確率は5/20=25%
もともとは40枚中トリガーが8枚であったので、8/40=20%
つまり、公開情報によって盾のトリガー確率が変わるということです。
盾はドローの前に置かれるため、事前に置いたカードの確率が、その後の公開情報により変化するということは、割と直感に反するのではないでしょうか。
また上記の式が、非公開トリガーと非公開カードの商という、非常に簡単な形になっている点も疑い8割驚き2割かと思います。
それでは、以降計算方法と、詳しい証明に移ります。
計算方法
公開情報について、見えているカードn枚中s枚がトリガーであったとします。

① 盾にトリガーが埋まる確率(0枚〜5枚)を求める
デッキのトリガー枚数によって、ゲーム開始時からわかる確率です。
・例えば、トリガーが8枚のデッキでは、
0枚(ノートリ)→30.60%、1枚→43.72%、2枚→21.11%、3枚→4.22%、4枚→0.34%、5枚→0.01% となります。
DMwikiにも載っている値ですが、のちの計算のため、組み合わせの総数を用いて計算しておきます。
② ①のそれぞれの場合で、「n枚中s枚トリガーが見える」という事象が発生する確率を求める
・例えば、トリガー8枚のデッキで、20枚中3枚のトリガーが見えた場合(n=20, s=3)

この時に盾のトリガー枚数で場合分けをして、「20枚中3枚のトリガーが見える」という事象が起こる確率をそれぞれ求めます。
盾にx枚トリガーが埋まっているとすると、初期山札35中、8-x枚がトリガー、35-(8-x)=27+x枚が非トリガーカードになるので、
8-x枚から3枚
27+x枚から17枚
を取り出す組み合わせを考えて、
$${\cfrac{{}_{8-x}C_3 × {}_{27+x}C_{17}}{{}_{35}C_{20}}}$$
を計算することで、確率を求められます。
x=2のとき、この確率は32%ほどになります。これは初期山札35枚中6(=8-2)枚がトリガーのとき、20枚めくって3枚トリガーが見える確率が32%ほどということです。
③ 盾のトリガーが0枚〜5枚それぞれの場合の①と②の確率をかけあわせる
これにより、「盾にトリガーが◯枚」かつ「そのときに山札をめくってn枚中s枚トリガーが見える」確率が計算できます。
④ 各場合の③の計算結果をすべてたしあわせる
これにより、「n枚中s枚トリガーが見える」という事象の確率を計算します。
・下の画像はトリガー8枚のデッキで、n=20、s=3としています。
つまり、このデッキにおいて「20枚中3枚のトリガーが見える」という事象は、③の総和である22.98%の確率で発生するということです。
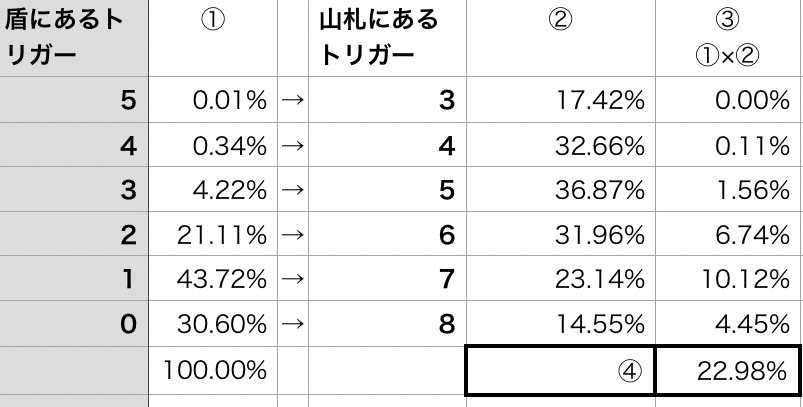
ただ、この確率がどうこうではなく、大切なのは22.98%の内訳です。
⑤ ③/④を計算する
これにより、「n枚中s枚トリガーが見える」という事象が発生したときに、「盾のトリガーが◯枚である」確率(条件付き確率)を求めることができます。

①の列と⑤の列を比べることで、「20枚中3枚トリガーが見える」という事象による、盾のトリガー確率の変化を見ることができます。
例えば2トリする確率は、「20枚中3枚トリガーが見える」という事象が発生したことによって、当初21.11%だったのが、29.35%まで上昇しています。ノートリ率は10%近く下がっています。
極端な話ですが、10000回このデッキを回した時、10000×④22.98%=2298回「20枚中3枚トリガーが見える」という事象が発生します。
③の確率から考えて、そのうち
10000×4.45%=445回はノートリのときで、
10000×10.12%=1012回は1トリのときで、
10000×6.74%=674回は2トリのときで、
…などと考えられ、
ノートリの確率は$${\dfrac{445}{2298} = 19.37\%}$$
1トリの確率は$${\dfrac{1012}{2298} = 44.02\%}$$
2トリの確率は$${\dfrac{674}{2298} = 29.35\%}$$
…などと、⑤の確率が求められるということです。
⑥ ⑤の確率を用いて期待値を求める
1トリの確率×1+2トリの確率×2+……+5トリの確率×5 を計算します。

当初のトリガー期待値は、
トリガー率 $${\frac{8}{40}}$$なので、
$${\frac{8}{40} × 5 = 1.000枚}$$でした。
この変化も、「20枚中3枚トリガーが見える」という事象が発生したことによるものです。
ここまでのことをまとめると、
盾のトリガー数と山札のトリガー数の総和は必ず一定なので、山札をめくっていった公開情報から盾のトリガー率や期待値を計算できるということです。
次に、このことを一般化します。
一般化

このような表計算シートを作成し、公開領域の数をポチポチと上下させながら遊んでいたところ、公開カードの数が5の倍数のとき、見えたトリガー数を変えたときの期待値の変化が非常に規則的になっていることに気がつきました。
具体的には、
公開カードが15枚のとき、見えたトリガー1枚につき期待値が0.2ずつ変化し、公開カードが20枚のとき、見えたトリガー1枚につき期待値が0.25ずつ変化していました。
$${15 → 0.2=\frac{1}{5}}$$
$${20 → 0.25=\frac{1}{4}}$$
ということは…と思い、公開カードを25枚にしてみると、予想通り$${0.33…=\frac{1}{3}}$$ずつ期待値が変化していました。
つまり、公開カードがn枚の時、期待値の変化量は
$${\cfrac{5}{40-n}}$$
となるのではないかと考えました。
実際、この式は
n=15のとき、$${\frac{5}{40-15} = \frac{1}{5}}$$、
n=20のとき、$${\frac{5}{40-20} = \frac{1}{4}}$$となります。
よって、デッキ内のトリガーがすべて見えたとき、期待値は0になることから、トリガー期待値を求める式は、n枚中s枚のトリガーが見えたとき、
$${\cfrac{5}{40-n} ×(総トリガー数 - s)}$$
となるのではないかと予想しました。
これが、このnoteの一番初めに出した式になります。
実際に色々な値で試しましたが、表計算シートで出した⑥の期待値と、この式の計算結果は一致していました。

$${\dfrac{5}{40-10} ×(12-1)=\cfrac{55}{30}=1.833…}$$
次にこのことを証明します。
証明
(読み飛ばして大丈夫です)
トリガー枚数が$${S}$$枚のデッキにおいて、公開カード$${n}$$枚中$${s}$$枚がトリガーであったとする。このとき、盾のトリガー期待値が、
$$
\frac{5×(S-s)}{40-n}
$$
であることを証明する。
① 盾に$${a}$$枚のトリガーがある確率を求める
ただし、$${a=0, 1, 2, …, 5}$$であり、$${a < S}$$であるとする。
盾のカード5枚の選び方を考えます。
・トリガーカードS枚からa枚を選ぶ
→$${{}_SC_a}$$
・非トリガーカード40-S枚から5-a枚を選ぶ
→$${{}_{40-S}C_{5-a}}$$
なので、
$$
\cfrac{{}_sC_a × {}_{40-S}C_{5-a}}{{}_{40}C_5}
$$
となります。
② このとき、公開カードn枚中s枚がトリガーである確率を求める
公開カードn枚の選び方を考えます。
いま、手札を配る前の山札35枚のうち、
・S-a枚がトリガーで、ここからs枚を選び、公開カードとする
→$${{}_{S-a}C_s}$$
・35-(S-a)枚が非トリガーで、ここからn-s枚を選び、公開カードとする
→$${{}_{35-(S-a)}C_{n-s}}$$
なので、
$$
\cfrac{{}_{S-a}C_s × {}_{35-(S-s)}C_{n-s}}{{}_{35}C_n}
$$
となります。
③ ①と②をかけあわせる
$$
\dfrac{{}_sC_a × {}_{40-S}C_{5-a}}{{}_{40}C_5} × \dfrac{{}_{S-a}C_s × {}_{35-(S-s)}C_{n-s}}{{}_{35}C_n}
$$
式が大変なことになっていますが、これを組合せの性質
$$
{}_nC_r = \cfrac{n!}{(n-r)!r!}
$$
を用いて気合いで変形すると、次のようにまとまります。
$$
\dfrac{{}_5C_a × {}_{n}C_{s} × {}_{35-n}C_{S-s-a}}{{}_{40}C_S}
$$
実際この式について、次のようにも考えられます。
図のように、40枚のカード置き場を用意し、そこにS枚のトリガーカードを置いていくことを考えます。

初めの5枚(盾)のなかからa枚を置く場所を選び、そのあとのn枚(公開カード)からs枚を置く場所を選び、35-n枚(山札)から、残りのS-s-a枚を置く場所を選ぶとします。
残りの場所に非トリガーカードが置かれると考えると、この選び方の総数は、盾・公開カード・山札に含まれるトリガーがa枚・s枚・S-s-a枚の配分となるパターンの総数と一致します。よって、この事象の確率は、
$$
\dfrac{{}_5C_a × {}_{n}C_{s} × {}_{35-n}C_{S-s-a}}{{}_{40}C_S}
$$
であると考えられ、先ほどの式の説明がつきます。
④ ③をたしあわせる
和の記号$${\sum}$$を用います。
$$
\sum_{a=0}^{5} \dfrac{{}_5C_a × {}_{n}C_{s} × {}_{35-n}C_{S-s-a}}{{}_{40}C_S}
$$
いま、nとsはaに関係のない値なので、
$$
\dfrac{{}_{n}C_{s}}{{}_{40}C_S} × \sum_{a=0}^{5}({}_5C_a × {}_{35-n}C_{S-s-a} )
$$
と変形できます。
この式を変形するために、ヴァンデルモンドの畳み込みという式を用います。
任意の負ではない整数$${p, q, n }$$に対して、
$$
\sum_{k=0}^{n} {}_pC_k × {}_qC_{n-k} = {}_{p+q}C_n
$$
という式が成立する。ただし、$${p < k}$$のとき、$${{}_pC_k = 0}$$とする。
この式の$${k→a, p→5, q→35-n, n→S-s}$$と見ると、
$${S-s > 5}$$のとき、
$${{}_5C_{S-s} = 0}$$であるから、
$$
\sum_{a=0}^{5}({}_5C_a × {}_{35-n}C_{S-s-a} ) = {}_{40-n}C_{S-s}
$$
と変形できます。よって、求めたい④の確率の式は、
$$
\dfrac{{}_{n}C_{s}}{{}_{40}C_S} × {}_{40-n}C_{S-s}
$$
と表すことができます。
⑤ ③/④を計算する
$$
\begin{align*}
③ &= \dfrac{{}_{n}C_{s}}{{}_{40}C_S} × {}_5C_a × {}_{35-n}C_{S-s-a} \\
④ &= \dfrac{{}_{n}C_{s}}{{}_{40}C_S} × {}_{40-n}C_{S-s}
\end{align*}
$$
であるので、
$$
\dfrac{\textcircled{3}}{\textcircled{4}} = \dfrac{{}_5C_a × {}_{35-n}C_{S-s-a}}{{}_{40-n}C_{S-s}}
$$
⑥ ⑤を用いて期待値を計算する
期待値は和の記号$${\sum}$$を用いて、
$$
\sum_{a=0}^{5}\left( \cfrac{{}_5C_a × {}_{35-n}C_{S-s-a}}{{}_{40-n}C_{S-s}} × a \right)
$$
と表されます。ここで、nとsはaに関係ない値なので、
$$
\dfrac{1}{{}_{40-n}C_{S-s}}\sum_{a=0}^{5}\left( {}_5C_a × {}_{35-n}C_{S-s-a} × a \right)
$$
と変形できます。ここでもヴァンデルモンドの畳み込みを使いたいところですが、最後の×aが邪魔です。そこで、次のような変形を行います。
$${5-a = 4-(a-1)}$$となることに注意です。
$$
\begin{align*}
&{}_5C_a × a \\
=& \frac{5!}{(5-a)! a!} × a \\
=& \frac{5×4!}{\left\{ 4-(a-1) \right\}!×a× (a-1)!}×a\\
=& 5×\frac{4!}{\left\{ 4-(a-1) \right\}! (a-1)!}\\
=& 5×{}_4C_{a-1}
\end{align*}
$$
よって、$${a'=a-1}$$として、
$${S-s-1 > 4}$$のときは$${{}_4C_{S-s-1} = 0}$$なので、
$$
\begin{align*}
&\sum_{a=0}^{5}\left( {}_5C_a × {}_{35-n}C_{S-s-a} × a \right) \\
=& 5× \sum_{a'=0}^{4}\left( {}_4C_{a'} × {}_{35-n}C_{(S-s-1)-a'} \right)\\
=& 5×{}_{39-n}C_{S-s-1}
\end{align*}
$$
よって、期待値は、
$$
\begin{align*}
&\frac{5×{}_{39-n}C_{S-s-1}}{{}_{40-n}C_{S-s}}\\
= & 5×\frac{(39-n)!}{\{(39-n)-(S-s-1)\}!(S-s-1)!}×\frac{\{ (40-n)-(S-s) \}! (S-s)!}{(40-n)!}\\
= & \cfrac{5×(39-n)!\{ (40-n)-(S-s) \}! (S-s)!}{\{(39-n)-(S-s-1)\}!(S-s-1)!(40-n)!}\\
= & \cfrac{5×(39-n)!(S-s)!}{(S-s-1)!(40-n)!}\\
= & \cfrac{5×(S-s)}{40-n}
\end{align*}
$$
証明は以上になります。
あとがたり
7月12日、カツキングcupの終盤、私は青単ジャバジャックのデッキを使用しており、レートは1697でした。
いわゆる魂の一戦の相手はシータ刃牙。
私はジャバが引けず、また相手の5ターン目にインテリジェンスが立ち、非常に苦しい展開でした。
刃牙を召喚されたときは😇😇となりましたが、マナゾーンに鬼丸覇は無し。それでも永遠とインテリを出され、リーサルをかけられ大ピンチ。
しかし、盾からアクアサーファーが…!

永遠をバウンスし、リーサルを逃れます。
帰ってきたターン、相手の盾は3枚。
私はエリートジャバ×2とキッドを出し、リーサルに行きましたが、盾には母なる大地が…!
インテリを出しなおされ、ゲームエンドとなりました…。
プレイの説明をすると、相手の盾に大地があるなら、エリートヴィルヴィスでインテリを戻さないといけません。ただし、その場合はサーファーでの1点で大地orドンドン吸い込むナウがあると、ジャバと違って選ばれるヴィルヴィスが処理され、リーサルがなくなってしまいます。
実はその数ターン前に2点入ったところ、大地(+ライフ)を踏んでいたこともあり、さすがにもう大地ないだろと思って、ジャバ×2で裏目を踏んでしまいました。
つまり、1点お祈りor3点大地なしのどちらの確率が高いのかという話です。
これを計算したくていろいろ考えて計算してみた結果、こんな長々とnoteを書くことになってしまいました😇
正直証明の④のnCrのかけ算にΣがついたあたりで詰みかけましたが、「Σ Cの積」とかで検索したところ、求めていたドンピシャの式変形が見つかり、大変助かりました。ありがとうヴァンデルモンドさん。
こたえあわせ
本当はインテリや刃牙のジャッジでもう何枚か見えていましたが、リプレイが流れてしまってわかりませんので、スクショからわかる情報だけで考えます。

◯条件
一旦、2点で踏んだライフと大地を墓地から盾に返して考えます。
手札2枚のうち1枚はバウンスした永遠ですが、もう1枚はわからないのでこれも山札に返します。
よって、盾5、公開カード18、山札17とします。
見えた(妨害)トリガーは、ドン吸い3枚と大地1枚(本当は2枚ですが、1枚シールドに返しています)です。
(1)盾に大地がある確率
[1] 18枚中1枚の大地が山札から見えた
[2] 盾5枚のうち2枚に大地が1枚あった
この二つの発生した事象をもとに、残り3枚の盾に大地がある確率を求めていきます。
[1]について計算を進めると、次のようになります。

①はゲーム開始時の確率です。
②は各場合に18枚中1枚見えるという事象が起こる確率
③は①と②の積、④は③の総和で、[1]の事象が起こる確率は30%ほどということになります。
この結果を用いて⑤では条件付き確率を求めています。
例えば、盾に2枚埋まってる確率は11.04%ということです。
[1]の事象が発生したことにより、盾の大地の枚数の確率が①→⑤と変化しました。以降この⑤を確率として使用します。
次に[2]について考えます。

まず、⑥として、各場合に2点で大地をちょうど1枚だけ踏む確率を考えます。これは単純で、5枚から2枚選ぶので、$${{}_5C_2 = 10通り}$$のうち、踏むパターンを考えればいいだけです。
⑦は⑤と⑥の積で、たしあわせたものが⑧です。[1]の状況下で、[2]が起こる確率は24.68%だったということです。
⑧が条件付き確率です。
これが本題であり、[1]かつ[2]が起こったという条件のもと、盾に大地が何枚あるかの確率になります。ただし、1枚はもう踏んでいるので、⑥のところのかけ算で0枚の確率は0%になっています。
よって、盾に大地がある確率は、26.84+1.58=28.42%
ちなみに当時、メイ様のナーフにより大地の採用枚数が減ってきていた時期でしたので、相手のデッキに大地が3枚しか入ってなかった場合も計算します。

こちらは15%となりました。
(2)ワンパンで(妨害)トリガーを踏む確率
[1] 18枚中4枚のトリガー(ドン吸い3、大地1)が山札から見えた
[2] 盾5枚のうち2枚にトリガー(大地)が1枚あった
(1)と同様に、この二つの発生した事象をもとに考えていきます。

⑨までは先ほどと同様ですが、今回はドン吸いも合わせて8枚で考えていますので、先ほどと確率が異なります。
次の行では、1点で踏む確率を求めています。4トリの場合は、残り全てがトリガーですので100%、3トリの場合は$${\tfrac{2}{3 }}$$で66%などと入った具合です。
このことも考え合わせると、⑩のようになり、最終的に⑩列の確率の総和である15%が1点でトリガーを踏む確率となります。
また、大地3枚採用の場合も計算すると、

この場合は10%となりました。
結果
大地がある確率が、28.42%または15%
1パントリガーの確率が、15%または10%
よって、17チャレ失敗は私の判断ミスでした😇
それでも、今回色々計算をきちんとするきっかけになってくれたので、解けたレート10以上の価値がある一戦だったと思います。
大変勉強になりました。
それでは、ここまで読んでいただき、本当にありがとうございました。確率・統計学は専門外のため、おかしな点もあるかと思います。お手柔らかにご指摘いただけるとありがたいです。
また機会がありましたら、なにか書きたいと思います。
この記事が気に入ったらサポートをしてみませんか?
