ある凡人の数学者人生が始まるまで 16

人それぞれという当たり前の話

人が数学を研究する理由は千差万別である。

皆が皆、数学が好きだから研究をしているとは限らない。使命を感じて数学を研究している人、数学が嫌いだが仕事だから仕方なく研究をしている人、別にやりたいわけではないけど生きていると呼吸をするかのようにいつの間にか次々と定理を証明してしまう人。

ここに書いた理由で数学を研究している人が本当にいるかはわからないが、人それぞれ様々な理由で数学を研究しているだろう。

数学は自由な学問であるとよく言われるが、携わり方にも大きな自由がある。それぞれが様々な理由で数学研究に携わり、その結果として全人類共有の知的財産である「数学の定理集」を作っている。

また、一口に「数学が好き」と言っても、数学のどのような側面が好きであるか、数学のどのような分野・対象が好きであるかも千差万別である。

問題を解こうと試行錯誤して考えているときが好きな人、問題が解けたときの快感が好きな人、数学の厳密性や論理的思考が好きな人、数学や定理の芸術性・美しさが好きな人、、、、

トポロジーが好きな人、微分方程式が好きな人、選択公理が好きな人、導来圏が好きな人、、、、

実に人それぞれであり、皆自分の感覚・感情を大事にすべきであると思う。しかし、数学への携わり方・感じ方を強制するような文章を書いたり言明することはよくないだろう。

数学のある定理や対象を美しいと感じる人がいるが、それを人に強制するような言明をしてはいけないと思う。

例えば（何故か）「オイラーの等式」と呼ばれることの多い次の定理がある：

私の場合は慣れすぎて、この定理には「自明感」を強く抱いてしまっているが、この定理を様々な理由で美しいと思う人がいたり、-1を左辺に移項すると美しいと感じる人がいたり、円周率の定義を変えた方がいいとか、何が美しいのかさっぱりわからないと感じる人がいたりするであろう。

そのような状態こそが健全であると思う。これを「世界で最も美しい公式」などと表現しているものを見かけることがあるが、それは強い主観であり人類皆が世界一美しいと思っているわけでは当然ない。「オイラーの等式には自然対数の底、円周率、虚数単位、加法単位元、乗法単位元という5つの基本定数が単純に結びついていることが美しい」などという表現を見かけることもあるが、それも個人の主観であって、「そう思えない人は数学ができない」とかそんなわけでは当然ない。

ただ、この定理を「世界一美しい公式だと思わなければならない」とか「5つの基本定数が結びついているから美しいことをあなたも理解しなさい」といった強制をしてはならないと強く思う。

「例えば」の話をしたが、このように数学への携わり方・感じ方を強制することはよくないことであると強く思う一方で、「美しいと感じた理由や気持ち」を各人は大事にしていいと思うし、私個人は「各人の数学に対する主観的感情」を割と積極的に知りたいと思っている。

ある数学者が特定の定理や数学的対象を「好きだ」とか「美しい」と感じ、その感情や視点が新しい定理の創造にプラスに繋がっていることがあるだろうと思う。

そのような感情を文章で表明してくださったり会話で聞ける場合、私はそれを読んだり聞いたりして、「同じように美しいと感じるかどうか」、「自分はその人とは異なる感情を抱くかどうか」等を考えることによって自分の今後の創造的活動の参考になると思っている。強制されたり鵜呑みにすることはよくないが、そうでなければ有効に利用できるだろう。

既にこの一連の文章でコーシーの積分定理を美しいと思ったことなどを表明しているが、包み隠さずに私自身の感情を述べているのは上述のような考え方を持っているからであり、これ以降もどんどん自分の好きな定理や美しいと思う感情を書いていくつもりである。鵜呑みにせず、「ふーん、あなたはそう思うのね」と思いながら読んでいただきたい。

私の好きな定理の種類

数多くある数学の定理の中で「好みの定理の型」がある人もいることと思う。

前述のオイラーの等式であったり、バーゼル問題を初めとする「無限級数の値」のような「等式で表現される定理」が好きな人もいるだろうし、「一般の5次以上の代数方程式が代数的には解けない」（アーベル・ルフィニの定理）のような「何かができないことを示す定理」が好きな人もいるだろうし、有限単純群の分類定理のような「何かを分類する定理」が好きな人もいるだろうし、志村・谷山予想とか岩澤主予想のような「異なる出自の2つの概念が思いがけず結びつく型の定理」が好きな人もいるだろう。

私も自己分析してみると「好みの定理の型」があることがわかる。それは強いて熟語で表現するならば

全称的存在定理

とでも言えるだろうか。

まず、存在定理と呼ばれる型の定理がある。Wikipediaの説明を引用すると、

存在定理（そんざいていり）とは、何らかの数学的対象の存在をいう定理の総称である。

とある。例えば、2019年にBookerさんによって証明された、方程式

が整数解を持つという定理は存在定理と言えるであろう。この定理は具体的に解を見つけるという形で証明された：

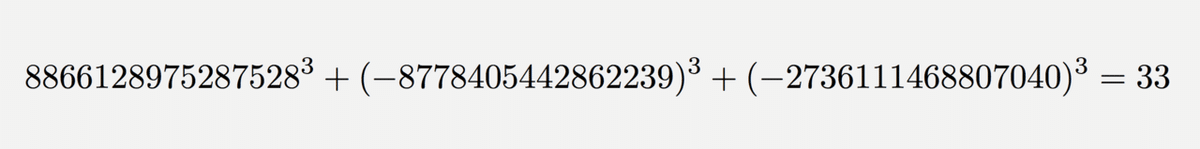
有名かつ私を数学の道へと誘ってくれたフェルマーの最終定理は解の非存在性に関する定理であり、それはそれで素晴らしい法則だと思う一方で解がないというのは寂しくも思う（数学は事実が最も大事なので私が寂しく思ったところでどうにもならないが）。ディオファントス方程式と呼ばれる類似の問題については、非自明な解があった方がその絶妙に存在する整数達を思うと嬉しくなったりする。有名どころでは

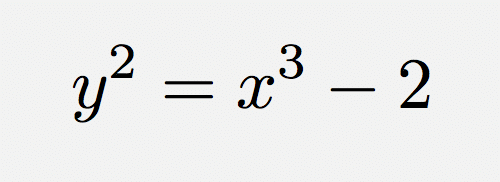
の自然数解がx=3, y=5に限るというフェルマーが発見した定理があって、これは「平方数、n、立方数」という自然数の連続する並びはn=26しかありえないということを示している。これを知って私は26という整数に愛着を抱くようになった。

また、2018年に慶応大学の松村君と平川君が証明した「辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には、周の長さと面積がともに等しい組が相似を除いて丁度１組だけ存在する」という存在定理は芸術性も非常に高い定理であると個人的には感じる。これも具体的な解が決定されている：

3辺が135, 352, 377である直角三角形と3辺が132, 366, 366である二等辺三角形はともに周の長さが864で面積が23760である。

もちろんディオファントス方程式は方程式によって解がなかったり、1個であったり、少しだけあったり、たくさんあったりする。そして、解が1つだけであるという定理を証明するということは、その1つ以外は解ではないということを証明することに他ならないので、フェルマーの最終定理と同様、解の非存在性にこそ証明上の重要性があると言えるかもしれない。それでも私は解が絶妙に1つしかないようなケースを目の前にすると感動してしまうようだ。

次に、全称命題と呼ばれる型の定理について。これはWikipediaには

全称命題（ぜんしょうめいだい、英：universal proposition）とは、一つの集合を構成する全ての項について、ある性質を肯定する命題である。

とある（項とあるのは以下では元と表現する）。ここでいう「一つの集合」が無限集合である場合、有限個の元を選んで各元について成立を調べたところでいつまでたっても証明されたことにはならない。それでも任意にとった元を対等に扱えるような議論を行うことによって証明できるような全称命題は数多くあり、数学の醍醐味の1つである。

全称命題の具体例については枚挙に暇がないが、「全ての直角三角形について、斜辺の長さの2乗は他の2辺のそれぞれの長さの2乗の和に等しい」という三平方の定理は全称命題である。例えば、3辺の長さが3,4,5である直角三角形や、5,12,13である直角三角形について（それらが直角三角形であることがわかっているものとして）3^2+4^2=5^2や5^2+12^2=13^2が成立することを確認することはできるが、このように具体例を確認しているだけではいつまでたっても証明できない一方で、全ての直角三角形について確かに成り立っていることを証明する上手い方法が多数知られている。

フェルマーの最終定理は「3以上の整数全体のなす集合」に属するnを指数とする全称命題と思うことができるが、全てのnで機能するような証明を見つけることが極めて困難なのであった。

私が好きな「全称的存在定理」とは全称命題の説明における「ある性質」が存在定理となっているような定理のことである。つまり、型としては

全ての○○に対して△△が存在して□□が成り立つ

と述べられるようなものである。

私は数学的存在性に感動することが多いが、無限集合に対する全称命題としての存在定理は「無限個の存在性を同時に主張する」ものなのである！そんな全称的存在定理であって「これは美しい！」と感じるものに私は幾つか出会ってきた。

大学初級レベルで学ぶ有名な全称的存在定理としては中間値の定理や代数学の基本定理があげられる。

整数論ではフェルマーの二平方和の定理が全称的存在定理の典型例であるし、先ほどは「意外な結びつき型定理」として紹介した志村・谷山予想は「任意の有理数体上定義された楕円曲線に対して或るモジュラー形式が存在して○○が成り立つ」と全称的存在定理として述べることもできる。

全称的存在定理は往々にして「具体的な構成法はわからないけど存在することだけは保障できる」という形で証明される。例えば5882353は4で割った余りが1であるような素数なので、上記定理によって2つの平方数の和として絶対に表すことができる。その一方で、典型的な証明はそれがどんな平方数であるかまでは教えてくれない。

もちろん、具体的な構成法までわかった方が数学の定理としては強いし応用もしやすくなるため、存在性のみがわかった後に具体的な構成法を模索するというのは重要かつよくある研究の方向性と言える（時には特定の方法では構成することが不可能であるという型の定理が証明されることもあるだろう）。

数学的にはそのように研究を進めるのが重要であることは頭ではわかっているんだけど、全称的存在定理の「存在することだけがわかっている」状態が私はすこぶる好きで、美しさやロマンを感じることがある。

「具体的にどんなものかは誰も知らないのに、あることだけは確かである」

その存在に思いを馳せるのが私は大好きだ。