
【ABC362】緑コーダーの競プロ参加記録 #28
今回はAtCoder Beginner Contest 362。使用言語はPythonです。

A問題 - Buy a Pen
コンテスト中の提出
https://atcoder.jp/contests/abc362/submissions/55511894
3種類のペンがあり、それぞれ$${R, G, B}$$円。
$${C}$$以外のペンの金額のうち、最小の金額を出力してね。
与えられる3種類の$${C}$$それぞれについて、if 文を使って異なる処理を行います。
残りの2つのペンの金額のうち小さい方の金額を出力すればよく、これは min 関数 を使うことで実現できます。
""" AC コード """
R, G, B = map(int, input().split())
C = input()
ans = 0
if C == 'Red':
ans = min(G, B)
elif C == 'Green':
ans = min(R, B)
else:
ans = min(R, G)
print(ans)$${R,G,B \le 100}$$であることを利用して、ペン$${C}$$の金額を大きな数に更新する解き方もあります。
Python の min 関数は、引数が3つ以上でも使うことができます。
""" ペン C の金額を、他の2つより大きいことにする """
R, G, B = map(int, input().split())
C = input()
if C == 'Red':
R = 99999
elif C == 'Green':
G = 99999
else:
B = 99999
ans = min(R, G, B)
print(ans)B問題 - Right Triangle
コンテスト中の提出
https://atcoder.jp/contests/abc362/submissions/55525250
3点$${A, B, C}$$の座標が与えられる。
三角形$${\mathrm{ABC}}$$が直角三角形かどうか判定してね。
入力の時点では、どの角が直角になっているか分かりません。
角$${A, B, C}$$のうちどれが直角であるか、考えられる3パターンすべてについて判定を試します。

例えば、角$${A}$$が直角であるとして「$${x_a = x_b}$$かつ$${y_a = y_c}$$」のような判定方法が思い浮かびます。
しかし、三角形はナナメになっていることもあるので、これでは不十分です。
判定については、公式解説にある通り、三平方の定理を利用することができます。

それぞれの辺の長さを求めるとき、math.sqrt 等を使って2乗を外す必要はありません。
というよりも、2乗を外すと小数誤差で WA になります。
競プロでは可能な限り整数のまま扱うことが重要です。
def length(A, B):
""" 線分 AB の 長さの2乗 を求める """
xa, ya = A
xb, yb = B
return (xa - xb) ** 2 + (ya - yb) ** 2
def solve(A, B, C):
""" ∠ABC が直角かどうか判定 """
AB = length(A, B)
BC = length(B, C)
AC = length(C, A)
return AB + BC == AC
""" 入力を受け取る """
A = tuple(map(int, input().split()))
B = tuple(map(int, input().split()))
C = tuple(map(int, input().split()))
""" ∠BAC, ∠ABC, ∠ACB についてそれぞれ調べる """
ok = False
ok |= solve(B, A, C)
ok |= solve(A, B, C)
ok |= solve(A, C, B)
""" 答えを出力 """
if ok:
print('Yes')
else:
print('No')やや難しい内容になりますが「ベクトルの内積」を利用して解くこともできます。
興味がある方は調べてみてください。
私の提出コードはこちらの方法で解いています。

C問題 - Sum = 0
コンテスト中の提出
https://atcoder.jp/contests/abc362/submissions/55538272
$${N}$$個の整数の組$${(L_i, R_i)}$$が与えられる。
条件 1: すべての$${i}$$について$${L_i \le X_i \le R_i}$$
条件 2: $${\displaystyle\sum_{i=1}^NX_i = 0}$$
条件を満たす整数列$${X}$$があれば、1つ出力してね。
「ある値を作りたいとき、下限と上限の間はすべて作れる」という考察テクニックをもとにした問題になっています。

数列 X の要素の総和を 0 にできる?
$${\displaystyle\sum_{i=1}^NX_i}$$について、最小値・最大値を考えてみます。
$${L_i \le X_i \le R_i}$$なので、$${X_i = L_i}$$とすれば$${X}$$の$${i}$$番目の要素として考えられる最小の整数を選ぶことができます。
これをすべての$${i}$$について繰り返すことで、$${\displaystyle\sum_{i=1}^NX_i}$$を最小にすることができます。
最大値についても同様に、$${X_i = R_i}$$とすることで達成できます。
ここで、$${\displaystyle\sum_{i=1}^NX_i}$$の最小値・最大値をそれぞれ$${S, T}$$とします。
このとき、$${S \le 0 \le T}$$でなければ$${\displaystyle\sum_{i=1}^NX_i = 0}$$とすることができません。
""" 入力を受け取る """
N = int(input())
P = [tuple(map(int, input().split())) for _ in range(N)]
""" sum(X) の最小値 S と、最大値 T を求める """
S, T = 0, 0
for L, R in P:
S += L
T += R
""" S <= 0 <= T でないなら NG """
if not(S <= 0 <= T):
print('No')
exit()「$${X}$$の要素の総和としてありうる整数の範囲に$${0}$$が含まれている必要がある」と考えるとイメージしやすいです。
$${L_i \le R_i}$$の制約から、$${S \le T}$$であることは保証されています。
数列 X はどうやって作る?
最初、すべての$${i}$$について$${X_i = L_i}$$とします。
このとき$${\displaystyle\sum_{i=1}^NX_i = S (\le 0)}$$です。
ここで、ある$${i}$$について、$${X_i}$$の値を$${L_i}$$から増加させた分だけ$${X}$$の総和の値も増えます。
つまり、$${a_i \ge 0}$$かつ$${L_i + a_i \le R_i}$$を満たす整数$${a_i}$$について$${X_i = L_i +a_i }$$とすると、$${\displaystyle\sum_{i=1}^NX_i = S + \displaystyle\sum_{i=1}^Na_i}$$となります。
よって、$${X}$$の総和を$${0}$$にするための不足分を全体で補えばよく、その不足分は$${\displaystyle\sum_{i=1}^Na_i = -S}$$です。
$${i}$$の昇順に$${\displaystyle\sum_{i=1}^ja_i = -S}$$となるまで十分に加算したあとは、残りの$${i > j}$$について$${a_i=0}$$とすればよいので、$${L_i}$$からの増加分$${a_i}$$は可能な限りの大きな値を貪欲に選択してよいです。
具体的には、現在の不足分$${-S_i}$$に対して、$${a_i = \min(R_i - L_i, -S_i)}$$となります。
""" x = L をベースに、足りない分だけ x を大きくする """
ans = []
for L, R in P:
a = min(R - L, -S)
x = L + a
S += a
ans.append(x)
""" 答えを出力 """
print('Yes')
print(*ans)D問題 - Shortest Path 3
コンテスト中の提出
https://atcoder.jp/contests/abc362/submissions/55542627
$${N}$$頂点$${M}$$辺の無向グラフが与えられる。
$${i}$$番目の頂点はコスト$${A_i}$$。
$${i}$$番目の辺は頂点$${U_i, V_i}$$を結び、コスト$${B_i}$$。
$${2 \le i \le N}$$について、頂点$${1}$$から頂点$${i}$$までの最小コストを出力してね。
$${0 \le A_i, B_i \le 10^9}$$であり、コストに負の値は含まれません。
頂点のコスト$${A_i}$$がなければ、典型的な「すべての辺のコストが等しいとは限らない場合の最短経路問題」であり、ダイクストラ法で解くことができます。
そして、通常のダイクストラ法に「頂点のコスト」を追加で考えることで、この問題も解くことができます。
from heapq import *
def dijkstra(start):
""" 頂点 start からの最小コストを求めるダイクストラ法 """
hq = [(A[start], start)]
inf = 1 << 60
dist = [inf] * N
dist[start] = A[start]
while hq:
d, curr = heappop(hq)
if d > dist[curr]:
continue
for nxt, cost in G[curr]:
if dist[nxt] > dist[curr] + A[nxt] + cost:
dist[nxt] = dist[curr] + A[nxt] + cost
heappush(hq, (dist[nxt], nxt))
return dist
""" 入力を受け取る """
N, M = map(int, input().split())
A = list(map(int, input().split()))
G = [[] for _ in range(N)]
for _ in range(M):
u, v, b = map(int, input().split())
u -= 1; v -= 1 # 0-indexに変換
G[u].append((v, b))
G[v].append((u, b))
""" 頂点 0 から各頂点までの最小コストを調べる """
dist = dijkstra(0)
""" 答えを出力 """
print(*dist[1:])上記コードでは、$${A}$$とインデックスを揃えるために頂点の番号を 0-index に直しています。
書くことが少なかったので、ダイクストラ法の学習の際に参考になる記事をご紹介します。
01-BFS の解説記事ですが、その中で「BFS とダイクストラ法は実は同じことをしている」ということが説明されており、これらのアルゴリズムに対する理解の助けになります。
ダイクストラ法の説明も丁寧で分かりやすく、ダイクストラ法をこれから学ぶ方にも、すでに習得している方にもぜひ読んでみていただきたいと思います。
E問題 - Count Arithmetic Subsequences
コンテスト中の提出
https://atcoder.jp/contests/abc362/submissions/55558371
長さ$${N}$$の数列$${A}$$が与えられる。
$${1 \le k \le N}$$について、$${A}$$の長さ$${k}$$の部分列が等差数列であるものの個数を出力してね。$${\pmod{998244353}}$$
長さ$${1}$$または$${2}$$の数列は、すべて等差数列です。
よって、条件を満たす長さ$${1, 2}$$の部分列の個数はそれぞれ$${N, _NC_2}$$です。
""" 入力を受け取る """
N = int(input())
A = list(map(int, input().split()))
mod = 998244353
""" 長さ 1, 2 の数列はすべて等差数列 """
if N == 1:
print(N)
exit()
ans = [0] * N
ans[0] = N
ans[1] = N * (N - 1) // 2 % mod等差数列では「長さ$${k}$$、末尾の値$${x}$$、公差$${d}$$であるような数列」があったとき、「その末尾に$${x+d}$$を追加した長さ$${k+1}$$の数列」を新たに作ることができます。
新たに作られる長さ$${k+1}$$の数列の個数は、長さ$${k}$$の数列の個数から求めることができ、DP の香りがしてきます。

ところが、$${A_i \le 10^9}$$であり、DP リストに末尾の値$${x}$$や公差$${d}$$を持てそうにありません。
ここで、数えたい等差数列の項の値は$${A}$$の要素のどれかであり、末尾の情報はインデックスを持つだけでよさそうです。
長さ$${k}$$はそのまま持てることを考えると、この他に初項の情報があれば公差$${d}$$を逆算することができます。
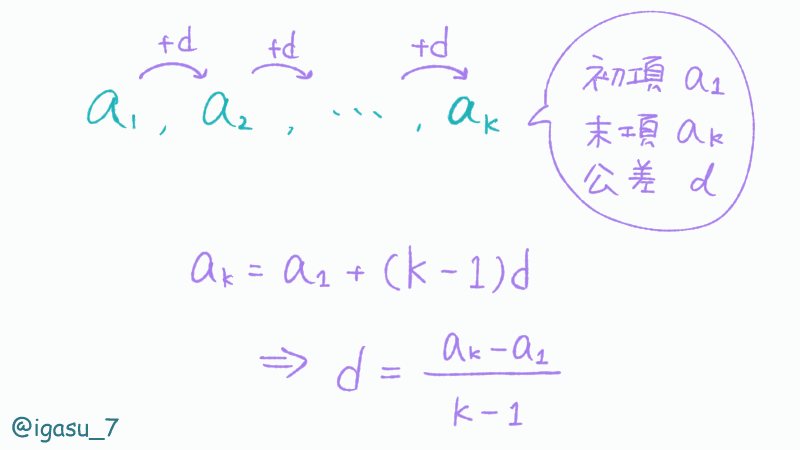
つまり、以下のようなDPになります。
$$
dp[i][j][k]: 初項A_i, 末項A_j,長さkの等差数列の個数
$$
公差$${d=\displaystyle\frac{A_j -A_i}{k -1}}$$となり、$${j < u}$$かつ$${A_u = A_j + d}$$を満たす$${u}$$が存在するとき DP の遷移を行います。
追加後の数列は「初項$${A_i}$$、末項$${A_u}$$、長さ$${k+1}$$」になるため、遷移は以下のようになります。
$$
dp[i][u][k + 1] \xleftarrow{+} dp[i][j][k]
$$
"""
dp[i][j]: 初項 A[i], 末項 A[j], 項数 k の等差数列の個数
公差 d = (A[j] - A[i]) // (k - 1)
k = 2 について初期化
"""
dp = [[0] * N for _ in range(N)]
for i in range(N):
for j in range(i + 1, N):
dp[i][j] = 1
""" k > 2 以降を DP で求める """
for k in range(2, N):
ndp = [[0] * N for _ in range(N)]
for i in range(N):
for j in range(i + 1, N):
if dp[i][j] == 0:
continue
d = (A[j] - A[i]) // (k - 1) # 等差数列がある => (k - 1) で割り切れる
""" 末尾に A[u] を追加 """
for u in range(j + 1, N):
if A[j] + d == A[u]:
ndp[i][u] += dp[i][j]
""" 答えを更新 """
for i in range(N):
for j in range(i + 1, N):
dp[i][j] = ndp[i][j] % mod
ans[k] += dp[i][j]
ans[k] %= mod # ans[k] は 0-index
print(*ans)今回、$${k}$$は1つ前のものしか参照しないため、DPリストを分割して実装しています。
公式解説の$${O(N^4)}$$解法では隣り合う2項から公差$${d}$$を逆算しています。
また、「先頭に$${A_i}$$を追加する」操作をしているので初項$${i}$$を降順に走査しています。
イメージしやすい方で実装してみてください。
あとがき
今回は ABCDE 5完 1ペナ 70分で 1729位でした。
図形の問題がいちばん苦手なのでB問題レベルでもかなり苦しい。
四角形になると、もうお手上げです。
ではまた~。


【更新履歴】
2024/07/14 (12時頃):記事投稿。
この記事が気に入ったらサポートをしてみませんか?
