ネイピア数のx乗を微分する

ネイピア数は次の通りあらわすことができました。

$${\displaystyle e = \lim_{x\to \pm\infty} \left(1+\frac{1}{x} \right)^{x}=\lim_{x \to 0} (1+x)^{\frac{1}{x}}}$$

ここで$${\displaystyle\frac{1}{x}}$$を$${\displaystyle\frac{a}{x}}$$にすると、次のとおり変形することができます。$${\displaystyle\lim_{x\to \pm\infty} \left(1+\frac{a}{x} \right)^{x}=\lim_{x \to 0} (1+ax)^{\frac{1}{x}} =e^a }$$

なぜなら、$${\displaystyle \frac{x}{a}=t(a\ne0)}$$とおくと、$${x=at}$$だから、

$${\displaystyle\lim_{x\to \pm\infty} \left(1+\frac{a}{x} \right)^{x}=\lim_{t\to \pm\infty} \left(1+\frac{a}{at} \right)^{at}=\lim_{t\to \pm\infty} \left\{\left(1+\frac{1}{t} \right)^{t}\right\}^a=e^a}$$$${a=0}$$なら、$${\displaystyle\lim_{x\to \pm\infty} \left(1+\frac{a}{x} \right)^{x}=1^0=1,=e^0=1}$$となり正しくなります。

早速グラフにすると計算結果が正しいことがわかります。

import matplotlib.pyplot as plt
import numpy as np
plt.style.use('seaborn-poster')
alphas=[0.2,1,1]
widths=[7,1,1]
num=2
pitch=0.001
x=1000
a = np.arange(-num,num+1,pitch) #グラフの作成 
formula=[(1+a/x)**x, np.e**a]

labels = [r'$\left(1+\frac{a}{x} \right)^{x}$',r'$e^a$']
colors=['r','b']
plt.figure(figsize = (10,8))
for fx, label, color ,alpha, w in zip(formula, labels,colors,alphas,widths):
   plt.plot(a,fx, color, label = label ,alpha=alpha,linewidth=w)
plt.grid()
plt.title(r'$\left(1+\frac{a}{x} \right)^{x},e^a$のグラフ',fontname="MS Gothic")
plt.xlabel('a')
plt.ylabel('y')
plt.ylim(0,30)
plt.legend()

ネイピア数のx乗の微分係数（$${e^x}$$）は次の通り、全く同じ$${e^x}$$になります。

$${\displaystyle\frac{d}{dx}e^x=\displaystyle \lim_{h\to 0}\frac{e^{x+h}-e^x}{h} =e^x\lim_{h\to 0}\frac{e^{h}-1}{h}=e^x}$$

グラフにすると次の通りになります。

import matplotlib.pyplot as plt
import numpy as np

def  tangent_line(x,val):
   dif=np.e**val*(x-val)+np.e**val
   return  np.where((np.e**val*0.7<dif)&(dif<np.e**val*1.3),dif,np.nan)

plt.style.use('seaborn-poster')
alphas=[0.6,1,1,1]
widths=[2,2,2,2]
start=-2
end=3
pitch=0.001
x = np.arange(start,end+1,pitch)
dif0=tangent_line(x,0)
dif1=tangent_line(x,1)
dif2=tangent_line(x,2)
# dif #グラフの作成 
formula=[np.e**x,dif0 ,dif1,dif2]
labels = [r"Napier's constant",r'$x=0$',r'$x=1$',r'$x=2$']
colors=['r','b','b','b']
plt.figure(figsize = (10,10))
for fx, label, color ,alpha, w in zip(formula, labels,colors,alphas,widths):
   plt.plot(x,fx, color, label = label ,alpha=alpha,linewidth=w)
plt.grid()
plt.title(r'ネイピア数のx乗と微分係数',fontname='MS Gothic')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(0,10)
plt.xticks(np.arange(min(x), max(x)+1, 1.0))
plt.yticks(np.arange(0,11, 1.0))
plt.legend()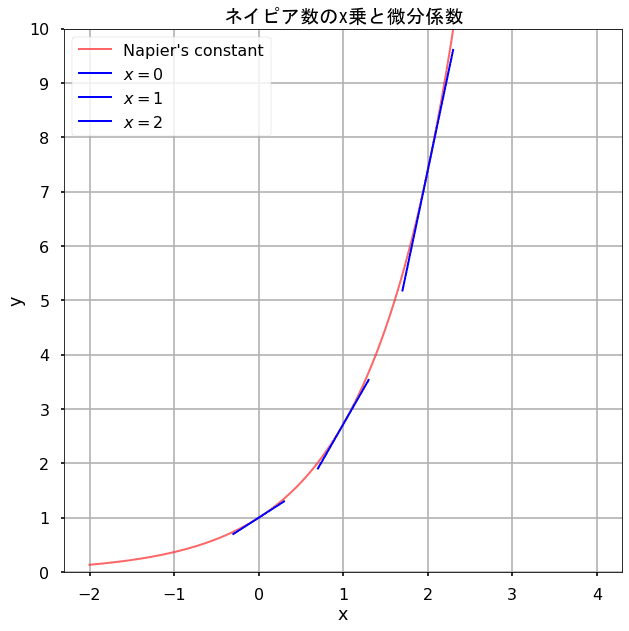   

xには求める乗数を-2から4まで0.001刻みでndarray形式で定義します。これに対し、$${x=-1,0,1,2}$$の接線を引いています。接線の配列はtangent_line関数で計算しています。