
ニューラルネットワークの活性化関数
ニューラルネットワークでは一般にユニットから次の層のユニットに値を渡す前にに活性化関数を通します。現在、一般に使われる活性化関数は次の5種です。
1.恒等関数

$${I(x)=x}$$
値をそのまま伝える関数です。活性化の働きはありませんが、これも活性化関数の1種。
2.ステップ関数(ヘヴィサイド関数)

とても単純な活性化関数。式で書くと

となります。値が小さいときには0、しきい値を超える1というものです。ニューラルネットワークが神経回路網を模しているとすると、神経への刺激がある値を超えると次に伝達する、ということを表しています。
3.ロジスティック関数(シグモイド関数)


シグモイドというのは「S字型」を意味する語です。したがって正確にはシグモイド関数とはS字型曲線となる関数の総称ですが、このロジスティック関数をシグモイド関数と呼ぶことも多いです。フェルフルストの人口動態モデルから導き出される式であり、この関数で現れる現象が多々あります。C∞級関数(無限回微分可能)であることや

を満たすなど、数学的によい性質を持つ関数です。
4.tanh(双曲線正接関数・ハイパボリックタンジェント)
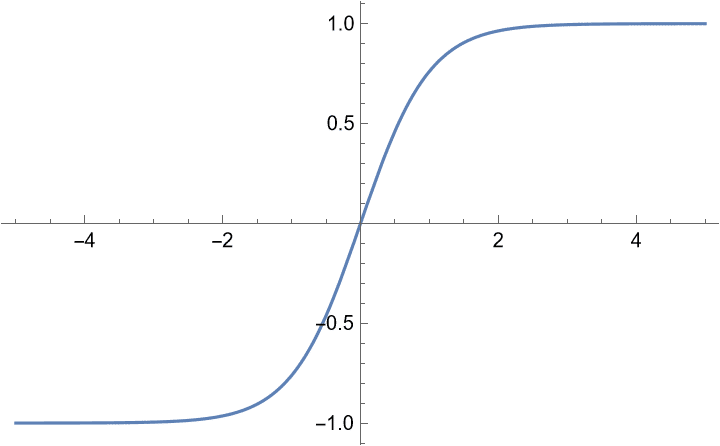

「タンエイチ」とか、情報系の方などには「タンチ」と呼ばれている関数です。2のロジスティック関数と別に紹介されることが多いですが、実は次の式が示すように、ロジスティック関数をx軸方向に1/2倍して、y軸方向に2倍して、y軸方向に-1移動した関数であり、このユニットの出力の重みパラメータを変えることで実現できるため本質的にはロジスティック関数とtanhは活性化関数としては同等な関数です。値域が(-1,1)となっており正負にバランスよく値を取ることからtanhが好まれることがあるようです。

ロジスティック関数と同様、次のような扱いやすい性質を持っています。

5.ReLU

「レルー」「レル関数」と呼ばれます。数学では「ランプ関数」と呼ばれます。グラフはカバー画像。しきい値を超えると値が線形に増加する関数です。x>0、つまり広い範囲で一定の勾配を持つため学習が早く進みます。したがって、活性化関数としてReLUを使うと、収束が早くなったり性能がよくなることが多く、現在最もよく使われています。デメリットとしては値の小さいところでは微分が0であるため、学習の途中でここにひっかかってしまうと重みの更新がなされず、このニューロンがDead Neuron となることです。

とかけることからもわかるように、恒等関数の負の部分を truncate したものです。
6.PReLU(Parametric ReLU)


のデメリットを解消するために a=0.01とした Reaky RELU が提案され、これを傾きをパラメータ化して一般化したものです。a も一緒に学習します。Reaky RELUではあまり改善が現れなかったものが、これにより性能が改善されたと報告されています。ちなみに Reaky はリーク=漏れるの意味です。x<0 でも勾配を持つため、学習が止まることがありません。
ほかにも、PReLUのような考え方でx<0にも勾配を持たせた活性化関数がいくつか提案されています。
この記事が気に入ったらサポートをしてみませんか?
