
史上最強の準優勝
秋場所の初日が近づいてきました。
白鵬が出るとか出ないとかもありますが、やはり場所前の話題は稀勢の里の綱取り。成るか成らぬか待ったなし(と言ってもう数場所引っ張ってますが)
そんななか、一部から「もう3場所も連続で準優勝してるんだから、秋場所もそのくらいの成績だったら、優勝なしでも横綱推挙でいいんじゃない?」という意見が。
ご存じのとおり、横綱審議委員会の横綱推挙の条件とされているのは「大関で2場所連続優勝またはそれに準ずる成績」
毎度問題になるのは、この「それに準ずる成績」がどの程度かってこと。たとえば4場所連続準優勝ってのは、「準ずる」んでしょうか、どうなんでしょうか。
そこで、例によって過去の準優勝者を調べてみました。
とはいっても、これけっこう大変。
というのも、じつは「準優勝」って、大相撲の表彰規定にはないんですよ。「準優勝」って言葉も比較的新しいらしい。先の横綱推挙の「準ずる」が出てからの言葉みたい。それまでは「優勝次点」とかいってたみたいですね。
なので、各場所の準優勝者をまとめた資料は、ほとんどないのです。仕方ないので、コツコツ調べましたよ。
色々制度が変わってメンドクサイ面もあるので、今回は昭和22年(1947年)夏場所の優勝決定戦制度施行以後の場所に限りました。
さて優勝回数の一覧表はよく見るでしょうが、(たぶん)史上初の「準優勝回数一覧表」 その上位はこうなっています。(黄色は現役力士)
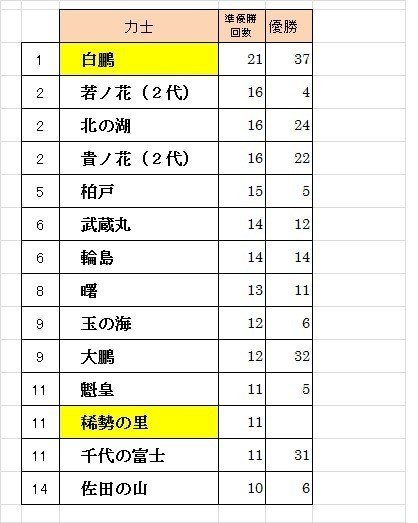
はい、準優勝を10回以上成しとげた力士は、この14人だけ(これ以前は場所数も少ないので、たぶんこれに食い込む力士はいないと思われます)
さすがに名だたる名力士が揃っていますね。右側に優勝回数も添えましたが、やはり準優勝が多い力士は、優勝も多いんだな……いやいや、ちょっと待てよ。
優勝回数トップの白鵬がここでもトップなのはうなずけるのですが、優勝回数第2位(32回)の大鵬は9位(準優勝12回)に、第3位(31回)の千代の富士は11位(準優勝11回)に沈んでいます。さらに優勝25回の大横綱・朝青龍は圏外(準優勝は8回)
逆に優勝回数わずか4回の2代目・若ノ花(若三杉)が準優勝16回で、北の湖(優勝24回)、2代目・貴ノ花(優勝22回)という大横綱たちと並んでいますし、大鵬のライバルだった柏戸(優勝5回)は準優勝回数では大鵬よりも上位にランクしているのです(準優勝15回) また志半ばで夭逝した玉の海(優勝6回)も準優勝では12回をスコアしています。
そして、横綱にはなれなかった魁皇(優勝5回)も、準優勝回数では堂々のランクイン(準優勝11回)。
こうして見ると、2代目・若ノ花、柏戸、玉の海、魁皇あたりが大相撲史上に残る「シルバーコレクター」ということでしょうか。
いやいや、ここですごいのが、じつは稀勢の里。
ご覧のとおり、この準優勝回数上位ランキングで、ただ一人、優勝がない。もう準優勝ばっかり。これぞ正真正銘のシルバーコレクターですね。
優勝回数が少ないのに準優勝が多いのは、毎度毎度「惜しかった」が多いってこと。2代目・若ノ花には同年齢の北の湖が、柏戸、玉の海には大鵬が、魁皇には2代目・貴ノ花あたりが、いつもドーンと壁となって立ちはだかり、彼らの優勝をあと一歩のところでかっさらい続けたからでしょうね。もちろん、稀勢の里にとっては白鵬がその「壁」なのです。
それに対して、朝青龍の準優勝が少ないのは、それだけ壁となる力士がおらず、実力が突出していたから、そしてここぞというときの狙いは逃がさない執念があったからでしょう。うんうん、そうだろうなぁ。
さて、冒頭に戻って「稀勢の里が4場所連続準優勝ならば横綱昇進は妥当なのか」という命題ですが、今回こうして調べてみると、3場所くらいの連続準優勝はけっこうある、けっして珍しくも偉業でもないってことがわかりました。
いちいち挙げると大変なので、決定的な例を紹介しちゃいましょう。
1988年(昭和63年)の9月場所から翌年の5月場所まで、旭富士は実に5場所連続準優勝に輝いています。
この間の優勝は、千代の富士が3回、北勝海が2回と、九重部屋最強横綱コンビが立ちはだかってました。
そんななか、じつはこの連続準優勝記録が始まる前、その年の5月場所も旭富士は準優勝しているのです。これはけっこうスゴイ。しかもしかも、同じ年の1月場所ではなんと初優勝も遂げています。9場所中7場所で準優勝以上。これすべて大関の地位での記録です。
にもかかわらず、この時の旭富士は横綱にはなっていません。
旭富士が横綱になったのは、1990年になってから。同年の5月場所と7月場所で文句なしの連続優勝を遂げてからでした(旭富士の準優勝は通算9回) ね、いくら稀勢の里を横綱推挙の意見が出ても、元・旭富士の伊勢ヶ濱親方が許さないでしょ。
稀勢の里さん、やはり優勝しないとダメみたいですよ。
準優勝の記録はいろいろ面白いので、次回もうちょっと続けましょう。
