技術士 一次過去問…解析：有限要素法

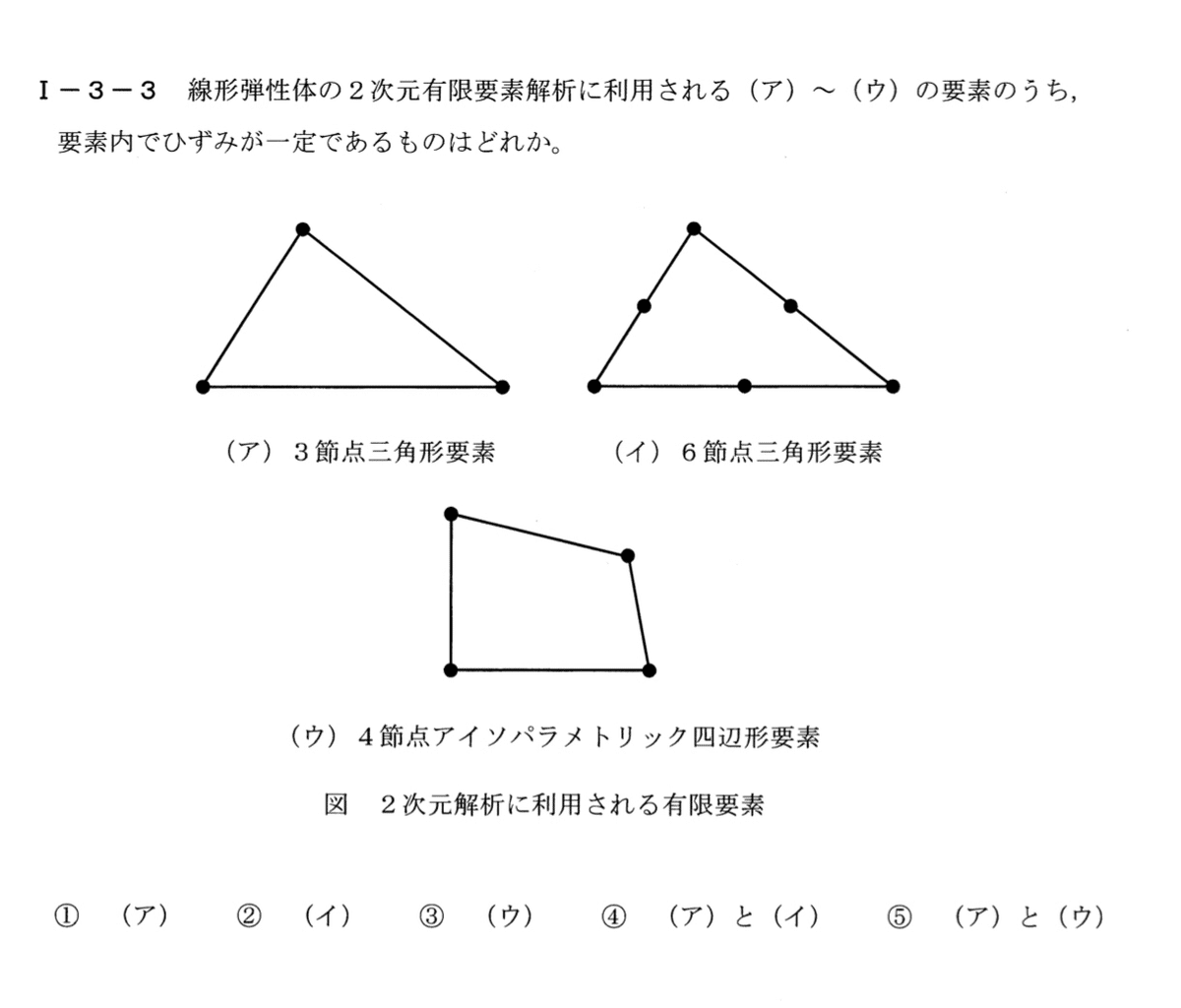
令和３年度 基礎科目 3群…解析

mono塾…ものコラム：線形解析において誤差が大きくなる要因を把握しよう
https://d-monoweb.com/blog/error-linear-analysis/

株式会社ストラクチャー
早わかり有限要素法 その1
https://www.structure.jp/column44/column44_1.html
早わかり有限要素法 その2
https://www.structure.jp/column44/column44_2.html

有限要素法では εx を
　　εx = [ B ] { ue }
のように書きます。
この [ B ] は 「節点変位からひずみを求める」もので、ひずみ - 変位マトリクス です。
既述のように、[ B ] には位置 x の情報は含まれず、具体的に書くと
　　( 1 / L ) [ -1　1 ]
ですが、この値は、先ほどの形状係数 [ N ] の成分を x で微分したものであることが分かるでしょう。

ひずみ εx は一定なので、これをあらためて ε とすると、ここから応力 σ は
　　σ = [ D ] ε
で得られます。
この [ D ] は 「ひずみから応力を求める」もので、応力 - ひずみマトリクス です。
さらに、ここに ε = [ B ] { ue } を代入して
　　σ = [ D ] ε = [ D ] [ B ] { ue }
とすると、これが「応力と節点変位の関係」です。
で、それからどうするのかというと、これでようやく要素の剛性マトリクス [ Ke ] が作れるのですが、これについては「その 4」で取り上げることにします。

上記の 株式会社ストラクチャー 早わかり有限要素法 その2より

コグニカル
内積と転置行列の関係
https://cognicull.com/ja/o5cjhfuf
仕事(物理学)…距離mはベクトルの変位の絶対値？
https://cognicull.com/ja/3c2etst8

ヨビノリ
ベクトル解析入門①(内積と外積)
https://www.youtube.com/watch?v=k7ImHQhxF3s

CAE(Computer Aided Engineering)
CADとシュミレーションソフトで、色々シュミレーションしてみることらしい
(hana超訳)

CAEと強度計算の森
https://www.fem-vandv.net/index.html
https://www.fem-vandv.net/c18.html

RTデザインラボ
有限要素法詳細
→ ページの一番下：有限要素法で使われる要素 (問題文のような図と解説あり)
https://www.rt-designlab.com/c4.html#:~:text=%E3%81%B2%E3%81%9A%E3%81%BF%E3%81%AF%E5%A4%89%E4%BD%8D%E3%82%92%E5%BA%A7%E6%A8%99%E3%81%A7%E5%BE%AE%E5%88%86%E3%81%97%E3%81%9F%E3%82%82%E3%81%AE%E3%81%AA%E3%81%AE%E3%81%A7,%E3%81%A8%E5%90%8D%E5%89%8D%E3%82%92%E4%BB%98%E3%81%91%E3%81%BE%E3%81%99%E3%80%82

弾性体のひずみは変位を座標（ｘ，ｙ）で偏微分したものであるため

上記のRTデザインラボ - 有限要素法詳細の始めのあたり

Trans Simulation…有限要素法（FEM）とは？基礎から解析の流れをまとめてご紹介
https://x-simulation.jp/blog/17#:~:text=%E6%9C%89%E9%99%90%E8%A6%81%E7%B4%A0%E6%B3%95%EF%BC%88Finite%20Element,%E3%82%92%E8%A7%A3%E6%9E%90%E3%81%99%E3%82%8B%E6%89%8B%E6%B3%95%E3%81%A7%E3%81%99%E3%80%82

筑波大学…有限要素法（FEM）による要素節点変位からのひずみと応力の算出
http://www.kz.tsukuba.ac.jp/EME/opensource/FEM.html