
自然言語処理⑩~Simple RNN・LSTM入門~
いよいよ自然言語処理に戻って行きます。
とはいえ、RNNは掘れば掘るほどいかついので、ここでは踏み込みすぎない程度の説明になってしまうかなと思います(現時点では。)
では、今回は以前も書いたのですが、SimpleRNNの実装とそれが何を意味しているのかをおさらいしつつ、LSTMとかその他もろもろ進めて行きます(ちょっとどうやって進めていくかが’まとまってないので、書きながら構成します。)
では、今回もよろしくお願いいたします。
・SimpleRNNの実装
いきなり実装してみます。
SimpleRNNというkerasの中に用意されたものがあるので、それを使って行きながら、まずはRNNに触れることから始めます。
自分も理解に苦しんだ部分で、コードの後に、何をしているのか図で説明して行きます。
本当にSimpleRNNのコードとか書いてるサイトとかあるのですが、どれも「(素人からすれば)なんかわかんない!」って感じになったので、本当にゆっくり解説しようと思います。
今回はsin curve(サインカカーブ)をSimple RNNを使って予測します。
(なんでsin関数なの?っていうのは、素人考えですが、物理の波とかでsinが使われたりするので、擬似的に時系列(シーケンス)として見ることができるからかなと。)
まず、データを手動で準備します。
np.random.seed(1)
timeline = np.linspace(-2*np.pi, 2*np.pi)
sin_data = np.sin(timeline) + 0.1 * np.random.randn(len(timeline)) # ノイズを0~1の正規分布の乱数で加える
plt.plot(timeline, sin_data)
plt.show()
ここからSimpleRNNを使うためにデータをいじります。
# シーケンスの長さ
n_rnn = 10
# サンプル数
n_samples = len(timeline) - n_rnn
# 入力と正解データの準備
X = np.zeros((n_samples, n_rnn))
t = np.zeros((n_samples, n_rnn))
for i in range(0, n_samples):
X[i] = sin_data[i:i+n_rnn]
t[i] = sin_data[i+1:i+1+n_rnn]
X = X.reshape((n_samples, n_rnn, 1))
t = t.reshape((n_samples, n_rnn, 1))シーケンスの長さを自分で決めます。
(「シーケンスの長さ」っていうのがピンとこず、解釈がしっくりこなかったです。正確性を無視すれば、どれくらい遡るのか?って感じです。つまり今回なら10個前のデータまで参照するイメージ。)
そして、サンプル数はシーケンスの長さを考慮してデータ数からシーケンスの長さを引きます。
(噛み砕くと、最初の10個のデータは前にデータが10個もないので、分析できるのは11~len(timeline)までとなる。)
そして、X, tに空(=0)のデータ枠を用意して、sin_dataから10個とって行きます。
tに関してはxの要素の次の値から10個をとってきます。
そして、最終的にreshapeしています。
ピンとこないと思うので、ざっと図にすれば以下。



(この辺、ちょっとTensorっぽい??)
わかりにくいとは思いつつ、困ったらcodeをみた方が早いかもです。
では、SimpleRNNを作りcompileとかsummaryを見て行きます。
batch_size = 10
num_epochs = 20
n_input = 1
middle_units = 20
n_out = 1
model = tf.keras.Sequential()
model.add(tf.keras.layers.SimpleRNN(units=middle_units, return_sequences=True, input_shape=(n_rnn, n_input)))
model.add(tf.keras.layers.Dense(n_out, activation='linear'))
model.compile(optimizer='sgd', loss='mean_squared_error')- summaryはこんな感じ。

Sequentialをひとまずインスタンス化して、今回は中間層からシーケンスが入力されるのと、リカレント(現在地的な感覚でいいです)のXの要素の複数出力があるので、.addメソッドを使います。
では、SimpleRNNのドキュメントを見ておきます。
tf.keras.layers.SimpleRNN(
units, activation='tanh', use_bias=True,
kernel_initializer='glorot_uniform',
recurrent_initializer='orthogonal',
bias_initializer='zeros', kernel_regularizer=None,
recurrent_regularizer=None, bias_regularizer=None, activity_regularizer=None,
kernel_constraint=None, recurrent_constraint=None, bias_constraint=None,
dropout=0.0, recurrent_dropout=0.0, return_sequences=False, return_state=False,
go_backwards=False, stateful=False, unroll=False, **kwargs
)
めちゃくちゃパラメータが多いので、かいつまんで。(以前のRNN入門でも少し説明した記憶があるので、そちらでもおけです)
return_sequences: 次の中間層への入力にシーケンスを返すには必ずTrueにする必要があります。
activation: デフォルトはtanh。(今回は恒等関数の'linear')
ちなみに、生成されたmodelのinputは[バッチサイズ, シーケンスの長さ, 特徴量の数]で指定する必要があります(そのためのX, tとかのreshapeでした。)
では、実際にfitして、どのくらい損失関数が小さくなっているのかプロットします。
history = model.fit(X, t, validation_split=0.1, batch_size=batch_size, epochs=num_epochs)
hist = history.history
loss = hist['loss']
val_loss = hist['val_loss']
plt.plot(loss, label='loss')
plt.plot(val_loss, label='val_loss', linestyle='--')
plt.legend()
plt.show()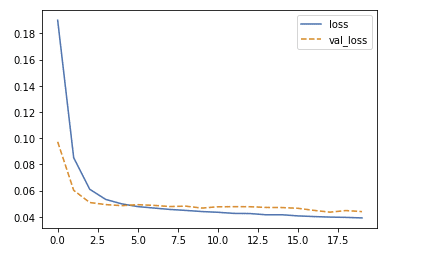
実際に学習データも検証データも訓練していくと下がっていくことが確認できました。
では、次にどのくらい予測できているのかを見て行きます。
# 初期値として最初の0を格納しておく
predicted = X[0].reshape(-1)
for i in range(0, n_samples):
y = model.predict(predicted[-n_rnn:].reshape(1, n_rnn, 1))
# print(y[0])
predicted = np.append(predicted, y[0][n_rnn-1][0])
plt.plot(y_data, label='Target')
plt.plot(predicted, label='Predict')
plt.legend()
plt.show()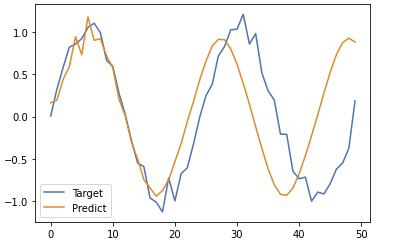
(自分がなぜy[0][n_rnn-1][0]のような値の取り方してるかわからなかったので、)ちょっと説明します。
まず、最初からn_rnn個までは満足に過去の情報を取得できないため、まずはpredictedという変数として格納しておきます。
で、for文で予測した値をpredicetedに格納していくのですが、ちょっと先に図を示してから説明に入ります。



ちょっとだけ文章の方でも補足します
なぜにpredictedにappendするのはy[0][n_rnn-1][0]なのかということですが、
X[i+1] = t[i] というXの一つ先の未来をtが値として保持しているわけで、
t[-1]番目のみxの次の値を予測していると言えるわけです。
つまり、predictで予測されるtの0~末尾一つ手前までは、Xの情報を予測しているだけであり、本当に予測した値として換算できるのは y[0][n_rnn-1][0]である、ということです。
(伝わってる自信はないです)
・(仮)SimpleRNNだけで文章生成
(↑の見れなかったら飛ばしてくださいw)
SimpleRNNでも文章予測ができるのですが、自分のコード理解が
かなりあやしいので、一旦参考までに留めておいてください。
(予測部分が読むの面倒ってのもあり、先に進めたいので。
ここらへんtensorflowの強さでもあるのですが、初心者殺しというか、良くも悪くも理解せずに進められてしまうのは結構のちのち響くのですねw)
・LSTM~導入~
さっくりと外観から。
RNNの入門やSimpleRNNの実装を見ても分かるように、SimpleRNNだけでは、長い文章においての文章保持能力(正確な用語ではないです)がありません。
つまり、記憶力(momery)が悪いわけです。
そこで対策としてLSTM(Long Short Term Memory)というものが研究されました(ちなみに、GRUは2014年くらいで最近のやつ。)
(理論もGRUと似ていたり、実装するだけしてみたいのであれば簡単ですが、使いこなせるようになるにはかなり時間かかりそうな気がしているLSTMです。)
その前に、RNNのおさらい。
SimpleRNNでは
y_t = h_t = tanh(x_t, h_{t-1}) = tanh(W_xh * x_t + W_hh * h_{t-1} + b)
(文章の表現の限界があるため、表記は正確でないです)
言葉で表現すると、
tが進んでいくと情報があちこち飛んでいってしまう、
ということになります。
ここでLSTMが出てきます。
====
ここから理論にいきます。
(順に説明しますが、興味ない方は飛ばしてください)
式を一気に表示した後、何が何をいっているのか?を説明することにします。
(今回はsigmoid関数とかtanhとか出てくるのですが、解説は割愛します。理論で出てくる頻度高いので、一度まとめて解説する回とか設けようかしら?とは思っていますが、余力があればのお話。。)

順番に見て行きます。
まずはc_tから。
式を見ると一つ前のc_(t-1)に f (のちに解説。forget gateとか忘却ゲートとか)がかけられて、
それとc' にi_tがかけられているものの和をとっています。
(表記上「'」としていますが、「~」のこと)
いや、これだけ聞いても・・ってなりますが、噛み砕いて行きます。
まずc_tは長期記憶を担当しているものと考えて行きます
(のちにcも解説。)
このf_tですが、fは入力x_tと過去の過去の記憶h_(t-1)をsigmoidにかけられています。(→つまり0~1の範囲に落ち着く)
例えば、f_t=1なら完全にc_(t-1)の記憶を保持してリカレント層のc_tに渡されます。つまり、前の記憶をばっちり覚えていることになります。
逆にf_t = 0なら過去の記憶を全捨てします。
感覚としてはf_tは「GATE(ゲート)」であるため、f=1なら全開放されたゲート、f=0なら完全に閉じられたゲート、みたいなイメージを持ってもらえればいいのかなと。

では、もう片方のi_t とc'を見て行きます。
c'をみてみるとリカレント層(いわゆる現在地点的な層。)への入力x_tと過去の記憶h_(t-1)をtanhでぎゅっとして出力されたものとなります。
どの程度今の入力と過去の記憶からどういう情報を長期記憶に残すの?って感じです。
では、i_tはc'のtanh -> sigmoidになったものになります。(ちなみにinput gate とか入力ゲートとか言われます。)
忘却ゲートと似たようにi_t = 1であれば長期記憶に完全に残そう!ってなり、=0なら全く残さない(文の変わり目のようなとき)ことになります。
つまり、
c_tにある二つの和のうち
前半では、前までの記憶のうちどのくらい残すのか?
後半は、入力されたものをどのくらいを覚えておくべきか?
ということを表しています。
(このcは context vectorとかいわれます)
残りの o, h をみます。
o_t(output gate とか出力ゲート)の関数をみると、他と似た感じですが、簡単に言えば長期記憶にいるものと短期記憶でいいものの度合いを0~1で表現しているもの、くらいでおけです。
推理小説とかで天気の文章とかよりも人の行動の叙述の方が重要度が高いときに、人の行動を示すような文章は長期的に残した方がいいわけです。
逆に、h_tは全て変数のように使われていることがポイントだったりします。
つまり、h_tとh_(t-1)に関係性がなく、長期的な役割を担わないことから
短期記憶的な役割を表していると言われたりしています。
ここまでが理論ですが、まとめると
長期と短期で記憶を分けて、「うまい具合に」次の時系列に渡す
これがLSTMとなります。
==理論終わり==
実際には有名な図とかあるのですが、GRUのときに書いて疲れたので、そちらを参照にww。
・さっくりと簡素なLSTMを実装
では、SimpleRNNと同じくsin curveでLSTMを使ってみます(次回以降でがっつりデータ使って構築してみます。)
とはいえ、ほとんどSimpleRNNの実装と似ていますので、サクサク行きます
では、データの準備から
np.random.seed(1)
x = np.linspace(-2 * np.pi, 2 * np.pi)
sin_data = np.sin(x) + 0.1 * np.random.randn(len(x))
plt.plot(sin_data)
plt.plot()
次にデータをkerasのlayersに入れるために処理して行きます(SimpleRNNの部分を参照)
今回のt(正解データ)に関してはXの最後の要素1つのみに絞ります。
# シーケンスの長さ(各自決めて良い)
lstm_seq_length = 10
# LSTMのユニット数
lstm_units = 20
# バッチサイズ
batch_size = 10
# エポック数
num_epochs = 300
# size
data_size = len(x)
# サンプルサイズ
n_samples = data_size - lstm_seq_length
X = np.zeros((n_samples, lstm_seq_length))
t = np.zeros((n_samples, ))
for i in range(n_samples):
X[i] = sin_data[i:i+lstm_seq_length]
t[i] = sin_data[i+lstm_seq_length]
# (batch_size, seq_length, features)に変形
X = X.reshape(n_samples, lstm_seq_length, 1)
t = t.reshape(n_samples, 1)ここから、モデルのコンパイルやらfitやら。
学習までの流れもほぼ一緒なので、LSTMのドキュメント等は最後にみます。
では、駆け抜けます!
model = tf.keras.Sequential()
model.add(tf.keras.layers.LSTM(lstm_seq_length, input_shape = (lstm_seq_length, 1)))
model.add(tf.keras.layers.Dense(1, activation='linear'))
model.compile(optimizer='sgd', loss='mean_squared_error')model.summary()
history = model.fit(X, t, batch_size=batch_size, epochs=num_epochs, verbose=0)loss = history.history['loss']
plt.plot(loss)
plt.title('LSTM Loss')
plt.show()
SimpleRNNにくらべ、学習が収束するまでに回数を要していることがわかります。
つまり、長期記憶を保持できるものの、学習には時間がかかるというわけですね。
では、予測してみます。
predictions = X[0].reshape(-1)
for _ in range(n_samples):
pred = model.predict(predictions[-lstm_seq_length:].reshape(1, lstm_seq_length, 1))
predictions = np.append(predictions, pred[0][0])
plt.plot(sin_data, label='Training Data')
plt.plot(predictions, label='Predicted Data')
plt.legend()
plt.show()
なんと!SimpleRNNよりも非常に近い形で予測していることがわかりますね。
SimpleRNNは長期になればなるほど予測がずれていましたが、さすがLSTMといったところでしょうか。
では、LSTMのドキュメントを見ておきます。
tf.keras.layers.LSTM(
units, activation='tanh', recurrent_activation='sigmoid',
use_bias=True, kernel_initializer='glorot_uniform',
recurrent_initializer='orthogonal',
bias_initializer='zeros', unit_forget_bias=True,
kernel_regularizer=None, recurrent_regularizer=None, bias_regularizer=None,
activity_regularizer=None, kernel_constraint=None, recurrent_constraint=None,
bias_constraint=None, dropout=0.0, recurrent_dropout=0.0,
return_sequences=False, return_state=False, go_backwards=False, stateful=False,
time_major=False, unroll=False, **kwargs
)
特に今ここで解説するものもちょっとない気がしたので、使う時に適宜補足することにします。。
どうせ実装するときにはいろいろパラメータ使うので。。(ため息ですな。。)
(自分がエポック数とかバッチサイズの決め方がわからなかったのですが、Qiitaでいい記事あったので、共有しておきます。
)
----
(おまけ)GRUはLSTMの層を.GRUにするだけです。
model_gru = tf.keras.Sequential()
model_gru.add(tf.keras.layers.GRU(lstm_seq_length, input_shape = (lstm_seq_length, 1)))
model_gru.add(tf.keras.layers.Dense(1, activation='linear'))
model_gru.compile(optimizer='sgd', loss='mean_squared_error')
history_gru = model_gru.fit(X, t, batch_size=batch_size, epochs=num_epochs, verbose=0)
loss = history_gru.history['loss']
plt.plot(loss)
plt.title('GRU Loss')
plt.show()
predictions = X[0].reshape(-1)
for _ in range(n_samples):
pred = model_gru.predict(predictions[-lstm_seq_length:].reshape(1, lstm_seq_length, 1))
predictions = np.append(predictions, pred[0][0])
plt.plot(sin_data, label='Training Data')
plt.plot(predictions, label='Predicted Data')
plt.legend()
plt.show()
・一旦終わり
LSTMの概要はこの辺にしておきます。
ここからちょっと本格的に構築したり、seq2seqでチャットbot作ったりできればと思います。
とはいえ、先ほども書きましたがこのへんは難しくなってきますね。。
ですが、tensorflowは理解せずともなんとなくパラメータ変えるだけで動いたり成果出たりします。なので実は理解が甘い人もいます(私です)
実装だけしたい!って方とかにはとても便利ですしね。。
ですが、ここではなるべく丁寧に少なくとも言語化できるくらいに理解して書いて行きます。。
・(不定期更新のおまけ)
(ほんとはtqdmにかんして書こうと思ったのですが、諸事情で変えました)
今回は標準モジュールであるglobです。
このglobとかosとかtimeは基礎を学ぶときにはそこまで学ばないけれど、実装するにあたり避けて通れなかったりするモジュールですね。
globに関しては、何かしらのファイルやパスをリスト形式で取得するものです。
では、簡単に使い方を見て行きますが、それにあたり以下のサイトからフリーデータをダウンロードして解凍しておきます(ちょっと重い)
globは標準で備わっているため、import globだけで動きます。
実際に試しに今のpathからどのようなファイルがあるのか確認してみます。

人によって結果は違うと思いますが、出力されました(わかりやすいようにjupyter labでファイルとかコードを同時に確認しています。)
では、ファイルの中身をみてみたい時は以下。

globの中のglobメソッドとあとはワイルドカード「*」で一気に閲覧しています。(いわゆる正規表現)
その他にも2階層下にあるもの全て取り出したいとき、5~9の数字がついたものだけを取得してみたい!って時は以下。

ま、こんなもんです。
個人的感想としては「使う時は使う」っていうくらいのモジュールで、今のtensorflowとかですぐすぐ必要というわけではないですw
しかし、実装とかでは結構見かけるので、簡単なおまけでした!
では、また次回〜
この記事が気に入ったらサポートをしてみませんか?
