CDSのプレミアムはなぜ100%を超えうるのか
CDSのプレミアムは、過去に100%を超えたことがあります(例えば、下記の記事です)。CDSのプレミアムが100%を超えた場合、プレミアムとして100%以上を貰えるのだから、絶対に得をしてしまうような印象をうけ、違和感があるという質問をうけました。たしかに、100%以上のプレミアムが得られるなら、元本がなくなっても問題ないように思われ、違和感があるということだとおもいます。その時のやり取りについて簡単なメモとして残しておきます。こちらも必要に応じてアップデイトします。
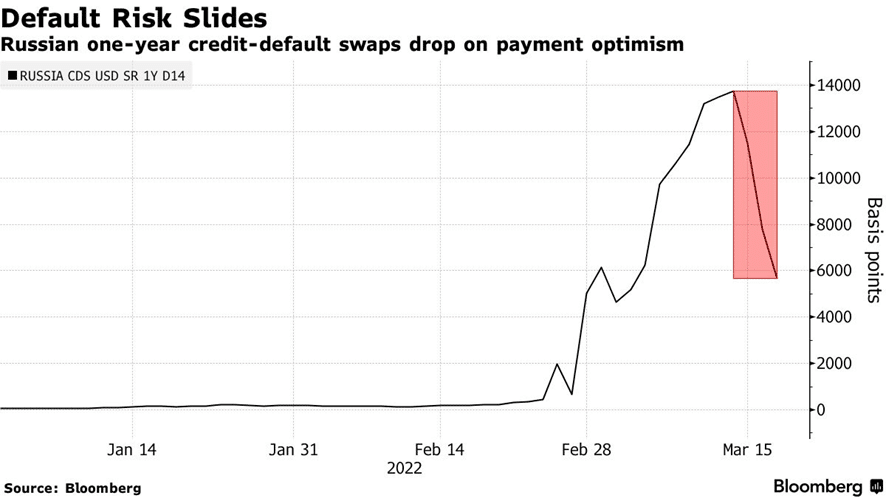
まず、この疑問は、おそらくCDSの商品性が複雑であることに起因するとおもいます。おそらく社債であればわかりやすいため、まずは社債で100%以上のリターンが起こることを考えます。ちなみに、社債とCDSは(デフォルトなどの定義が若干違うのですが)類似性が高くアービトラージがなされています。
まず、社債が100円で発行されたとして、その会社が破綻が見込まれる場合、その価格は大幅に低下します。社債については、破綻が見込まれるときは、破綻が起こった場合にどれくらいの残余財産が残るか等を投資家が予想してプライシングがなされますが、ここではほぼ破綻が予想され、若干残余財産が見込まれることから、1円の価格がついているとします。
利回りとは、最後まで持ち切ったときのリターン(Yield to maturity)なので、この社債を仮に満期まで持ち切れるとすれば、1円投資したものが100円になって返済されるため、投資額が100倍になり、9900%の利回りというイメージになります。このように考えれば、社債であれば、100%以上のリターンになりえることは明らかです。
CDSでも基本的に同じことが起こっています。そもそも、CDSとは、ある会社がデフォルトしたときの保険契約です。例えば、A社のデフォルトについて、私と読者で保険契約を結ぶとします。これはA社が仮にデフォルトした場合、その保証を受けられる保険です。ここでは私はその保険(プロテクション)を買う一方、読者はプロテクションを売るとしましょう。
そのうえで、仮にA社がほぼデフォルトすると見込まれているとします。A社がデフォルトしたら100円に対して0円も戻ってこないとします。私はプロテクションを買っているので、A社がデフォルトしたら読者から100円もらいます。読者から100円をもらえれば、A社がデフォルトしても100円返ってくるので、私にとって保険として機能します。
一方、読者からみれば、この保険を私に売っているので、私からその保険料を受け取ります。この場合、A社はデフォルトすることが見込まれているので、読者はそのプレミアムとして、100円に近い金額をもらいたいでしょう。ここで簡単化のため、99円のプレミアムで私と読者で合意したとします。
前述のとおり、利回りは「最後まで持ち切った場合の金利」(デフォルトが起こらないことが前提の金利)なので、読者からすれば、今99円もらって、デフォルトがおこらなければ0円の支払いというキャッシュフローは下記のようになります(これを(*)とします)。

このキャッシュフローを債券のように解釈できるようにするため、当初に100円払い、最後に100円の受け取る、というキャッシュフローを、(*)のキャッシュフローに加えます(ここではクレジットリスクを考えたいため、金利を捨象して、今の100と満期の100円の価値が同じと簡単化します)。そうすれば、(*)は下記のように、1円支払って、100円をもらうというキャッシュフローの価値と、(*)の価値は、同じであるといえます。

これは冒頭で説明した社債と同じキャッシュフローであることに気付いたとおもいますが、1円投資したものが100円になるため、投資額が100倍になるから、9900%の利回りというイメージになります。これがCDSのプレミアムが100%を超える直感です。
これを一般的にかくと、保険の売り手から見ると、保険料x円を貰って、デフォルトが起こらなければ0円の支払いというキャッシュ・フローとなりますが、これを債券仕立てにすると(100-x)円支払ってデフォルトが起こらなければ100円を貰う、よって100/(100-x)倍になる、利回りはx/(100-x)*100[%]=100x/(100-x)[%]となります。
このようにしてみれば、CDSのプレミアムが100%を超えないという誤解は、要はCDSスプレッドの定義を、分母が100-xではなく100であると誤解していた、ということが原因とも考えらえます。おそらく、ほとんどの場合、xが小さいと上のように誤解していても大差が生じないから、この点は気付きにくいのだと思います。しかしギリシャやロシアのように、xが100に近いくらい大きくなると誤解に伴う乖離が表面化してくるということです。
