財務省の不適切なデータ解析について

統計に明るくない方は下記URLを参照ください。

本投稿は、財務省主計局が公表した資料において、統計的な不備が存在するにもかかわらず結論を導いていると考えられる点を、事実ベースで指摘・説明するものです。
あくまでも事実に基づいた指摘を行っているものであり、陰謀論を助長する趣旨ではありません。根拠のない憶測や陰謀論には強く反対いたします。

1. はじめに

昨今、103万円の壁引き上げで財務省に対して 「積極財政をすべきだ」「緊縮財政をすべきだ」などの議論が盛んに行われています。

今回の問題の本質はそこではありません。
財務省主計局がIMFの一次データを用いて相関関係を分析する際に、 適切な統計処理を行わないまま結論を導いています。
積極財政・緊縮財政を語る以前の不適切な統計処理の問題です。

では、なぜその不適切な統計処理が問題になるのでしょうか。
それは、誤った処理によって可視化されたデータやグラフを使って議論しても、 妥当な結論を得ることができないからです。
適切な処理を施さなければ、 本来意味をもたない傾向や関係性が誤って示されることもあり、 積極財政や緊縮財政といった政策論争にすら正確な根拠を与えられません。

さらに、データの可視化は加工の仕方によっては、恣意的な二次データを見せたいように演出することすら可能です。

こうした問題を防ぐために、

• 厳密な統計処理

• なぜその解析を行ったのか

• どのような背景や仮説があったのか

• 統計的な有意性は検証されたのか

といった透明性のある検証プロセスが欠かせません。

統計に詳しくない方々は、「〇〇が言っているから間違っていないだろう」という判断で動きます。
これは統計的処理を厳密に行い、透明性を確保するから成り立つのです。

これはデータを取り扱う人間としての倫理観が問われいる重要な問題です。

これはデータを扱うすべての人間・組織において共通します。
文系・理系、あるいは出身学部は関係ありません。

2. 不適切な解析箇所

2024年11月29日に、財務省から「令和７年度予算の編成等に関する建議」を受け取りました。と投稿がありました。

本日、加藤大臣は、財政制度等審議会の十倉会長から「令和７年度予算の編成等に関する建議」を受け取りました。

詳細はこちら▼https://t.co/tmieaZ7LNC pic.twitter.com/EYlOMU6j2r

— 財務省 (@MOF_Japan) November 29, 2024

この「令和７年度予算の編成等に関する建議」には、統計的に不可解な点がいくつか見受けられます。本稿では、その中の一つについて取り上げ、財務省の統計解析上の問題点を事実に基づいて明らかにし、広く日本国民の皆様に知っていただきたいと考えています。

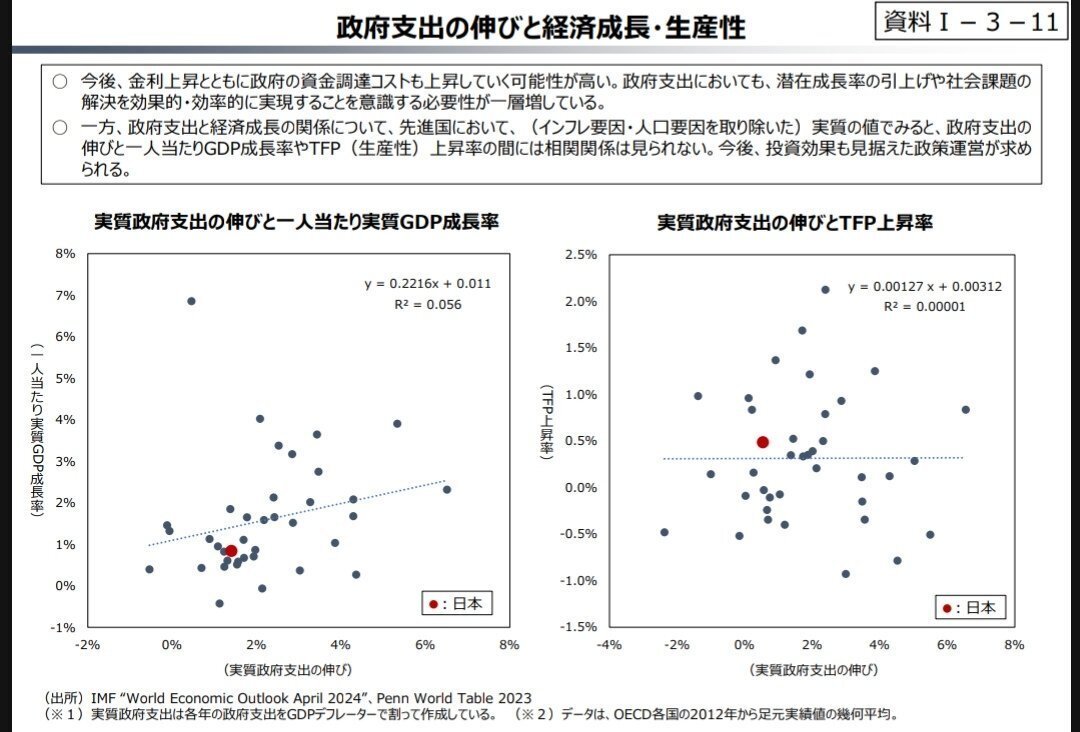
「令和７年度予算の編成等に関する建議」の12ページでは、GDP成長率と政府支出の関連について相関分析が示されています。本来、外れ値がある場合は、外れ値を除去してピアソン相関を用いるか、外れ値を含んだままスピアマン相関を用いるかといった選択肢を検討すべきです。

しかし、同建議のグラフでは、相関係数Rを求めるにあたって、そのままピアソン相関係数だけで分析を行った可能性が高いと推測されます。
さらに、相関を述べているにもかかわらず、回帰式を掲載している点も不可解です。相関の有無を議論したいのであれば、相関係数やその有意性（p値）を提示するほうが適切といえます。

図1 「令和７年度予算の編成等に関する建議」12ページ

図2 Y軸に明らかな外れ値がある(左図)

3. 当方(+その他のデータサイエンティスト)による解析

単に財務省主計局の解析を批判するだけでは、どうしても定性的な議論にとどまってしまいます。そこで当方や他のデータサイエンティストが実際にデータを解析し、定量的な根拠に基づく批判を展開いたします。

3-1. IMFの1次データを取得

IMF “World Economic Outlook (April, 2024)”のデータベースから抽出
Gross domestic product per capita, constant prices、General government total expenditure、Gross domestic product, deflatorより。

World Economic Outlook Database, October 2024

3-2. 散布図再現

Pythonを用いて財務省資料に沿って計算します。

id	Increase in government spending[%]	Increase of real GDP per person[%]
1	-0.313832285	0.314051684
2	-0.127508036	1.336649459
3	-0.024313068	1.235271761
4	0.483062194	6.92906856
5	0.781180992	0.412123689
6	0.983111888	1.016219914
7	1.188227813	1.008089097
8	1.342610762	-0.519763921
9	1.388884696	0.805221141
10	1.388884696	0.406926624
11	1.55227673	0.538606195
12	1.583808526	1.814866474
13	1.583808526	0.915145561
14	1.687003494	0.611450232
15	1.784465409	1.107806154
16	1.784465409	0.710225033
17	1.880207407	1.616940034
18	1.98066325	4.025813499
19	1.98066325	0.809878864
20	1.98066325	0.710305234
21	2.138385931	-0.018288617
22	2.185779175	1.515665728
23	2.174313068	1.938351032
24	2.288974144	3.313515509
25	2.489631027	3.109613316
26	2.644013976	1.38829179
27	2.978087212	0.429765276
28	3.239132262	1.986430956
29	3.389720475	3.517362202
30	3.389720475	2.618455708
31	3.94429788	0.981707473
32	4.186614955	1.90975813
33	4.17228232	1.435324484
34	4.186614955	0.311386426
35	5.287361286	3.817664534
36	6.284912648	2.321299427

上記計算結果を散布図にすると、当方と財務省の散布図がほぼ同じものとして再現できました。散布図自体は再現性があり。

図3 当方の散布図

図4 財務省の散布図

その他協力してくださったデータサイエンティスト2名(鶴は千年@Crane1000years様、hrk@GtgbSg様)もだいたい同じような散布図を再現しています。ほぼ同様の散布図が再現できました。

図5 鶴は千年(@Crane1000years)様による散布図再現

図6 hrk@GtgbSg様による再現

3-3. ピアソン相関と仮説検証

• 帰無仮説 (H0): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がない。」

• 対立仮説 (H1): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がある。」

上記をもとに計算を実施しました。

図7 ピアソン相関導出式

from scipy.stats import pearsonr

x = df["Increase in government spending[%]"]
y = df["Increase of real GDP per person[%]"]

pearson_corr, p_value = pearsonr(x, y)
pearson_corr, p_value

結果は

(0.19025026411347362, 0.26639419611413934)

• ピアソンの相関係数 (r): 0.190

• p値: 0.266

p値が0.05（一般的な有意水準）より大きいため、帰無仮説を棄却できません。つまり、統計的に有意な相関は見られませんでした。

図8 外れ値除去なしでのピアソン相関とp値

3-4. スピアマン相関と仮説検証

ピアソン相関は、外れ値に影響されやすいです。
スピアマン相関（順位相関）は外れ値の影響を受けにくく、データの単調な関係性を評価するため、ピアソン相関が有意でなかった場合でも、スピアマン相関では異なる結果が得られる可能性があります。
したがって、スピアマン相関でも相関分析を実施します。

図9 スピアマン相関導出式

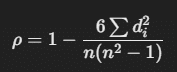
• 帰無仮説 (H0): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がない。」

• 対立仮説 (H1): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がある。」

from scipy.stats import spearmanr

spearman_corr, spearman_p_value = spearmanr(x, y)
spearman_corr, spearman_p_value

結果は

(0.37653731130589496, 0.023603516472017617)

• スピアマン相関係数 (ρ): 0.377

• p値: 0.024

p値が0.05（一般的な有意水準）より小さいため、帰無仮説を棄却します。つまり、政府支出の増加率と1人当たり実質GDPの増加率には統計的に有意な順位相関があると結論付けられます。

3-5. 途中考察

• ピアソン相関: 変数間の線形関係を評価します。外れ値に敏感であり、データが非線形な関係を持つ場合や、外れ値が存在する場合には相関が弱く出ることがあります。

• スピアマン相関: 変数間の単調関係（増加または減少する一貫した傾向）を評価します。外れ値の影響を受けにくく、順位情報に基づくため、非線形な関係にも対応します。

1. 外れ値の存在
   散布図を見ると、データの一部が他と離れている「外れ値」のように見える点があります。ピアソン相関はこれらの影響を受けやすく、全体的な線形関係を弱めている可能性があります。一方、スピアマン相関は順位に基づくため、外れ値の影響を受けにくい特性があります。

2. 非線形関係の可能性
   散布図を見る限り、政府支出の増加率と実質GDPの増加率の関係が単純な線形関係ではない可能性があります。スピアマン相関は単調な増加や減少を捉えるため、非線形の傾向が存在するとスピアマンで相関が現れることがあります。

3. データの分布の偏り
   ピアソン相関は正規分布に近いデータに適しており、非正規分布や歪んだデータでは相関が弱く出ることがあります。スピアマン相関はこの影響を受けにくいです。

よって次は、外れ値が本当に外れ値なのかを検証します。

3-6. 外れ値の検出

外れ値には様々な検出方法がありますが、IQR（四分位範囲）とロバスト統計（MAD法）の2種類を用います。

• IQR（四分位範囲）

q1_x = np.percentile(x, 25)  # 第1四分位数
q3_x = np.percentile(x, 75)  # 第3四分位数
iqr_x = q3_x - q1_x          # IQR
lower_bound_x = q1_x - 1.5 * iqr_x 
upper_bound_x = q3_x + 1.5 * iqr_x 

q1_y = np.percentile(y, 25)  # 第1四分位数
q3_y = np.percentile(y, 75)  # 第3四分位数
iqr_y = q3_y - q1_y          # IQR
lower_bound_y = q1_y - 1.5 * iqr_y 
upper_bound_y = q3_y + 1.5 * iqr_y 

outliers = df[
    (x < lower_bound_x) | (x > upper_bound_x) |
    (y < lower_bound_y) | (y > upper_bound_y)
]

df_no_outliers = df[
    (x >= lower_bound_x) & (x <= upper_bound_x) &
    (y >= lower_bound_y) & (y <= upper_bound_y)
]

外れ値はid=4, 18, 36でした。

id	Increase in government spending[%]	Increase of real GDP per person[%]
4	0.483062194	6.92906856
18	1.98066325	4.025813499
36	6.284912648	2.321299427

図10 箱ひげ図による可視化

• ロバスト統計（MAD法）

# MADスコア = |データ点 - 中央値| / MAD
outliers_mad_x["MAD Score (X)"] = np.abs(outliers_mad_x["Increase in government spending[%]"] - x_median) / mad_x
outliers_mad_y["MAD Score (Y)"] = np.abs(outliers_mad_y["Increase of real GDP per person[%]"] - y_median) / mad_y

most_outlier_x = outliers_mad_x.loc[outliers_mad_x["MAD Score (X)"].idxmax()]
most_outlier_y = outliers_mad_y.loc[outliers_mad_y["MAD Score (Y)"].idxmax()]

most_outlier_x, most_outlier_y

結果は下記の通り。外れ値はid=4, 36でした。

(id                                    36.000000
 Increase in government spending[%]     6.284913
 Increase of real GDP per person[%]     2.321299
 MAD Score (X)                          6.614782
 Name: 35, dtype: float64,
 id                                    4.000000
 Increase in government spending[%]    0.483062
 Increase of real GDP per person[%]    6.929069
 MAD Score (Y)                         8.334904
 Name: 3, dtype: float64)

次に外れ値を個別に除外して相関を計算し、結果を比較します。

3-7. 除外すべき外れ値はどれか？

outlier_ids = outliers["id"].tolist()

results = []

for outlier_id in outlier_ids:
    df_subset = df[df["id"] != outlier_id]
    x_subset = df_subset["Increase in government spending[%]"]
    y_subset = df_subset["Increase of real GDP per person[%]"]
    
    pearson_corr, _ = pearsonr(x_subset, y_subset)
    spearman_corr, _ = spearmanr(x_subset, y_subset)
    
    results.append({
        "Excluded Outlier ID": outlier_id,
        "Pearson Correlation": pearson_corr,
        "Spearman Correlation": spearman_corr
    })

df_no_outliers = df_no_outliers.reset_index(drop=True)
x_no_outliers = df_no_outliers["Increase in government spending[%]"]
y_no_outliers = df_no_outliers["Increase of real GDP per person[%]"]

pearson_all_excluded, _ = pearsonr(x_no_outliers, y_no_outliers)
spearman_all_excluded, _ = spearmanr(x_no_outliers, y_no_outliers)

results.append({
    "Excluded Outlier ID": "All",
    "Pearson Correlation": pearson_all_excluded,
    "Spearman Correlation": spearman_all_excluded
})

r_df = pd.DataFrame(results)
r_df

結果
  Excluded Outlier ID  Pearson Correlation  Spearman Correlation
0                   4             0.428832              0.479854
1                  18             0.207818              0.392042
2                  36             0.168051              0.345596
3                 All             0.468218              0.465140

下記仮説を行います。

• 帰無仮説 (H0): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がない。」

• 対立仮説 (H1): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がある。」

外れ値IDごとにピアソン相関とスピアマン相関の値が変化しており、外れ値が相関に影響を与えていることが分かります。
外れ値ID=4 を除外した場合、ピアソン相関が 0.429、スピアマン相関が 0.480 に上昇し、両者ともに関係性が強まりました。他の外れ値（ID=18, 36）を除外しても相関が若干増加するものの、外れ値ID=4の影響が最も大きいことが示唆されます。

外れ値を含む場合、ピアソン相関では有意な関係は見られませんでしたが、スピアマン相関では有意な関係が認められました。
外れ値を個別または全体で除外した場合、ピアソン相関とスピアマン相関の両方で関係性が強化され、統計的有意性の検討が可能になります。

外れ値ID=4の除外が、相関の改善に最も寄与していることが明らかです。このデータ点が全体の相関に悪影響を与えている可能性が高いです。

ちなみにID=4の該当国はアイルランドです。
アイルランドを外れ値として除外してもよいか、データの背景を抑えることにします。

図11 hrk@GtgbSg様による再現散布図

3-8. アイルランドは外れ値か？

アイルランドは外れ値として外れ値として適当かどうかを調査しました。調査を進めるうちに、データサイエンティストの鶴は千年@Crane1000yearsさんが、三菱UFJリサーチ&コンサルティングの記事で、興味深い資料を見つけました。

○重債務危機に喘いだ2010年代前半とは対照的に、2010年代後半のアイルランド経済は高成長軌道に返り咲いた。特に2015年には、米国の医薬品メーカーの本社移転によりR&D（研究開発）資産が急増した影響を受けて、実質GDPが26.3％増という異例の高成長を記録した。

○アイルランドはかつて「GIIPS」の１つに数えられた重債務国である。巨額の公的債務の返済が長年の課題であったが、2015年のGDP急増を受けて公的債務残高の対GDP比率は大幅に低下することになった。ただGDPの増加に比べると税収の伸びは少なく、財政指標の改善に関してはかなり割り引いて評価する必要がある。

○なお、確かに財政の持続可能性を評価する上で公的債務残高の対GDP比率は重要な指標であるが、この指標はGDP統計の内容次第でいくらでも変化してしまう。アイルランドの経験はレアケースとは言え、財政の持続可能性を評価する上で公的債務残高の対GDP比率は一つの参考指標に過ぎず、本来はより複合的な視野からの検討する必要があることを我々に問いかけている

発展モデルが曲がり角を迎えたアイルランド経済　～直接投資の環境悪化が重荷に～
2019/07/09　土田 陽介　調査レポート　海外マクロ経済

発展モデルが曲がり角を迎えたアイルランド経済　～直接投資の環境悪化が重荷に～ | 三菱UFJリサーチ&コンサルティング

つまり、アイルランドは下記のようにまとめられます。

• 「1人当たり実質GDPの増加率（6.93%）」は多国籍企業の移転など一時的な要因に基づいており、一般的な政府支出と経済成長の関係を歪める可能性があります。

• アイルランドは政府支出よりも直接投資に依存しており、他国と異なる経済モデルを持っており、政府支出の増加率とGDP成長率の相関分析において、他の国と異質なデータ点となりました。高成長は一時的なものであり、持続的な経済成長を反映していません。

• 他国のデータと一緒に解析する際、アイルランドのケースが全体の傾向を歪めるリスクがあります。

ゆえに、ID=4, アイルランドは外れ値として認識される。という結論に至ります。

3-9. 当方の解析のまとめ

# 1. ID 4 を除外したデータでの分析
df_exclude_4 = df[df["id"] != 4]
x_exclude_4 = df_exclude_4["Increase in government spending[%]"]
y_exclude_4 = df_exclude_4["Increase of real GDP per person[%]"]

pearson_exclude_4, p_value_pearson_exclude_4 = pearsonr(x_exclude_4, y_exclude_4)
spearman_exclude_4, p_value_spearman_exclude_4 = spearmanr(x_exclude_4, y_exclude_4)

# 2. ID 4 を含めたデータでの分析
pearson_include_4, p_value_pearson_include_4 = pearsonr(x, y)
spearman_include_4, p_value_spearman_include_4 = spearmanr(x, y)

results_comparison = pd.DataFrame({
    "Analysis": ["Exclude ID 4", "Include ID 4"],
    "Pearson Correlation": [pearson_exclude_4, pearson_include_4],
    "Pearson p-value": [p_value_pearson_exclude_4, p_value_pearson_include_4],
    "Spearman Correlation": [spearman_exclude_4, spearman_include_4],
    "Spearman p-value": [p_value_spearman_exclude_4, p_value_spearman_include_4]
})

結果
       Analysis  Pearson Correlation  Pearson p-value  Spearman Correlation  \
0  Exclude ID 4             0.428832         0.010158              0.479854   
1  Include ID 4             0.190250         0.266394              0.376537   

   Spearman p-value  
0          0.003534  
1          0.023604  

• 帰無仮説 (H0): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がない。」

• 対立仮説 (H1): 「政府支出の増加率と1人当たり実質GDPの増加率には相関がある。」

ID=4 を除外した場合
ピアソン相関 (r): 0.429, p値: 0.010
スピアマン相関 (ρ): 0.480, p値: 0.004

ピアソン相関とスピアマン相関の両方で、p値が0.05より小さいため、帰無仮説を棄却します。
したがって、ID=4 を除外した場合、政府支出の増加率と1人当たり実質GDPの増加率の間に統計的に有意な相関が存在します。

ID 4 を含めた場合
ピアソン相関 (r): 0.190, p値: 0.266
スピアマン相関 (ρ): 0.377, p値: 0.024

ピアソン相関では、p値が0.05より大きいため、帰無仮説を棄却できません。
スピアマン相関では、p値が0.05より小さいため、帰無仮説を棄却します。
したがって、ID=4 を含めた場合、政府支出の増加率と1人当たり実質GDPの増加率の間に統計的に有意な単調相関が存在しますが、線形相関は統計的に有意ではありません。

• ID=4 を含めると、特異なケース（アイルランドの異常なGDP増加）によりピアソン相関が弱まり、統計的に有意な結果を得られません。

• ID=4 を除外すると、相関が統計的に有意となり、政府支出の増加率と1人当たり実質GDPの増加率に一定の関係性が認められます。

ここではじめて、重回帰分析やベイズ解析に移行できると考えます。
重回帰分析やベイズ解析といった解析や、財務省の他解析についてもご指摘されております。

学生時代に科研費研究や医療データの解析を行っていた程度ですが、問題点がいくつも見えます。

本来であれば、重回帰分析、パネルデータ分析を重ねる事で慎重に結論を導き出すべき問題と思います。

＜問題概要＞
・他の重要な経済変数をコントロールしていない…

— Gita (@nosce_te_ipsum2) December 27, 2024

4. 質問と財務省の回答

財務省主計局の質問にあたっては、浜田聡事務所の秘書である村上ゆかり（@yukarimurakami5）様を通じて行いました。村上様に深く感謝を申し上げます。

4-1-1. 質問1

明らかな外れ値が存在する場合にスピアマン相関係数（順位相関係数）ではなく、ピアソン相関係数を採用した理由は何でしょうか。

4-1-2. 財務省回答1

スピアマン相関係数は、主に序数や順位データによく用いられるノンパラメトリック手法であり、ピアソン相関係数は最も一般的な相関係数であると承知している。

4-1-3. 当方の見解1

スピアマン相関係数は実数データでも外れ値や非線形関係がある場合にロバストな手法として一般的に用いられますが、財務省回答は「一般的にピアソン相関を使った」という説明にとどまり、なぜ外れ値処理を行わずピアソン相関係数だけを用いたのか、当方の提示した「外れ値除去後の有意な相関」についても言及がなく、不十分です。

4-2-1. 質問2

 資料I-3-11のグラフにおいて、明らかな外れ値として見える国名はどこですか。

4-2-2. 財務省回答2

本グラフにおける左上のマーカーはアイルランドである。

4-2-3. 当方の見解2

当方のデータ検証でも、ほかデータサイエンティストの散布図でも一致しており、ここについては問題ありません。

4-3-1. 質問3

データ算出にあたり、IMF World Economic Outlook (April 2024) および Penn World Tableのどのデータカラムを用いましたか。

4-3-2. 財務省回答3

IMF “World Economic Outlook (April, 2024)”のGross domestic product per capita, constant prices、General government total expenditure、Gross domestic product, deflatorを用いている。

4-3-3. 当方の見解3

当方側でも類似のプロットがほぼ再現可能であることを確認しており、回答は妥当です。

4-4-1. 質問4

「政府支出の伸び」と「1人当たりGDP成長率」に相関があるとする仮説検定の算出過程・結果（有意水準、検定統計量等）はどうなっていますか。

4-4-2. 財務省回答5

仮説検定は行っていない。

4-4-3. 当方の見解5

仮説検定を行わずに「相関がない」と結論づけるのは厳密性に欠けます。
統計的に不適切であり、非常に問題です。

4-5-1. 質問5

当方による試算では、外れ値除去後にピアソン相関（R=0.429, p=0.010）や外れ値を含めたスピアマン相関（ρ=0.377, p=0.024）で有意な相関が得られました。にもかかわらず最終的に「相関がない」と結論したのはなぜですか。

4-5-2. 財務省の回答5

ご指摘の資料に掲載したグラフは各国比較のための機械的な計算であり、特定の国を外れ値と定義し恣意的な処理を施さないようにした。したがって『相関が見られない』と記述した。

4-5-3. 当方の見解5

外れ値を考慮せずに結論を出すことは統計的に頑健性を欠きます。
外れ値処理を「恣意的」とみなすのではなく、むしろ統計手法として外れ値を適切に処理するのは一般的な実務です。
財務省は当方が示した有意な相関結果について言及がなく、回答は不十分です。

4-6-1. 質問6

相関係数ではなく回帰分析（単回帰）と決定係数を示した意図は何ですか。

4-6-2. 財務省回答6

本グラフでは単回帰分析を行っており、決定係数（R^2）を1/2乗したものが相関係数（R）に相当する。

4-6-3. 当方の見解6

当方は教科書レベルのことを、わざわざ財務省に聞いているのではありません。
回帰分析（単回帰）と決定係数を示した意図に対する質問に答えていません。
相関の有無を議論する際にはピアソン・スピアマンの相関係数やp値を提示した方が明確かつ適切です。

4-7-1. 質問7

本試算は財務省自身が行ったものか、それとも外部機関または他省庁によるものですか。

4-7-2. 財務省回答7

財務省主計局が行ったものである。

4-7-3. 当方の見解7

財務省をはじめとする中央省庁には、データアナリストが存在します。
統計データアナリストが5人、統計データアナリスト補が11人です。

中央省庁全体では、統計データアナリストが下記人数存在します。
人事3
内閣府3
総務16
財務5
文科2
厚労5
農水7
経産17
国交8

統計データアナリストが5人、統計データアナリスト補が11人も存在する財務省で、不適切な統計処理を用いて結論付けたことは、甚だ疑問です。

二　政府職員のうち、統計検定以外で、統計に関する専門知識を有している事が示される国家資格または資格を有している職員がいれば、資格の種類とその人数をそれぞれの省庁ごとに示されたい。

二について
　お尋ねの「統計に関する専門知識を有している事が示される国家資格または資格を有している職員」の意味するところが必ずしも明らかではないが、例えば、総務省政策統括官（統計制度担当）が各府省の職員の実務経験及び受講した研修の内容を踏まえて認定する「統計データアナリスト」及び「統計データアナリスト補」について、認定を開始した令和三年度から令和五年度末までに認定した延べ人数を認定時点の所属府省ごとにお示しすると、「統計データアナリスト」は、人事院三人、内閣府三人、総務省十六人、財務省五人、文部科学省二人、厚生労働省五人、農林水産省七人、経済産業省十七人及び国土交通省八人であり、「統計データアナリスト補」は、人事院五人、内閣府十九人、総務省百六十五人、財務省十一人、文部科学省五人、厚生労働省三十一人、農林水産省三十一人、経済産業省十六人及び国土交通省十一人である。

令和6年5月21日
岸田内閣が推し進めるＥＢＰＭを実践する上で必要不可欠である政府職員の統計に関する専門性に関する質問主意書
提出回次213回　提出番号130
提出日令和6年5月9日
浜田聡君
https://www.sangiin.go.jp/japanese/joho1/kousei/syuisyo/213/meisai/m213130.htm

下記が財務省とのやり取りです。

財務省主計局より回答が来ました。

【回答】
１．スピアマン相関係数は、主に序数や順位データによく用いられるノンパラメトリック・テストの一つであり、ピアソン相関係数は、多くの定義がある相関係数の中で最もよく用いられるものと承知している。… https://t.co/VGmbFTxfdS

— 村上ゆかり (@yukarimurakami5) December 16, 2024

5. 追加質問と再回答

当方からさらに追加で以下の質問を行いました（外れ値処理や仮説検定などを再度詳細に質問）。
しかし、財務省からは下記回答のみで、個々の追加質問に対して具体的な返答は示されませんでした。

5-1. 追加質問

1. 外れ値処理の明確化（標準的外れ値判定手法やロバスト推定法の検討は行われましたか、有意な相関結果をどう評価・考慮しましたか？）

2. 相関解析における有意性検定を行わずに「相関がない」と結論した理由は何ですか？

3. 外れ値へのロバストな統計手法（スピアマン相関、ロバスト回帰等）の検討・試行状況をご教示ください。

4. 信頼区間や標準誤差、p値など不確実性情報の提示を行いましたか？

5. 外れ値国（アイルランド）を含めたデータ特性の検証や外れ値診断手法（Cookの距離、DFBETAS等）の実施状況をご教示ください。実施があればその理由も示してください。なければその理由もご教示願います。

5-2. 財務省からの再回答

以前ご回答を差し上げたとおり、経済データを観察・分析する際には様々な手法や結果の解釈があると承知しているが、当該資料のグラフはＯＥＣＤ各国比較のための機械的な計算で、『相関関係が見られない』としたものである。

5-3. 当方の見解

個別の追加質問に対して具体的な応答はなく、「機械的な計算」という理由のみが繰り返されています。
追加質問への直接的・十分な回答は「得られていない」と判断しました。

7.でも記述していますが「機械的な計算」を用いて結論を導き出してはいけません。

下記が財務省との再質問のやり取りです。

財務省主税局より今しがた回答が来ました。

ーーーーーー…

— 村上ゆかり (@yukarimurakami5) December 27, 2024

6. まとめ

当方および協力していただいたデータサイエンティストの方々は、IMFの一次データを基に財務省が示した散布図をほぼ再現し、さらに独自で解析を行い財務省の解析手法の矛盾点を指摘しました。

そして「令和７年度予算の編成等に関する建議」12ページに掲載された内容について「不適切ではないか」と質問を行いましたが、残念ながら具体的な回答は得られませんでした。

ご説明を頂けなかった点は大変残念であり、誠に遺憾に存じます。

7. さいごに

私は減税派でも増税派でもありません（もちろん減税になれば嬉しいですが、必ずしも減税がすべて正解とは思っていません）。
ただの一人のデータサイエンティストです。

私は、国家の将来を左右する中央省庁がデータに基づいて意思決定を行う際には、適切にデータを処理し、なぜその解析に至ったかを国民に対して広く説明する責任があると考えています。
なぜなら、一次データから二次データへの加工や可視化は、そのやり方次第でいくらでも“誤解を誘うような操作”が可能だからです。
そうした事態を避けるためにも、厳密な統計的処理と、背景や理論の開示が不可欠だと思います。

統計に詳しくない方々は「財務省が言っているのだから間違いないだろう」と判断しがちですが、これは統計的処理を厳密に行い、透明性を確保してはじめて成り立つものです。

これは、データを取り扱う人間としての倫理観が問われる、極めて重要な問題です。
ただ機械的に統計処理した結果だけを示して断定するのは、上記の理由から避けるべきだと思います。

今回の財務省の一連の解析と回答は、不誠実極まりないものでした。
このような対応が続く限り、財務省が提示するデータの信頼性は低いままになってしまうでしょう。

巷では「財務省が恣意的にデータをつぎはぎしている」という“財務省陰謀論”すら取り沙汰されています。
私はそのような陰謀論は否定していますが、残念ながら、今回の財務省の回答からはそうした論を払拭するだけの材料が得られませんでした。

8. 謝辞

今回の解析にあたりデータサイエンティスト(鶴は千年@Crane1000years様、hrk@GtgbSg様)には多大なご助力をいただきました。ここに厚く御礼申し上げます。

また財務省主計局の質問にあたっては、NHK党の浜田聡(@satoshi_hamada)参議院議員および浜田聡事務所の秘書である村上ゆかり（@yukarimurakami5）様を通じてご尽力いただきましたことを、心より感謝申し上げます。