許容下落率と保証金維持率から最大レバレッジを算出したい（信用取引編）【全文無料】

備忘録を兼ねたメモ用。計算ミス等あればご指摘ください。
（全文無料範囲です。良かったら投げ銭ください）
※2024-04-22：盛大に計算ミスをやらかしていたので、全面改訂しました。

やりたいこと

マルチアセットでのアセットアロケーションを選定した場合を考える。その資産のうちの一部にレバレッジをかけて運用することで、ポートフォリオ全体にレバレッジを掛けたような状態にしたい。

トービンの分離定理　現代ポートフォリオ理論の概念の一つ。最適なポートフォリオを決定するにあたって、投資家のポートフォリオの選択問題が以下のように２つの問題に分離される。
　1）リターン＆リスクの関係から「接点ポートフォリオ」を決定する（CAPMなど）
　2）リスク許容度に応じて、接点ポートフォリオと安全資産の配分比率を決定する
一般に、投資家の効用や選好は接点ポートフォリオの構成比率とは無関係で、接点ポートフォリオと安全資産の配分比率に関してのみ選好に応じて決定する。リスク選好度が高ければ無リスク資産を持たないか、またはレバレッジをかけることによってリターンを底上げする。

レバレッジをかける方法としては、先物取引、信用取引、CFD、レバレッジETFなどが候補として挙げられるが、ここでは信用取引を選択する。信用取引のメリットは以下が挙げられる。

• トービンの分離定理を適用できる（レバレッジETFだとロスカットがないが、日次リバランスのため本来のアセットとは異なるリターン&リスクとなってしまう）

• 株式と損益通算できる（先物やCFDだとできない）

• 別アセットを代用有価証券として利用できる（信用二階建てはリスキーだが、少ない保証金で取引できる）

• 比較的変動の小さい米国債券なども上場ETFを用いてレバレッジできる。

課題設定

以下のようなシチュエーションを設定する。ただし、金利や諸費用等は無視する。

シチュエーションの概念図

• あるアセットXを$${ \alpha(0<\alpha<1) }$$の割合で保有するようなリスク資産ポートフォリオを考える。

• 上記ポートフォリオのうち、アセットXの一部を信用取引することで、ポートフォリオ全体のレバレッジが$${ L(L>1 )}$$になるようにしたい。

• 委託保証金率は30%以上とする。信用取引でのレバレッジ$${ k }$$は$${ k \leq 1/0.3=3.33… }$$となる。

• 制約条件として、許容できる下落率$${ d(0 < d < 1) }$$であっても、保証金維持率$${ g(=0.2) }$$を満たすようにする。

• その際、ポートフォリオ全体のうち$${ s( 0< s<1) }$$の割合で持つ資産を、代用有価証券に適用する。

• 代用有価証券の掛率は$${ c(=0.8) }$$とし、代用有価証券に対しても上記の許容下落率を適用するものとする。

• ポートフォリオ全体のうち$${ t(0 < t < \alpha) }$$の割合で持つ資産を、非課税口座で運用されるアセットXの一部とする。（したがって、この割合$${ t }$$分の資産はアセットXの信用取引用の保証金に配分することができない）

アセットXのうち、ポートフォリオ全体に対しての信用取引の保証金割合を$${ x(0 \leq x \leq \alpha-t) }$$としたとき、取り得る最大の$${ L }$$とそのときの$${ x }$$を$${ d }$$で表したい。

導出

考え方は下記を参考とした。

2階建て信用取引でどのくらい建玉を建てていいか計算する - Qiita

証拠金と信用取引による増加分の関係から

$$
(k-1)(x+sc) = L - 1 \\
\\
\iff L = (k-1)(x+sc)+1　…①
$$

資金元本の関係から

$$
x + s + t = 1　…②
$$

保証金維持率の条件から

$$
g \leq \frac{ x + (1-d)sc - d (x ＋ sc) k }{ (x + sc) k } \\
 \\
\iff k \leq \frac{ x + (1-d)sc }{ (g+d) (x+sc) }　…③
$$

①～③より

$$
L \leq \frac{ (1-c)(1-g-d)+cd }{ g+d }  x + \frac{ 1-2d-g }{ g+d }  c(1-t) +1
$$

$${g=0.2}$$ であるから $${ d < 0.8}$$ の範囲において、$${L}$$は$${x}$$に対して単調増加となる。したがって、$${x}$$が最大のときに$${L}$$が最大となる。また、$${x=0}$$において$${L \geq 1}$$となる条件として$${1-2d-g>0}$$、つまり$${d<\frac{1-g}{2}=0.4}$$が存在することが分かる。

$${x}$$の条件から、$${x}$$の取り得る最大は

$$
x \leq \alpha -t 
$$

そのときの$${L}$$の最大値は

$$
L \leq \frac{ -\{ (\alpha-t) + 2c (1-t) \}  d + (1-g) \{ (\alpha-t) + c (1-a) \}  }{ g + d } + 1
$$

ここで、

$$
f(z) = \frac{ -Az+B }{ z+g }+1 \\
 \\
A=(\alpha-t)+2c(1-\alpha)　(>0) \\
B=(\alpha-t)+c(1-\alpha)　(>0)
$$

とおくと、

$$
\frac{df}{dz} = \frac{-Ag-B}{(z+g)^2} <0
$$

$${f}$$は$${z}$$に対して単調減少であることから、$${L}$$は$${d}$$に対して単調減少となる。これは許容下落率が小さいほどレバレッジを大きく取れることを意味する。

つまり、

$$
L_{\max} = \frac{ -Ad+B }{ d+g }+1 \\
 \\
A=(\alpha-t)+2c(1-\alpha) 、B=(\alpha-t)+c(1-\alpha) \\
 \\
x_{\max} = \alpha-t　、　k_{\max} = \frac{L_{\max}-1}{(1-c)x_{\max}+c(1-t)}+1 \\
 \\
なお、\alpha、g、t、cは既知であり、dは変数として考える
$$

となる

これにより、ポートフォリオのレバレッジ$${ L }$$の取り得る最大値$${L_{max}}$$と、その際に満たすべき信用取引の保証金と建玉を、許容下落率$${ d }$$の関数として表すことができる。

具体例

以下のケースを考える。

• アセットXの保有割合 $${ \alpha = 0.75 }$$

• 保証金維持率 $${ g=0.2 }$$

• 非課税口座の資産割合 $${ t=0.16 }$$

• 代用有価証券にできる資産割合 $${ s=0.2 }$$

• 代用有価証券の掛率 $${ c=0.8 }$$

想定下落率$${ d=0.4 }$$とすると、

• 信用取引の保証金割合 $${ x=0.59 }$$

• 信用取引のレバレッジ $${ k=1.50 }$$

• ポートフォリオ全体の最大レバレッジ $${ L=1.39 }$$

CFD取引の場合と比較して、最大レバレッジは大きくなっている。
（ここで$${\alpha}$$をCFD取引の場合に対して大きくしているのは、アセットXに対して債券等の株式以外の別アセットも含めることができるためである）

想定下落率$${d}$$に対する感度を信用取引とCFD取引で比較すると以下のようになる。

• 信用取引におけるアセットXの保有割合 $${ \alpha_{信用} = 0.75 }$$、
  CFD取引における保有割合$${\alpha_{CFD} = 0.5}$$

• 信用取引における保証金維持率を $${ g=0.2 }$$、
  CFD取引における取引金額に対する必要証拠金の割合を $${ g=0.1 }$$

• 代用有価証券にできる資産割合 $${ s=0.2 }$$

• 代用有価証券の掛率 $${ c=0.8 }$$

• 非課税口座の資産割合 $${ t=0.16 }$$

として、想定下落率$${ d }$$を$${ 0.1 \leq d \leq 0.6}$$の範囲で動かすと次のようになる。想定下落率が小さい場合は信用取引のほうが最大レバレッジが大きくなる。一方で、信用取引のほうが想定下落率に対する感度が大きいと言える。

横軸にd、縦軸Lをとったグラフ
信用取引の場合とCFD取引の場合でdに対する感度が異なる。

また、これらは保有割合$${\alpha}$$に対しても影響を受ける。保有割合$${\alpha}$$を$${ 0.2\leq \alpha \leq 0.8}$$の範囲で動かすと次のようになる。それぞれについて想定下落率$${d}$$を$${d=0.3、0.4、0.5}$$としたときで表示している。

いずれもの場合も$${\alpha}$$が大きいほうが$${L}$$は大きくすることができる。信用取引によって$${\alpha}$$を増やせる場合、軌跡としては左にシフトするためCFD取引よりも有利となる。

横軸にα、縦軸Lをとったグラフ
信用取引の場合とCFD取引の場合でαとdに対する感度が異なる。

例えば、株式の保有割合$${\alpha_{stock} = 0.5}$$、債券の保有割合$${\alpha_{treasury} = 0.25}$$で考える。信用取引では株式と債券を、CFD取引では株式のみを取引対象にできる場合、各$${\alpha}$$は以下のようになる。

$$
\alpha_{信用} = \alpha_{stock}+\alpha_{treasury} = 0.75 \\
\alpha_{CFD} = \alpha_{stock} = 0.5
$$

これは信用取引の軌跡を左に$${\alpha_{treasury}=0.25}$$シフトさせることを意味するので$${\alpha_{stock}=0.5}$$で比較すると以下のようになる。この場合、想定下落率が$${d\leq0.5}$$であれば信用取引のほうが有利であると言える。

横軸にα_stock、縦軸Lをとったグラフ
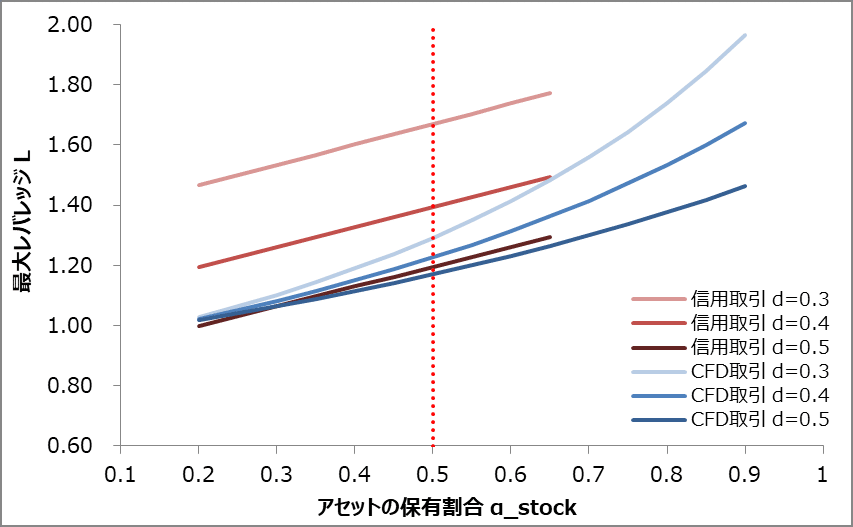
株式0.5、債券0.25の保有割合とした場合で比較