
統計学|検出力とはなんぞや
検出力の手計算がいつもぱっとできないので、これを機に検出力についてまとめてみようと思います。同時にこれから勉強したい、今そこ勉強中だよという方の参考になるとうれしいです 🌱
統計的仮説検定の基本的な流れ
最初に基本的な統計的仮説検定の流れを確認します。
1. 帰無仮説(H0)を設定する(例: μ = 0)
2. 対立仮説(H1)を設定する (例: μ = 1, μ > 0)
3. 有意水準(α)を決定する(例: α = 0.05)
4. サンプルから検定統計量を計算する
5. 4で計算した検定統計量が、3で決めた有意水準から求められる棄却域内に収まれば、H0 を棄却する
第1種の誤りと第2種の誤り
検定を行うときは有意水準・棄却域を定め、求めた検定統計量がその中に入ると自動的に H0 が棄却されます。しかし棄却域に入っているものの本当は H0 が正しい場合もあります。反対に本当は H1 が正しいのに棄却域に入らないことも考えられますね。
そういった仮説検定を行う際に起こりえる誤りについて確認しておきます。
ここでは例えば以下のように帰無仮説・対立仮説を設定しました。
H0 (帰無仮説) : μ = μ0
H1 (対立仮説) : μ = μ1

第1種の誤り(αエラー):H0 (μ = μ0) が正しいのに棄却してしまう確率
第2種の誤り(βエラー):H1 (μ = μ1) が正しいのに H0 を棄却できない確率
真の μ は μ0 なのに誤って H0 を棄却してしまうのがオレンジの部分の 第1種の誤り(αエラー)です。逆に、真の μ が μ1 だったとき誤って H0 を採択してしまうのが緑の部分の 第2種の誤り(βエラー)です。
仮説検定を行うときにそれらの誤りがどの程度起きるのか、また H0 が間違っている際どれだけ正しく H0 を棄却できるのか 知っておくことは大切そうですね。
検出力とは
第1種の誤りと第2種の誤りというものがあることは理解しました。ではこの記事のメインテーマ「検出力」とはなんなのかを見ていきたいと思います。

検出力 = 1 - βエラー
つまり検出力とは、H1 が正しいときに正しく H0 を棄却し、H1 を採択する確率です。
なぜ検出力を知りたいのか?
サインアップのボタンの色を青から赤に変えたときクリック率に有意な差があるかという検定をするとします。
H0: 青と赤で差はない(μ = μ0 = 0)
H1: 赤のほうが 3% クリック率が高い (μ = μ1 = 0.03)
※ 一般的には H1: μ > μ0 のように対立仮説が1点ではない場合が多いです。その場合は対立仮説に当てはまるすべての μ1 で検出力を考えます。
例えば、H0 と H1 の分布が以下のようになるとします。

図を見ると検出力が 5割 もありません。つまり 3% クリック率が上がっていたとしても正しく H1 を採択できる確率が低いことになります。もしあなたが最低でも 3% クリック率が上がっていたらボタンを赤にしたいと考えているのなら、この検定結果で判断するのはマズそうです。
このように仮説検定したものの実は検出力が低く正しく H0 を棄却できない、ということがないよう検出力がどれくらいなのか事前に知っておけるとよいですね。
検出力が高くなるのはどういう場合なのかと合わせて見ていきたいと思います。
検出力が高くなるとき1 - サンプルサイズが大きい場合
サンプルサイズが大きくなることで分散が小さくなり、その結果検出力が高くなります。

✐ 実際計算してみる
サンプルサイズが 5 個のときと、10 個のときで Z 検定を行う際、検出力がどうなるかを比較してみることにします。
その他の条件
・ 母集団 ND(μ, 1) からサンプリング
・ H0:μ = 0、 H1:μ = 1
・ 有意水準は片側 5 %
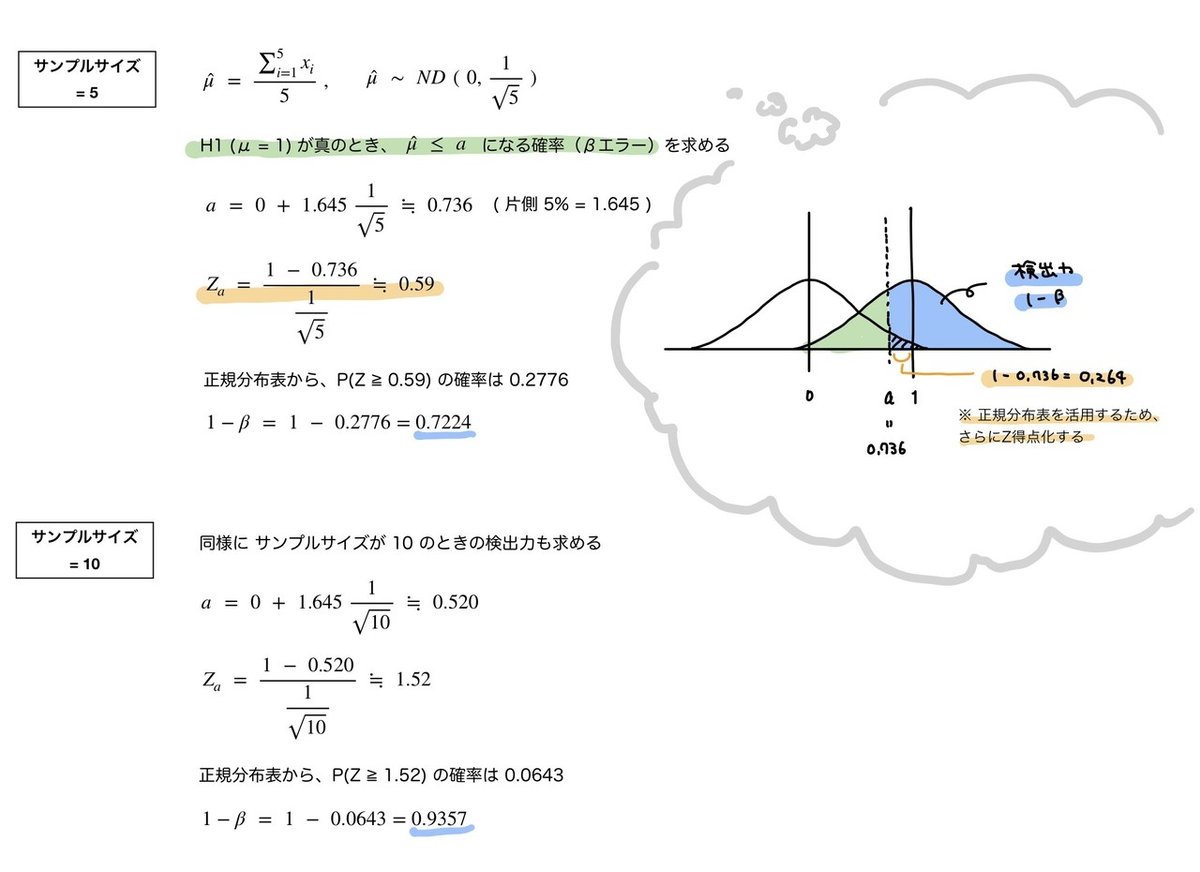
サンプルサイズ 10 の方が、5 のときより検出力が高くなっているのが確認できます。つまりサンプルサイズが大きいほうが検出力が高まります。
検出力が高くなるとき2 - H0 と H1 の差が大きいと想定する場合
H0 と H1 の μ(平均)の差を大きくすると検出力が高くなります。

H0 と H1 の μ の差を大きくしていったとき、検出力がどう変化するか R でプロットしてみます。今回サンプルサイズは 50、分散は 1 に固定します。
# 平均の差 0 ~ 1
deltas <- seq(0, 1, length=11)
# 分散 1、サンプルサイズ 50 の検出力
powers <- power.t.test(n=50, delta=deltas, sd=1)$power
plot(deltas, powers, type="l", xlab = "平均の差", ylab = "検出力")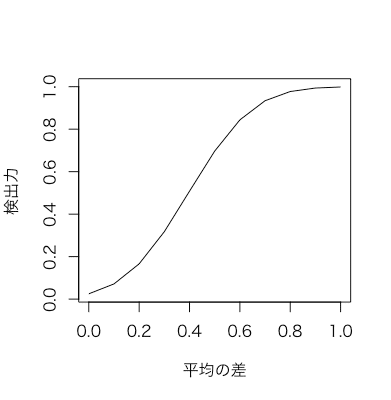
H0 と H1 の μ の差を大きくしていくと、検出力が上がっていくのがわかります。今回の条件では μ の差が 0.6 以上であれば 検出力 0.8 で検定できそうです。自分が望む検出力だとどのくらいの μ の差を判別できるか検定前に知っておくとよいと思います。
検出力が高くなるとき3 - 有意水準(α)が大きい場合
有意水準(αエラーを起こす確率)を引き上げると、検出力が大きくなります。

✐ 実際計算してみる
有意水準を片側 5 % と 片側 10 % にしたときの検出力を比較してみます。
その他の条件
・母集団 ND(μ, 1) から 5 つサンプリング
・ H0:μ = 0、 H1:μ = 1

計算の結果から、仮説検定を行った際 α エラーを起こす確率が大きいほうが検定力が高いことがわかります。
--- ✐ --- ✐ --- ✐ ---
今回はそもそも検出力がどういうものか、どういうときに大きくなるかについて考えました。これで以前よりはスラスラ問題が解ける...はず!
新しく勉強したいことも復習したいこともたくさんあるので、少しずつでも note にまとめていければと思います( *ˆoˆ* )
参考資料
統計の本、もしくはわんこにおいしいお菓子を買うのに使わせていただきます( *ˆoˆ* )
