
【考察】エビワラーじゃんけんにおける最強戦略を計算した話【ゲーム理論】
TL;DR
エビワラーじゃんけんの1ターン目における「混合戦略のナッシュ均衡」は:
マッハパンチ: 60.6%
はやてがえし: 17.7%
きあいパンチ: 21.7%
「混合戦略のナッシュ均衡」に従ってわざ選択を行うことで任意の相手に対して勝率を50%以上にすることができます。
エビワラーじゃんけん
皆さんはエビワラーじゃんけんをご存知でしょうか。
ポケモンSVに登場するエビワラーは次の三種のわざを覚えます:
・マッハパンチ
・はやてがえし
・きあいパンチ
実はこれらのわざは三すくみの関係になっており、これらでじゃんけんのような遊びをすることができます。この関係性を元にこの三種のわざだけをエビワラーに覚えさせてポケモン対戦をするというのが「エビワラーじゃんけん」です。考えた方は天才ですね。
わざの説明と相性
上のリンクに詳細な説明がありますが、以下にざっくりとしたわざの説明を書きます。ご存知の方は飛ばしてください。
マッハパンチ: 威力40。先制わざ(優先度+1)。
はやてがえし: 威力65。先制わざ(優先度+3)。相手が先制攻撃わざを使おうとしているときのみ成功し、相手をひるませる(行動できない)。
きあいパンチ: 威力150。わざを出すまでに攻撃を受けると失敗する。
素早さが同じ場合におけるわざ同士の相性は以下の通りです:
マッハパンチ>きあいパンチ(きあいパンチは失敗)
きあいパンチ>はやてがえし(はやてがえしは失敗)
はやてがえし>マッハパンチ(マッハパンチは失敗)
マッハパンチ=マッハパンチ(両方成功する)
きあいパンチ=きあいパンチ(ランダムに選ばれた一人だけ成功)
はやてがえし=はやてがえし(ランダムに選ばれた一人だけ成功)
以上から三つのわざが三すくみの関係になっていることがわかるかと思います。ただしじゃんけんと違う点が三点あります:
わざによってダメージが異なる
わざによってあいこの判定が異なる
結果に確率的なブレがある(乱数・急所・あいこ判定)
この三点によってじゃんけんより複雑性の高く面白みのあるゲームとなっています。
レギュレーション
(元祖)エビワラーじゃんけんではレギュレーションがかっちりと定められています。肝となるのは全プレイヤーが同一ステータスのエビワラーを利用するという点です(詳細はここを参照)。ステータスが既知なので確定数が正確に計算できまして、具体的には以下の通りになります:
マッハパンチ: 乱数三発(64.4%、つまり35.6%で四発必要になる)
はやてがえし: 確定三発
きあいパンチ: 確定一発
はやてがえし一発 + マッハパンチ二発で確定
上記に見るように「きあいパンチ」を一度でも打てれば勝ちなのですが、それを防ぐために「マッハパンチ」を打ったり、それをさらに読んで「はやてがえし」を打ったりするなど読み合いが大事になってきます。
前置き: 通常のじゃんけんに最強手はある?
エビワラーじゃんけんにおける最強戦略を考える前にまず通常のじゃんけんについて考えましょう。興味がない方は飛ばしていただいて大丈夫です。
直感的にはじゃんけんに最強手はない気がしますよね。グーチョキパーのどれを出しても勝率は同じな気がします。それではどんな場合でも必ずグーを出すという戦略でいいのでしょうか?実はこの問いの答えはYesでありNoなのです。
仮に相手がグーチョキパーを1/3ずつの確率で繰り出してくる場合、もちろんグーを出せば1/3の確率で勝利することができます。
しかしながらもし相手にこちらの戦略(=必ずグーを出す)がリークしていたとしたらどうでしょうか。相手は必ずパーを出すことで必ずこちらに100%勝利することができてしまうのです。
戦略のリークは非現実的すぎるようにも思えますが、例えば100回連続じゃんけんをするようなケースを考えたら途中で相手はこちらの戦略(=必ずグーを出す)を見抜けそうですよね。このように戦略のリークは発生しうるのです。
では「必ずグーを出す」戦略ではなく「グーチョキパーの中からランダムに直前で選んで出す」という戦略を採用したらどうでしょうか。これなら相手に戦略がリークしようが勝率はちゃんと1/3になりますよね。
このように「選択肢の中から確率的に一つ選んで実行する」戦略をゲーム理論では混合戦略と言い、相手に戦略がリークしている場合に最も高い勝率を達成できる混合戦略を混合戦略のナッシュ均衡と呼びます。
じゃんけんにおける混合戦略のナッシュ均衡
それではじゃんけんにおける混合戦略のナッシュ均衡の求め方を考えてみましょう。
今回は自分も相手も混合戦略を取ってくると想定して考えます。ここでは自分がグー、チョキ、パーを出す確率をそれぞれ$${x_1,x_2,x_3}$$, 相手の確率を$${y_1,y_2,y_3}$$としましょう。また勝ちで1ポイント、引きわけで0.5ポイント、負けで0ポイントを得るとしましょう。この場合自分の獲得ポイントの期待値は次の式で表せます:
$${\textbf{x}^T A \textbf{y},}$$
where

なおこの設定だと上の式$${\textbf{x}^T A \textbf{y}}$$は勝率になっていることに注意です。
今回は自分の混合戦略がリークしていたとしても最高の期待値が出せるような混合戦略を求めてみましょう。自分の混合戦略がリークしていた場合、相手は対抗して最も勝てる混合戦略を選ぶと仮定します。具体的には次を最小化させるyを選択するとします:
$${\min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y},}$$
$${where \quad\textrm{S}=\{\textbf{x}|0\le\textbf{x}_i\le1, \sum \textbf{x}_i=1\},}$$
今回はこのyに対して最高の勝率が出せるxを求めたいので、具体的には次の式を最大化するようなxを求めます:
$${\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y},}$$
$${where \quad\textrm{S}=\{\textbf{x}|0\le\textbf{x}_i\le1, \sum \textbf{x}_i=1\}}$$
結果としてシンプルなmin-max問題に落ち着きました。これを解くことで$${x_1,x_2,x_3=1/3}$$という解が得られ、グーチョキパーを平等にランダムに選ぶ混合戦略が最適であるという結論が得られます。この解がいわゆる混合戦略のナッシュ均衡です。
(サラッと解を書きましたが上のmin-max問題を解くためには線形計画法などを用いる必要があります。pythonユーザであればnashpyを使うと簡単です。)
以上で通常のじゃんけんの話は終わりです。以降ではここまでのアプローチを利用して肝心のエビワラーじゃんけんの最強戦略を考察していきます。
単純化エビワラーじゃんけん: マッパ確二Ver.
実際のエビワラーじゃんけんは説明する上で複雑すぎるので、まずは少し単純化した問題を考えましょう。ここでは次の設定を考えます。
エビワラーのHPが2
「マッハパンチ」「はやてがえし」のダメージは必ず1(急所・乱数なし)、つまり確定二発
「きあいパンチ」のダメージは確定一発
この設定で勝ち負けポイント行列$${A}$$を考えましょう。今回は勝率を最大化したいので、行列の各要素に勝率を埋めていくことにしましょう。今回は自分と相手のHPがそれぞれPとQの状態で自分と相手がそれぞれAとBをわざとして選択した場合の勝率を$${p_{\text{自HP=P,敵HP=Q}}(\text{自技=A, 敵技=B})}$$で表記することにします。この設定における勝ち負けポイント行列、つまり勝率行列Aは次のようになります:

なお上記では"マ"=「マッハパンチ」、"は"=「はやてがえし」、"き"=「きあいパンチ」と表記しました。
次に各種の$${p_{\text{自HP=2,敵HP=2}}(\text{自技=A, 敵技=B})}$$について考えてみましょう。次の五つは異論ないでしょう。
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=マ, 敵技=マ})}$$: 両者ともわざ選択が同じなので勝率は両者とも同じ。故に0.5
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=は, 敵技=は})}$$: 同上の理由で0.5
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=き, 敵技=き})}$$: 同上の理由で0.5
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=き, 敵技=は})}$$: 自分が「きあいパンチ」を決めて勝利なので1
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=は, 敵技=き})}$$: 相手が「きあいパンチ」を決めて敗北なので0
では他の四つはどうでしょうか。例えば$${p_{\text{自HP=2,敵HP=2}}(\text{自技=は, 敵技=マ})}$$、つまり自分が「はやてがえし」を決めた場合の勝率はどうでしょうか。この場合自分のHPが2、相手のHPが1になって有利になるので勝率は0.5より大きくなりそうですが、具体的な値は自明ではありません。
そこで次に自分のHP=2、相手のHP=1の場合の勝率を調べてみましょう。
自分のHPが2、相手のHPが1の場合
自分のHPが2、相手のHPが1の場合における勝率行列Aの各要素を考えていきましょう:

まず次の六つは自分もしくは相手が確定で勝利する場合です。こちらは直感的にわかりやすいでしょう:
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=マ, 敵技=マ})}$$: 両者とも「マッハパンチ」を決めるが、相手のみHP=0になるので勝利。故に1
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=き, 敵技=き})}$$: どちらか一方がランダムで「きあいパンチ」を決めて勝利するので0.5
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=は, 敵技=マ})}$$: 自分が「はやてがえし」を決めて勝利するので1
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=マ, 敵技=き})}$$: 自分が「マッハパンチ」を決めて勝利するので1
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=き, 敵技=は})}$$: 自分が「きあいパンチ」を決めて勝利なので1
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=は, 敵技=き})}$$: 相手が「きあいパンチ」を決めて敗北なので0
次に、相手のみ「きあいパンチ」もしくは「マッハパンチ」を決めた場合はどうでしょうか。この場合自分のHP=1になり、両者が同じHPになります。故に勝率は0.5になりそうです:
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=マ, 敵技=は})}$$: 相手が「はやてがえし」を決めて両者のHPが同じになるので0.5
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=き, 敵技=マ})}$$: 相手が「マッハパンチ」を決めて両者のHPが同じになるので0.5
最後に両者とも「はやてがえし」を打った場合はどうでしょうか。この場合どちらか一方だけが「はやてがえし」を決めることになりますが、自分が決めれば勝ち、相手が決めれば両者のHPが1になって勝率0.5になるので、実際の勝率は$${0.5 * 1 + 0.5 * 0.5=0.75}$$になります:
$${p_{\text{自HP=2,敵HP=1}}(\text{自技=は, 敵技=は})}$$: 0.75
これらを代入すると勝率行列Aは次のようになります:
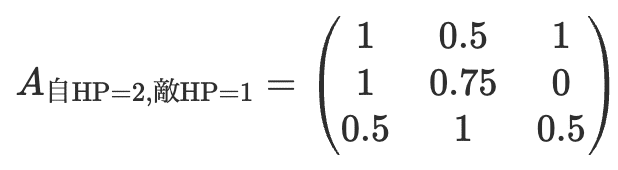
この行列を元に$${\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y}}$$を解くと自分と相手の混合戦略のナッシュ均衡はそれぞれ
$${(x_1,x_2,x_3)=(0.333, 0.444, 0.222), (y_1,y_2,y_3)=(0.333, 0.222, 0.444)}$$
と求めることができます。
これらxとyを代入して、このナッシュ均衡に従った場合の自分の勝率は$${p_{\text{Nash: 自HP=2,敵HP=1}}()=\textbf{x}^T A \textbf{y}=0.778}$$となるわけです。
自分と相手のHPが2の場合
上記から自分のHPが2、相手のHPが1となった場合におけるナッシュ均衡に従った場合の勝率は$${p_{\text{Nash: 自HP=2,敵HP=1}}()=0.778}$$となることがわかりました。なお自分のHPが1、相手のHPが2の場合はこの真逆であり、1からこの数字を引けばいいので$${p_{\text{Nash: 自HP=1,敵HP=2}}()=1-p_{\text{自HP=2,敵HP=1}}()=1-0.778=0.222}$$になりますね。
これらを踏まえ、両者のHPが2の場合について再び考えてみましょう。次のことが言えるようになります:
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=マ, 敵技=き})}$$: 自分が「マッハパンチ」を決めて相手のHP=1の状態に遷移する。よって勝率は$${p_{\text{Nash: 自HP=2,敵HP=1}}()=0.778}$$
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=は, 敵技=マ})}$$: 自分が「はやてがえし」を決めて相手のHP=1の状態に遷移する。よって勝率は$${p_{\text{Nash: 自HP=2,敵HP=1}}()=0.778}$$
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=き, 敵技=マ})}$$: 相手が「マッハパンチ」を決めて自分のHP=1の状態に遷移する。よって勝率は$${p_{\text{Nash: 自HP=1,敵HP=2}}()=0.222}$$
$${p_{\text{自HP=2,敵HP=2}}(\text{自技=マ, 敵技=は})}$$: 相手が「はやてがえし」を決めて相手のHP=1の状態に遷移する。よって勝率は$${p_{\text{Nash: 自HP=1,敵HP=2}}()=0.222}$$
この四つと当初の五つの値を合わせると両者のHP=2の場合の勝率行列$${A_{\text{自HP=2,敵HP=2}}}$$の全ての要素の値がわかりますね。具体的には次のようになります:

この行列を元に$${\max_{\textbf{x}\in \textrm{S}} \min_{\textbf{y}\in \textrm{S}} \textbf{x}^T A \textbf{y}}$$を解くと自分と相手の混合戦略のナッシュ均衡はそれぞれ
$${(x_1,x_2,x_3), (y_1,y_2,y_3)=(0.474, 0.263, 0.263)}$$
となります。両者とも混合戦略が同じ、かつ「マッハパンチ」の選択確率が高いのは直感的ですね。また「はやてがえし」と「きあいパンチ」の選択確率が同じなのも面白いですね。
自分のHPがN、相手のHPがMの場合
次により一般的な場合、具体的には自分のHPがN、相手のHPがM(NとMは自然数)の場合について考えてみましょう。
この場合「マッハパンチ」「はやてがえし」は(ダメージが1という仮定から)確定N発/M発になります。なお「きあいパンチ」に関しては説明の都合上確定一発とします。
この場合の勝率行列$${A_{\text{自HP=N,敵HP=M}}}$$を考えていきましょう:

次の三つは自明です:
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=き, 敵技=は})}$$: 自分が「きあいパンチ」を決めて勝利なので1
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=は, 敵技=き})}$$: 相手が「きあいパンチ」を決めて敗北なので0
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=き, 敵技=き})}$$: どちらか一方がランダムに「きあいパンチ」を決めて勝利するので0.5
ではこの二つ以外の場合、例えば自分だけが「マッハパンチ」を決めた場合はどうでしょうか。この場合相手のHPがM-1の状態に遷移するので、混合戦略のナッシュ均衡に従うのであれば勝率は$${p_{\text{自HP=N,敵HP=M}}(\text{自技=マ, 敵技=き})=p_{\text{Nash: 自HP=N,敵HP=M-1}}()}$$となります。同様に:
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=マ, 敵技=マ})=p_{\text{Nash: 自HP=N-1,敵HP=M-1}}()}$$
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=は, 敵技=は})=0.5 * p_{\text{Nash: 自HP=N,敵HP=M-1}}() + 0.5 * p_{\text{Nash: 自HP=N-1,敵HP=M}}()}$$
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=マ, 敵技=き})=p_{\text{Nash: 自HP=N,敵HP=M-1}}()}$$
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=は, 敵技=マ})=p_{\text{Nash: 自HP=N,敵HP=M-1}}()}$$
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=マ, 敵技=は})=p_{\text{Nash: 自HP=N-1,敵HP=M}}()}$$
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=き, 敵技=マ})=p_{\text{Nash: 自HP=N-1,敵HP=M}}()}$$
となります。以上で見るように勝率行列$${A_{\text{自HP=N,敵HP=M}}}$$の各要素は、NとM(のどちらかもしくは双方)が一つ小さい場合における勝率を元に計算することができるのです。これを踏まえると、自分が気になる(N, M)の組合せから始めて再帰的に各場合の勝率行列Aおよびナッシュ均衡と勝率を求めていけば、最終的には(N, M)におけるナッシュ均衡と勝率を求めることができる、というわけです。
# 実装面
再帰を使えば勝率およびナッシュ均衡を計算することができますが、実装的には「メモ化再帰」もしくは「動的計画法」を使うと楽です。気になる方は調べてみてください。この問題に関しては「メモ化再帰」を使うとより高速な計算ができます。
本題: エビワラーじゃんけん
上記では単純化したエビワラーじゃんけんについて考えてきました。ここでは本題の元祖エビワラーじゃんけんについて考察していきます。
元祖エビワラーじゃんけんにおいても概ね上記のやり方に従うのですが、大きな違いとして「マッハパンチ」「はやてがえし」のダメージが急所・乱数により確率的に変動するという点があります(具体的なダメージ分布については最後の「おまけ1」の章をご参照ください)。
実際に勝利行列Aの計算をする際にはこの変動を加味する必要があります。例として自分だけが「はやてがえし」を決めた場合を考えましょう。まず「はやてがえし」のダメージがxで固定だとすると、$${p_{\text{自HP=N,敵HP=M}}(\text{自技=は, 敵技=マ})=p_{\text{Nash: 自HP=N,敵HP=M-x}}()}$$となります。ただし実際にはこのダメージは確率的にブレるので、勝率の期待値を計算して用いる必要が生じます:
$${p_{\text{自HP=N,敵HP=M}}(\text{自技=は, 敵技=マ})=\sum_x p_{\text{はやてがえし}}(x) * p_{\text{Nash: 自HP=N,敵HP=M-x}}()}$$
ここで「はやてがえし」のダメージがxになる確率を$${p_{\text{はやてがえし}}(x)}$$と表記しました。このように勝率行列の各要素の計算において勝率の期待値を用いれば実際のエビワラーじゃんけんにおける正しい勝率とナッシュ均衡の計算をすることができるようになります。
混合戦略のナッシュ均衡の数値解
実際にありえるHPの組合わせそれぞれについて勝率と混合戦略のナッシュ均衡を計算しました。結果は長いのでこちらのスプレッドシートに載せておきます。
以下でいくつか見ていきましょう:
1ターン目における混合戦略のナッシュ均衡
両者:
マッハパンチ: 60.6%
はやてがえし: 17.7%
きあいパンチ: 21.7%
1ターン目は「マッハパンチ」を六割ほどの確率で選択するのが望ましいことがわかります。面白いですね。
1ターン目で自分が「はやてがえし」を決めた場合における2ターン目の混合戦略のナッシュ均衡
非急所で55ダメージだとする。この場合自分のHPは125、相手のHPは80となる。
(なお相手の残りHPは大きい画面に定規を当てることで計測できるとする)
自分:
マッハパンチ: 60.9%
はやてがえし: 5.1%
きあいパンチ: 34.1%
相手:
マッハパンチ: 54.9%
はやてがえし: 32.5%
きあいパンチ: 12.6%
自分の勝率は67.4%
「はやてがえし」を決めた後の方が1ターン目より「きあいパンチ」の選択確率が大きくなっていることが面白いですね。
1ターン目で両者とも「マッハパンチ」を決めた場合における2ターン目の混合戦略のナッシュ均衡
両者とも非急所で40ダメージだとする。この場合自分と相手のHPは85となる。
両者:
マッハパンチ: 53.9%
はやてがえし: 18.9%
きあいパンチ: 27.2%
こちらも1ターン目より「きあいパンチ」の選択確率が大きくなっていることが面白いですね。
考察
以上に示したとおり各状態における混合戦略のナッシュ均衡を求めることができました。これらの混合戦略のナッシュ均衡に従えばどんな相手が来ても勝率を50%以上にすることができます。
ではこの戦略に従って対人戦を行うのがベストか?というとそう断言するのは難しいのかなと思います。
実際の各人の選択肢には"クセ"があり、今回紹介した選択確率分布とは異なる分布に従ってわざ選択を行うと考えるのが自然です。いわゆる「ふいうち」択も初心者と上級者でクセが違いますよね?実際の対戦では相手のわざ選択確率分布を推定し、かつその選択確率分布に対して特に強いわざ選択確率分布を考え、それに従ってわざ選択をすることが勝率をさらに高める上で大事になるのかなと思います。
こうなると多腕バンディット的な問題についての最適な戦略について考えることになり、その手の問題に対して最適な戦略を証明付きで提示できる人は現生人類に果たしているのか謎です。
雑感
厳密な数値解が求まると楽しいですね。マッハパンチつよし。
○○1on1系(シビルドン1on1とか)の設定でも同じアプローチで混合戦略を計算できたりしそうです。まあ大抵のポケモンは組合せ爆発で死ぬかもしれませんが…
エビワラーじゃんけんにはダブルバトル版・マルチバトル版もあるようです。こっちも頑張ればナッシュ均衡を計算できそう。
ここまで長い記事に目を通していただき大変ありがとうございました!
(おまけ1)ダメージ分布
今回の解析で使用したダメージ分布は以下の通りです。リストの中からランダムにダメージが選ばれると考えてください:
マッハパンチ(非急所、確率は23/24): [39, 39, 39, 40, 40, 40, 42, 42, 42, 43, 43, 43, 45, 45, 45, 46]
マッハパンチ(急所、確率は1/24): [58, 58, 60, 60, 60, 61, 61, 63, 63, 64, 64, 66, 66, 67, 67, 69]
はやてがえし(非急所、確率は23/24): [51, 52, 52, 54, 54, 54, 55, 55, 57, 57, 57, 58, 58, 60, 60, 61]
はやてがえし(急所、確率は1/24): [76, 78, 79, 79, 81, 81, 82, 84, 84, 85, 85, 87, 88, 88, 90, 91]
(きあいパンチは急所関係なく確定一発なので載せません)
ダメージ計算はこちらのページを参考にさせていただきました。ダメージに飛び値があるのが気になるかもしれませんが、最小・最大ダメージはポケソルのダメ計ツールと同じ結果なので正しいと思います。多分。
(おまけ2)参考文献
休歌さんの元ネタ記事です。
とも湯さんの解説動画です。
今日ポケチャンネルさんの動画です。いろはさんが「初手はマッハパンチでお茶を濁せる」(意訳)と述べられていますが、今回の解析結果とも一致しているかと思います。
昔書いた記事です。こちらもよければぜひ。そのうちnoteに移します。
この記事が気に入ったらサポートをしてみませんか?
