
[閲覧注意] アポロニオス『円錐曲線論』第Ⅰ巻命題11,20
本稿はアルキメデス『放物線の求積』における放物線の性質の補足説明のために用意したものです.これだけ読んでも,(多分)一部の方しか楽しめません.古代と現代の曲線の生成についての認識の違いを感じることができると思います.
序.
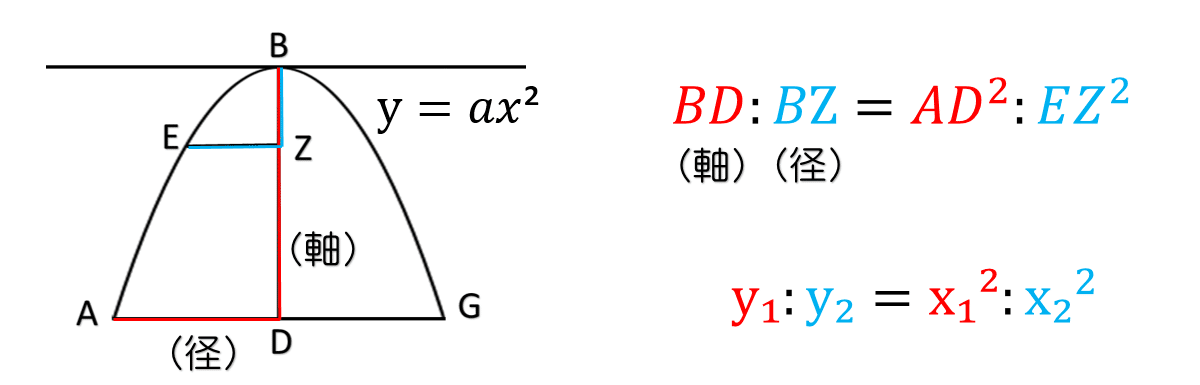
アルキメデスは,放物線の軸と径の長さの比例関係は,失われた『円錐曲線原論』で証明されているといいます.現代的な視点では(原点を頂点とする)放物線はy=ax²(もしくは y²=px)で定義されますので,軸(y)と径(x)の比例関係が証明を必要とするというのは違和感があることでしょう.しかし,古代ギリシャ人には曲線を方程式で表わすという概念はありませんでした.
放物線は円錐の切り口によって生成されます.
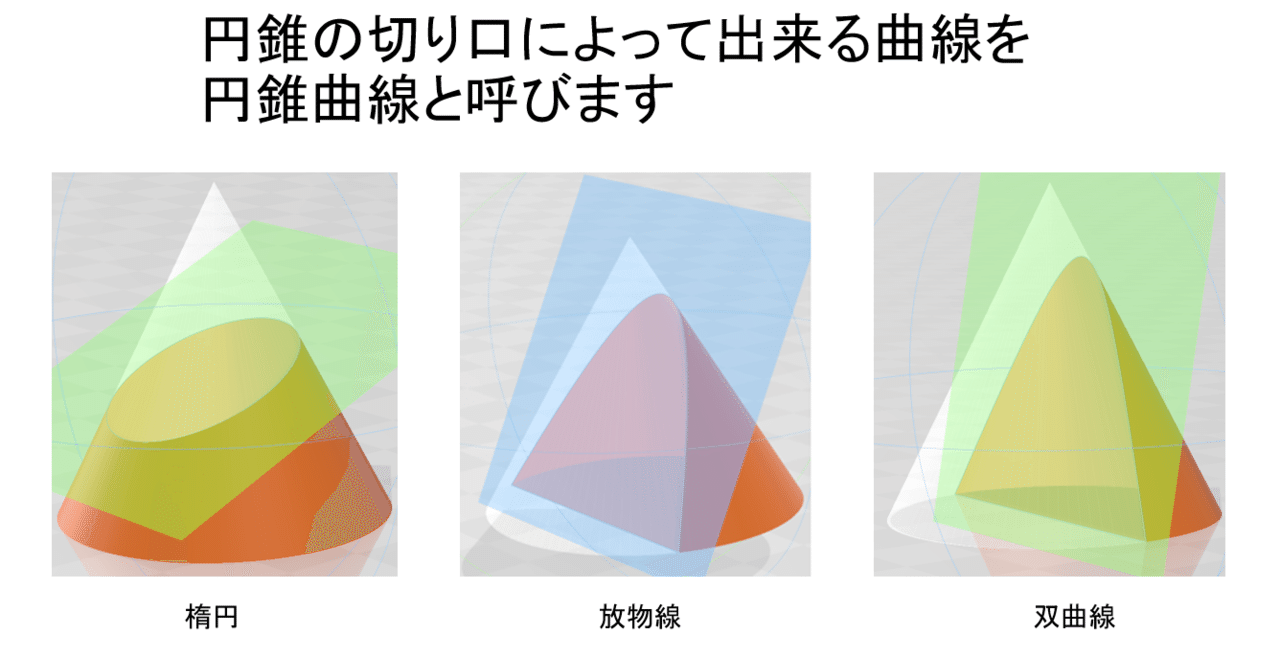
本稿では,放物線の軸と径の比例関係についての証明を行う,アポロニオス(前200年頃活動)の『円錐曲線論』第Ⅰ巻命題11と20の証明をご紹介します.
1.円錐の断面としての放物線
まず命題11では次の関係を証明します.これは曲線を方程式で表わす立場では, y²=px のことだと分かります.
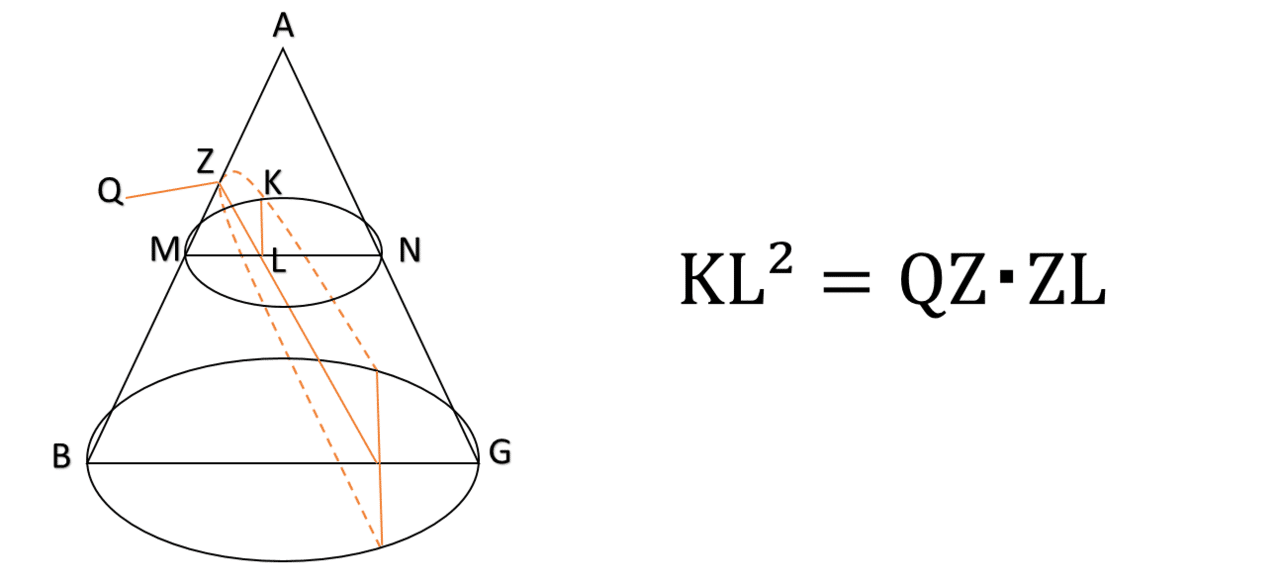
放物線の「開き」を表わすパラメータ p と同じ働きをする放物線の軸(ZL)に垂直な線分ZQを導入するわけですね.pが大きければ放物線の開き具合も大きくなります.
KL²=QZ・ZL は現代の視点では曲線の「定義」なのですが,古代ギリシャではこれを「証明の対象」とします.証明の出発点は次の関係です.
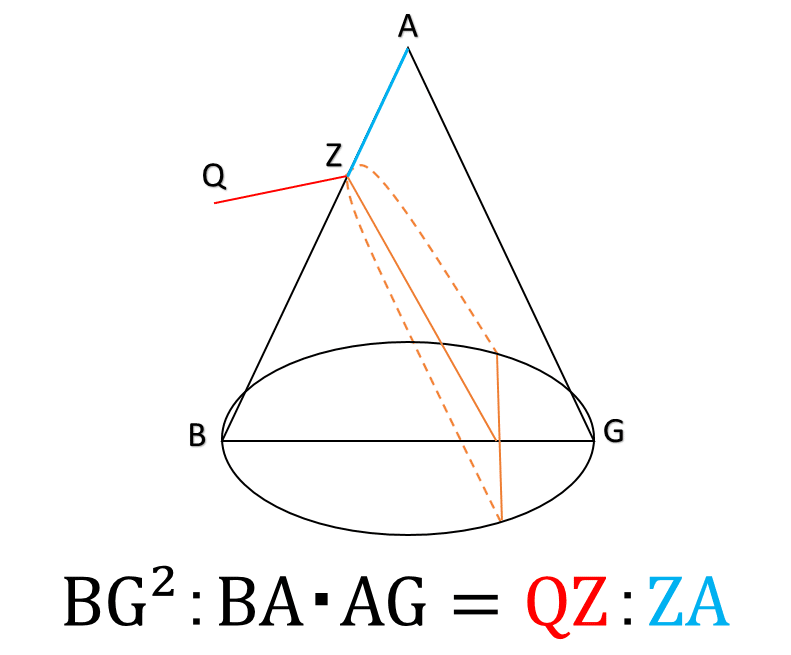
一体この比例関係は何を表現したいのでしょうか? まず左辺が一定の場合を考えましょう. ZAが長くなればなるほど,QZも長くなりますよね.そしてZAが長い方が,放物線の開きも大きくなります.
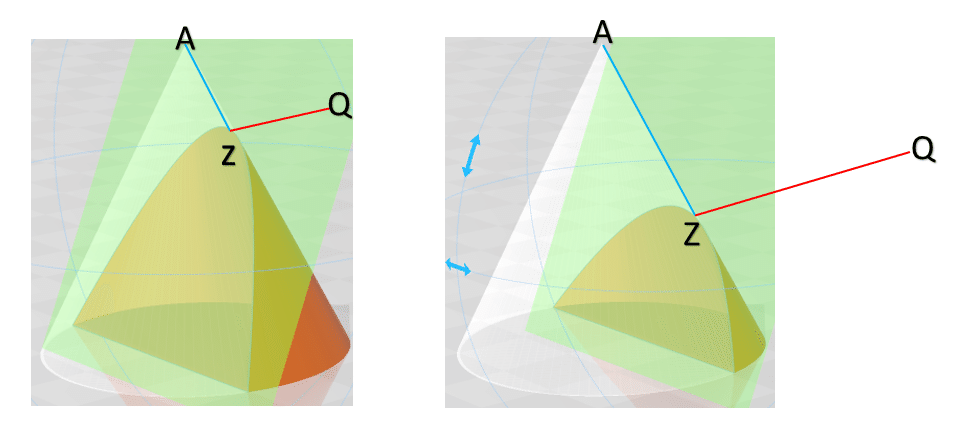
一方,右辺が一定の場合, 左辺の変化は円錐の形状を表現します.
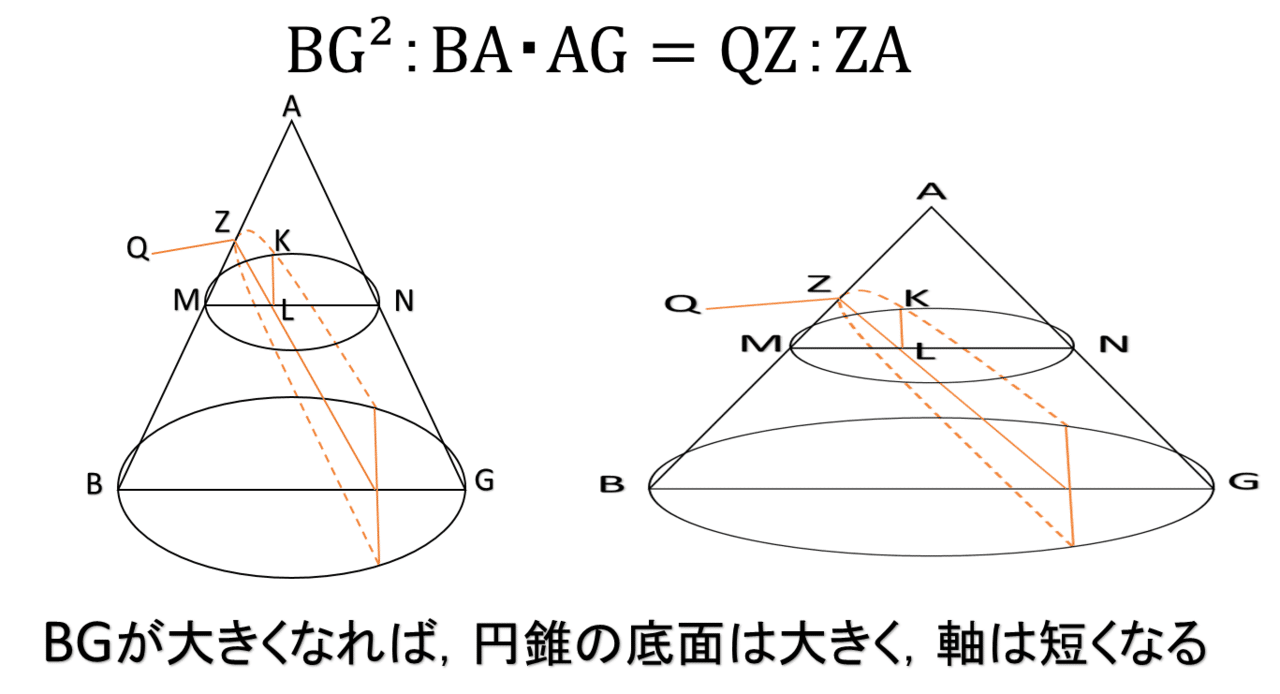
放物線の開き具合を表現するパラメータである線分ZQを,BG²:BA・AG=QZ:ZA の関係によって定義するのはなかなか巧いやり方です.
2.命題11
準備ができました.それでは証明を始めましょう.
KL²=QZ・ZL を証明します
まずは円錐を真横から見てみます.繰り返しになりますが,BG²:BA・AG=QZ:ZA が議論の出発点です.
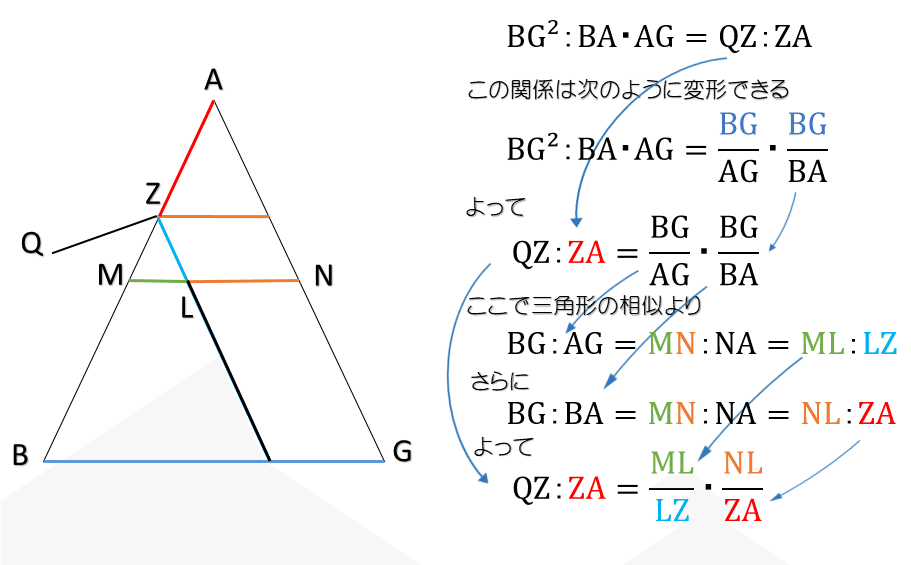
ここで円錐を透視図で立体的に見てみましょう.
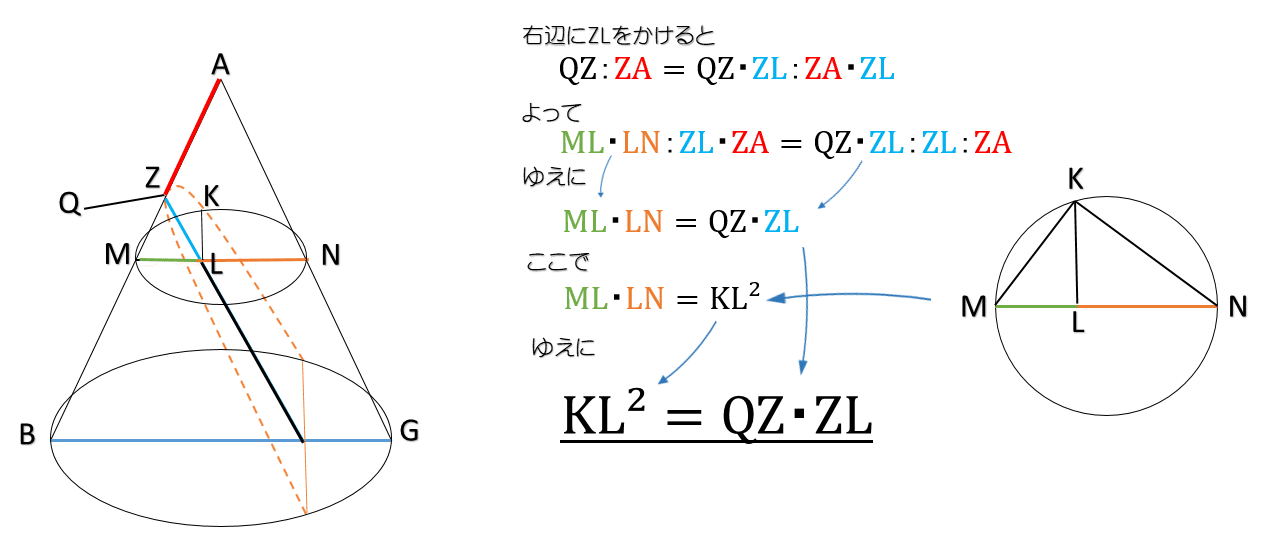
証明ができましたね.
3.命題20
それでは,いよいよ軸と径の比例関係を証明します.
DZ²:GE²=AZ:AE を証明することになります.
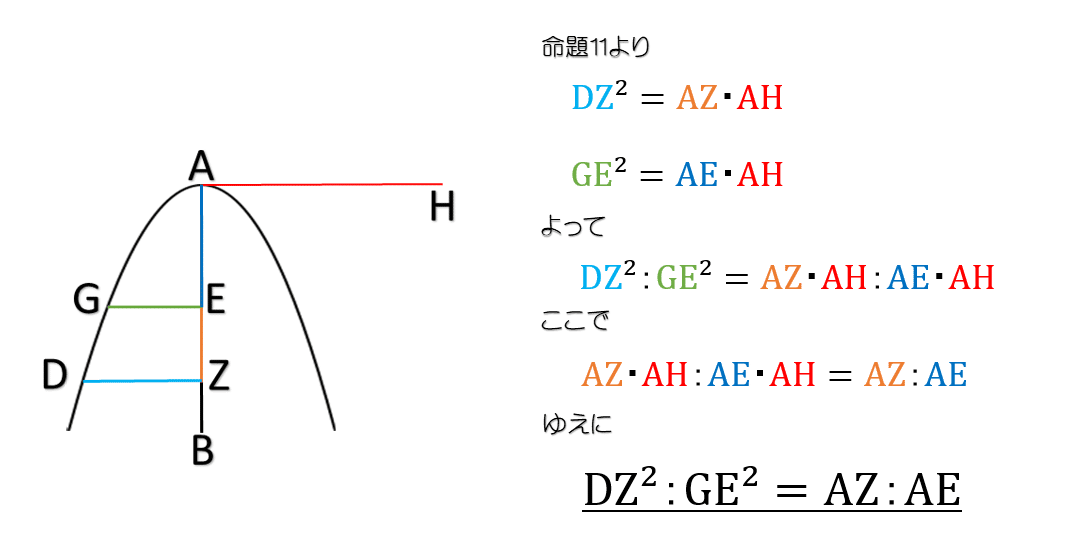
4. 最後に
ここまで KL²=QZ・ZL というように,二乗や積を用いて比例関係を表現してきましたが,この表現は古代の数学に誤解を招く恐れがあります.アポロニオスは KL²=QZ・ZL を次のような言い回しで表現します.
λέγω, ὅτι τὸ ἀπὸ τῆς ΚΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΘΖΛ. 私は言う,KL上〔の正方形〕はQZ,ZL〔を辺とする平行四辺形〕に等しい.
彼らは図形の大きさをそのまま比較をしているのであって,二乗や積の操作の可能になる「量」を取り扱ってはいないのです.現代の私たちに理解しやすくするために,本稿では図形の大きさを量として扱いました.ですが,代数(解析幾何)という便利で優れた道具が欠如していたから,現代の私たちから見て回りくどい表現をしていたと考えるべきではありません.図形から量を切り離して考えるということへの「関心が欠如」していたとすべきでしょう.
参考文献
・斎藤憲『ユークリッド原論の成立』東京大学出版会,1997年.
・L. V.Heiberg, Apollonii Pergaei quae Graece exstant cum commentariis antiquis, 1891, 93.
・R. Catesby Taliaferro /Michael N. Fried , Conics Books I-IV ,2013.
この記事が気に入ったらサポートをしてみませんか?
