
θが小さいとき sinθ=θ
高校の物理で振り子の周期の式が出てくる。
T=2π√ (l / g ) l:振り子の長さ、g:重力加速度
この式は振り子の長さが同じなら、その振れ幅の大きさによらず周期が一定であることを示している。ガリレオ・ガリレイが発見したと伝えられる振り子の等時性を式化したものである。
さて、この式を導くのに「振り子の振れ幅 θが小さいので sinθ=θ 」という近似が使われる。しかし、このことを知った高校生のわたしは非常に不快な気持ちになった。物理学というものは物体の運動の様子を厳密に表すと思っていたのが、いきなり θが小さいときは sinθ=θ (=tanθ もあり)といわれ、裏切られたような気持ちになった。いったい θ が小さいって、どのくらいの小ささなのか。どういう時に近似するのか。してもいいのか。わたしには式を導くためのご都合主義にしか思えなかった。
今回、古典力学を再学習する中で単振り子の運動に再会したので、振り子の周期について高校物理での導出と近似を行わない厳密解について調べてみた。
1.θが小さいって、どのくらい?
まず、sinθ = θ としてもよいθの範囲とはどのくらいかを調べた。

上に示す通り、sinθとθの差が1%以内になるのは θ<14° 、5%まで認めると 31° 、10%までなら43° である。
等しいという表現が相応しいのは差が1%までだろう。つまり「θが14° までの小ささであれば sinθ = θ」としてもよい。
(θ とは鉛直線からの角度なので −14°<θ<14°の振れ、つまり振れ幅が14*2=28°までならこの近似をしてもよいことになる)
ちなみに、tan の場合はもう少し小さくて10° である。
(おまけ)数Ⅲでこんなことをした。
ただし、ロピタルの定理を使うのではなく図形を書いた説明だった。

ちなみにマクローリン展開では
sinθ=θ - 1/6 θ^3 + 1/120 θ^5 ‥ である
2.高校物理での導出
高校の復習からはじめる。
実はどんなふうに式を作ったのか思い出せなかったので、書店の参考書の立ち読みとネットでの検索を行った。
それによると
まず質量mのおもりの接線方向の運動方程式 F=–mg sinθを立てる。
そのあと、θが小さいので接線方向とx軸方向を同じとして
運動方程式の sinθに x/l (=θ)を代入して F=–(mg/l)x を得る。
さて、これは単振動の運動方程式 F= –○ x と同じ形なので
ω^2=g/l 、ω=√(g/l) 、よって T=2π/ω=2π√(l/g)
また、 x=Asin(ωt+α) (単振動の定義より)

高校では運動方程式を微分方程式で記述して解くことができないので、こういう導き方をしている。( 物理の力学分野は高1か高2、微分方程式は理系選択の数Ⅲで学習する)
まず、単振動をx=sin(ωt+α) と定義する。
そして、この定義より加速度は a=Aω^2(円運動の射影)
よって、運動方程式は F=ma=–Aω^2 x
この形 F=–○x は単振動だよね。
だから、ω= ‥‥ 、よってT= ‥‥
と持っていく。
ちなみに 「θがどのくらいの小ささか」の具体的な説明がされているものはなかった。また、sinθ = θ をださないのが最近の書き方のようだ。
3.微分方程式による解
では、微分方程式を作って解いてみよう。
立式には接線方向の運動方程式から導出する方法と、力学的エネルギーを求めてエネルギー保存則(dE/dt=0)から導出する方法の2つがある。
得られる式は d2θ/dt2 = – g/l sinθ である。

3−1.近似解(sinθ=θ)
d2θ/dt2 = – g/l sinθ を
まず、θが小さいので sinθ=θ (具体的には θ<14°)
g/l=ω^2 とおいて与式に代入する
d2θ/dt2 = – ω^2 θ
これを解くと、 θ=Asin(ωt+α)
g/l=ω^2 、ω=√(g/l) 、よって T=2π/ω=2π√(l/g)
同次形の2階微分方程式の解法はいくつかある。
1が分かりやすいと思うが、2と3もマニアックで魅力的だ。


3−2.厳密解(sinθ≠θ)
今度は sinθ をθに近似せずに d2θ/dt2 = – l/g sinθ のまま解く。
手順は以下の通り。
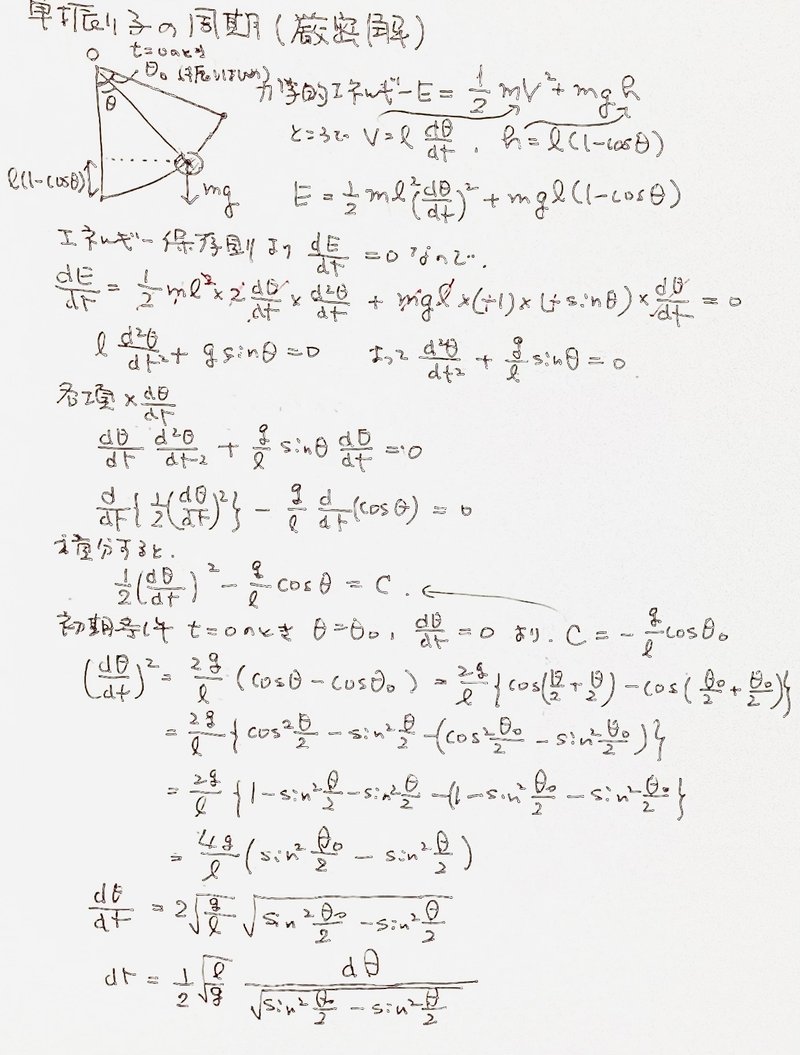
周期T は

となる。
積分の部分はルジャンドルの標準形における第一種楕円積分の積分範囲を0からπ/2までとしたもので第一種完全楕円積分と呼ばれる。これは高校で扱える数学ではない。しかしTがθoの関数であることはわかる。
よって、振り子の周期Tは振り子の長さだけではなく振れ幅θoにも関係する。
というわけで、厳密には振り子の等時性は成り立たない。
4.厳密解と近似解のずれ
では、近似解と厳密解はどのくらいずれているのか。
振り子の等時性はどの程度成り立ち、また成り立たないのか。計算してみよう。
g=9.8 m/sec2、l=0.5mとする。
近似解は、Ta=2π√ (l / g ) に代入すればよい。
厳密解は、積分内をマクローリン展開したのち積分する。

4−1.振り子の運動の様子(厳密解)
上の式からわかるように周期Tは触れ角θoが大きいほど大きくなる。
θoに具体的な値をいくつか入れて周期Tを求め、振り子の運動の様子をグラフ化した。確かにずれている。

4−2.振れ角θo vs ずれ率
近似解Taと厳密解Tのずれ率を求めると
その差が1%以内になるのは、θo<23°、5%以内ならθo< 51° である。

「sinθ = θ」の近似に比べて、周期の振れ幅の許容範囲のほうが1.5倍以上大きい。
この結果は、振り子の動きがよくわかるように振れ幅を大きくしても、それほど大きな誤差は生まないと言ってもよいのかもしれない。そういう意味では「等時性は成り立つ」。
4−3.触れ角θo vs 周期T
今度は、ずれ率ではなく、ずれの値(T–Ta)で考える。

振れ角θo=20°の時の厳密解と近似解のずれは0.01秒であり、60°の時は0.1秒である。その差は約0.1秒(正確には 0.09秒)であり、わずかのように見えるが、例えば10往復では1秒のずれである。2つの同じ長さの振り子を振れ角20°と60°で同時に振った時、10往復(約14秒)後には1秒のずれとなる。明らかに「等時性が成り立たない」ことに気づくだろう。
というわけで、等時性は成り立つような、成り立たないような悩ましいことになる。
5.まとめ
わたしの個人的な sinθ=θ への反感(θ<14° で誤差1%以内)から始まった議論であったが、実は周期Tはもっと大きなθ(θ<23° で誤差1%以内)も認めてしまうことがわかった。振り子の等時性は厳密には成り立たないが、近似解とのずれはわずかである。小中学生の実験、いや高校生の実験であっても、そのずれは実験上の測定値の誤差に隠れる可能性が高い。(わたし自身も思い当たる。大雑把な実験をしていた)実は sinθ = θ は大した問題ではなかった。やはりこの近似は高校生(あるいは力学はさらっと流すだけの大学生)が解くための都合である。まさに冒頭に書いた通りだった。
ガリレイは寺院の天井にぶら下がるランプの揺れの周期を自身の脈拍で測り、等時性を発見したと伝えられている。T=8√(l/g) の式も理論的に導いていたらしい。( T=2π√(l/g) とそれほど大きくずれていない)振り子時計も考案していたらしい。のちに厳密解が求められ、今度は本当に等時性が成り立つサイクロイド型振り子がホイヘンスによって考案されることによって、この問題は解決した。
この記事が気に入ったらサポートをしてみませんか?
