２次曲線､主軸変換

連成振動を原島鮮「力学Ⅱ」に従って進めていたら、主軸変換という言葉が出てきた。なんのこっちゃウーロン茶である。主軸変換でググると行列の対角化がまた出てきた。さらに２次曲線。。　もう下流に戻れないのではと不安になりながら遡っていった。

１ ２次曲線の確認

円､楕円､双曲線､放物線のことを２次曲線といい、
　$${ax^2+bxy+cy^2+dx+ey+f=0}$$(1)の形で表現され、
　$${b^2-4ac<0}$$のとき 楕円
　$${b^2-4ac>0}$$のとき 双曲線
　$${b^2-4ac=0}$$のとき 放物線　である。
1-1 放物線
　定点（焦点$${\text{F}(p,0)}$$）と定直線（準線$${x=-p}$$）からの距離が等しい
　点$${\text{P}(x,  y)}$$の軌跡である。（$${p\neq0}$$）

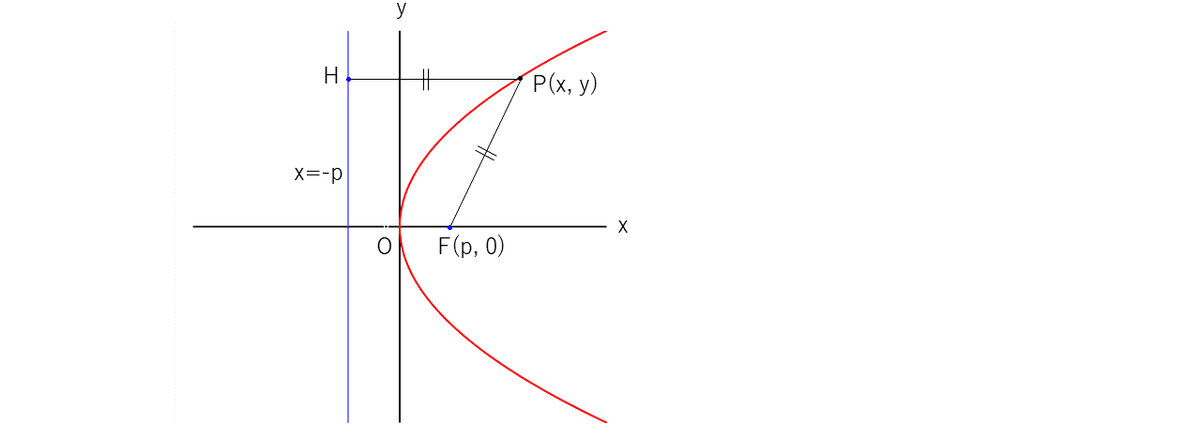
　$${\overline{\text{PF}}=\overline{\text{PH}}}$$より　$${\sqrt{(x-p)^2+y^2}=|x-(-p)|}$$
　２乗して　$${(x-p)^2+y^2=(x+p)^2}$$
　$${x^2-2px+p^2+y^2=x^2+2px+p^2}$$
　よって　$${y^2=4px}$$ (2)（放物線の標準形）
　または$${x}$$､$${y}$$を入れ替えて　$${x^2=4py}$$ (3)（放物線の標準形２）
　(2)は(1)において$${a=b=0}$$､(3)は$${b=c=0}$$なので
　$${b^2-4ac=0}$$である。
1-2 楕円
　２定点（焦点$${\text{F}(c,0),  \text{F'}(-c,0)}$$）からの距離の和（$${2a}$$とする）が等しい
　点$${\text{P}(x,  y)}$$の軌跡である。（$${c\neq0,  a>c>0}$$）

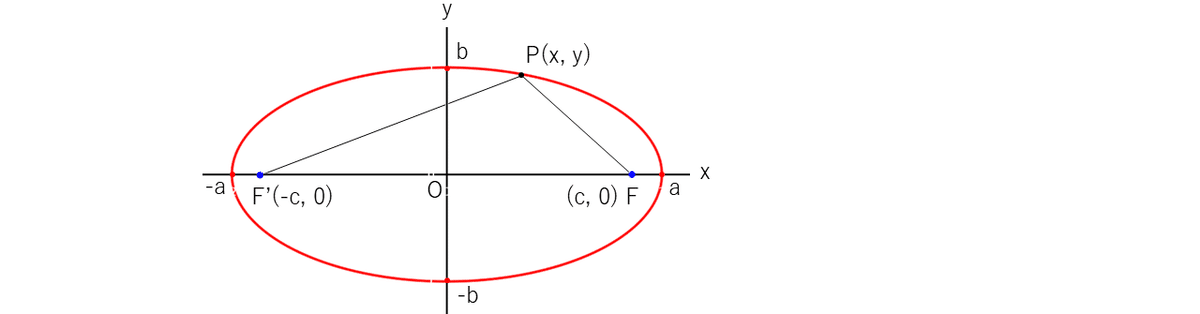
　$${\overline{\text{PF}}+\overline{\text{PF'}}=2a}$$より　$${\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a}$$
　$${\sqrt{(x-c)^2+y^2}=2a-\sqrt{(x+c)^2+y^2}}$$
　２乗して
　$${(x-c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2}$$
　$${x^2-2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2}$$
　$${-2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx}$$
　$${4a\sqrt{(x+c)^2+y^2}=4a^2+4cx}$$
　$${a\sqrt{(x+c)^2+y^2}=a^2+cx}$$
　２乗して
　$${a^2x^2+2a^2cx+a^2c^2+a^2y^2=a^4+2a^2cx+c^2x^2}$$
　$${a^2x^2+a^2c^2+a^2y^2=a^4+c^2x^2}$$　$${(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)}$$
　$${\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1}$$
　$${a^2-c^2=b^2}$$とおくと　$${\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1}$$(4)（楕円の標準形）
　(1)において $${a=\dfrac{1}{a'^2},  b=0,  c=\dfrac{1}{b'^2}}$$なので
　$${b^2-4ac=0-4×\dfrac{1}{a'^2}×\dfrac{1}{b'^2}<0}$$である。
1-3 双曲線
　２定点（焦点$${\text{F}(c,0),  \text{F'}(-c,0)}$$）からの距離の差（$${2a}$$とする）が等しい
　点$${\text{P}(x,  y)}$$の軌跡である。（$${c\neq0,  a>c>0}$$）

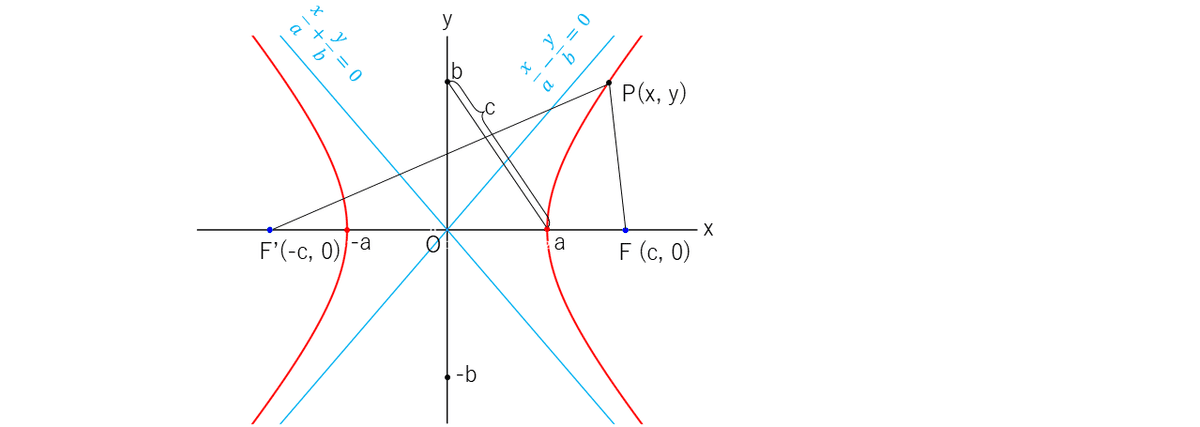
　$${\overline{\text{PF}}-\overline{\text{PF'}}=\pm2a}$$より　$${\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm2a}$$
　$${\sqrt{(x-c)^2+y^2}=\pm2a+\sqrt{(x+c)^2+y^2}}$$
　2乗して
　$${(x-c)^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2}$$
　$${x^2-2cx+c^2+y^2=4a^2\pm4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2}$$
　$${\mp4a\sqrt{(x+c)^2+y^2}=4a^2+4cx}$$　$${\mp a\sqrt{(x+c)^2+y^2}=a^2+cx}$$
　２乗して
　$${a^2x^2+2a^2cx^2+a^2c^2+a^2y^2=a^4+2a^2cx+c^2x^2}$$
　$${(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)}$$
　$${\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1}$$　　$${\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2}=1}$$
　$${c^2-a^2=b^2}$$とおくと　$${\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1}$$(5)（双曲線の標準形）
　漸近線は $${\dfrac{x}{a}\pm\dfrac{y}{b}=0}$$である。
　(1)において $${a=\dfrac{1}{a'^2},  b=0,  c=-\dfrac{1}{b'^2}}$$なので
　$${b^2-4ac=0-4×\dfrac{1}{a'^2}×\Big(-\dfrac{1}{b'^2}\Big)>0}$$である。 
他にも平行移動､離心率､媒介変数表示などいくつか要があるが、ここで必要な前提ではない。以上ザクっと復習した。

２ 主軸変換

２次曲線の一般形を以下のように変形する。（のちの変形の都合で$${b}$$は$${2b}$$とする。
　$${ax^2+2bxy+cy^2+dx+ey+f=0}$$(1)（２次曲線の一般形）
　$${ax^2+bxy+bxy+cy^2+dx+ey+f=0}$$
　$${(ax+by)x+(bx+cy)y+dx+ey+f=0}$$
　$${\begin{bmatrix}ax+by         bx+cy\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+f=0}$$
　$${\begin{bmatrix}x     y\end{bmatrix}\begin{bmatrix}a     b\\b      c\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+f=0}$$　(6)

ここで$${\bm{A}=\begin{bmatrix}a     b\\b      c\end{bmatrix}}$$とする。
　$${\bm{A}}$$に対する固有値:$${\lambda_1, \lambda_2}$$
　固有ベクトル:$${\bm{x_1},  \bm{x_2}}$$（直交している）
　規格化された固有ベクトル:$${\bm{u_1},  \bm{u_2}}$$（　　〃　　）
　対角化ベクトル:$${\bm{P}=\begin{bmatrix}\bm{u_1}      \bm{u_1}\end{bmatrix}}$$（規格化されている）
　$${\bm{P}}$$の逆ベクトル:$${\bm{P}^{-1}}$$
　$${\bm{P}}$$の転置ベクトル:$${{^t\bm{P}}}$$（$${{^t\bm{P}}=\bm{P}^{-1}}$$である）
とする。
以上より
　$${\begin{bmatrix}x\\y\end{bmatrix}=\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}}$$(7)、また$${\begin{bmatrix}x'\\y'\end{bmatrix}={^t\bm{P}}\begin{bmatrix}x\\y\end{bmatrix}}$$(8)、$${^t\bm{P}\bm{A}\bm{P}=\begin{bmatrix}\lambda_1     0\\0      \lambda_2\end{bmatrix}}$$(9)

では、変形をはじめる
　$${\begin{bmatrix}x     y\end{bmatrix}\begin{bmatrix}a     b\\b      c\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+f=0}$$　(6)
　$${\begin{matrix}\\ \end{matrix}^t\begin{bmatrix}x\\ y\end{bmatrix}\bm{A}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+f=0}$$
(7)を代入
　$${\begin{matrix}\\ \end{matrix}^t\bigg\{\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}\bigg\}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+f=0}$$
　$${\begin{matrix}\\ \end{matrix}^t\begin{bmatrix}x'\\y'\end{bmatrix}{^t\bm{P}}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+f=0}$$
(9)を代入
　$${\begin{bmatrix}x'   y'\end{bmatrix}\begin{bmatrix}\lambda_1     0\\0      \lambda_2\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+f=0}$$
　$${\begin{bmatrix}\lambda_1x'   \lambda_2y'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+\begin{bmatrix}d        e\end{bmatrix}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+f=0}$$
$${\begin{bmatrix}d        e\end{bmatrix}\bm{P}=\begin{bmatrix}d'        e'\end{bmatrix}}$$とする
　$${\begin{bmatrix}\lambda_1x'   \lambda_2y'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+\begin{bmatrix}d'        e'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+f=0}$$
　$${\lambda_1x'^2+\lambda_2y'^2+d'x'+e'y'+f=0}$$　(11)（$${x'y'}$$の項が無くなった！）

ここで座標系$${\text{Oxy}}$$と座標系$${\text{Ox'y'}}$$の関係を考える。
座標系$${\text{Ox'y'}}$$は座標系$${\text{Oxy}}$$を原点中心に半時計まわりに$${\theta}$$回転したものすると
　$${\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}\cos\theta         \sin\theta\\-\sin\theta    \cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}}$$
よって
　$${\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}\cos\theta         \sin\theta\\-\sin\theta    \cos\theta\end{bmatrix}^{-1}\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}\cos\theta   -\sin\theta\\\sin\theta          \cos\theta\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}}$$
　　　$${=\begin{bmatrix}x'\cos\theta-y'\sin\theta\\x'\sin\theta+y' \cos\theta\end{bmatrix}}$$(12)
(7)と比べると
　$${\bm{P}=\begin{bmatrix}\cos\theta   -\sin\theta\\\sin\theta          \cos\theta\end{bmatrix}}$$(13)である。
(1)に(12)を代入する
　$${ax^2+bxy+cy^2+dx+ey+f=0}$$(1)
　$${a(x'\cos\theta-y'\sin\theta)^2+b(x'\cos\theta-y'\sin\theta)(x'\sin\theta+y' \cos\theta)}$$
　　　　$${+c(x'\sin\theta+y' \cos\theta)^2+d(x'\cos\theta-y'\sin\theta)}$$
　　　　　　　　$${+e(x'\sin\theta+y' \cos\theta)+f=0}$$
　$${ax'^2\cos^2\theta-2ax'y'\sin\theta\cos\theta+ay'^2\sin^2\theta+bx'^2\sin\theta\cos\theta}$$
　　　　$${+(b\cos^2\theta-b\sin^2\theta)x'y'-by'^2\sin\theta\cos\theta+cx'^2\sin^2\theta}$$
　 　　　　　　$${+2cx'y'\sin\theta\cos\theta+cy'^2\cos^2\theta+dx'\cos\theta-dy'\sin\theta}$$
　　　　　　　　　　$${+ex'\sin\theta+ey' \cos\theta+f=0}$$
　$${(a\cos^2\theta+b\sin\theta\cos\theta+c\sin^2\theta)x'^2}$$
　　　$${+\{2(c-a)\sin\theta\cos\theta+b(\cos^2\theta-\sin^2\theta)\}x'y'}$$
　　　　　$${+(a\sin^2\theta-b\sin\theta\cos\theta+c\cos^2\theta)y'^2+(d\cos\theta+e\sin\theta)x'}$$
　　　　　　　$${+(-d\sin\theta+e\cos\theta)y'+f=0}$$
(11)は$${x'y'}$$の係数＝０なので
　$${2(c-a)\sin\theta\cos\theta+b(\cos^2\theta-\sin^2\theta)=0}$$
　$${2(c-a)\dfrac{1}{2}\sin(\theta+\theta)+b\cos(\theta+\theta)=0}$$
　$${(c-a)\sin2\theta+b\cos2\theta=0}$$　(14)
　$${\dfrac{\sin2\theta}{\cos2\theta}=\tan2\theta=\dfrac{b}{a-c}}$$　　$${\theta=\dfrac{1}{2}\tan^{-1}\Big(\dfrac{b}{a-c}\Big)}$$　(15)

(i) $${a=c}$$のとき　(14)より$${b\cos2\theta=0}$$　　$${2\theta=\pm\dfrac{\pi}{2}}$$　　$${\theta=\pm\dfrac{\pi}{4}}$$
(ii) $${a\neq c}$$のとき　(15)より$${\theta=\dfrac{1}{2}\tan^{-1}\Big(\dfrac{b}{a-c}\Big)}$$

以上をまとめると
座標系Oxy　　$${ax^2+bxy+cy^2+dx+ey+f=0}$$(1)
　　↓　　半時計方向に$${\theta}$$回転
   　 ↓　　$${\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}   \cos\theta      \sin\theta\\-\sin\theta    \cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\bm{P}^{-1}\begin{bmatrix}x\\y\end{bmatrix}}$$
座標系Ox'y' 　$${\lambda_1x'^2+\lambda_2y'^2+d'x'+e'y'+f=0}$$(11)

３ 具体例

3-1 その１
　$${5x^2-6xy+5y^2-16\sqrt{2}x+16\sqrt{2}y+24=0}$$　(15)

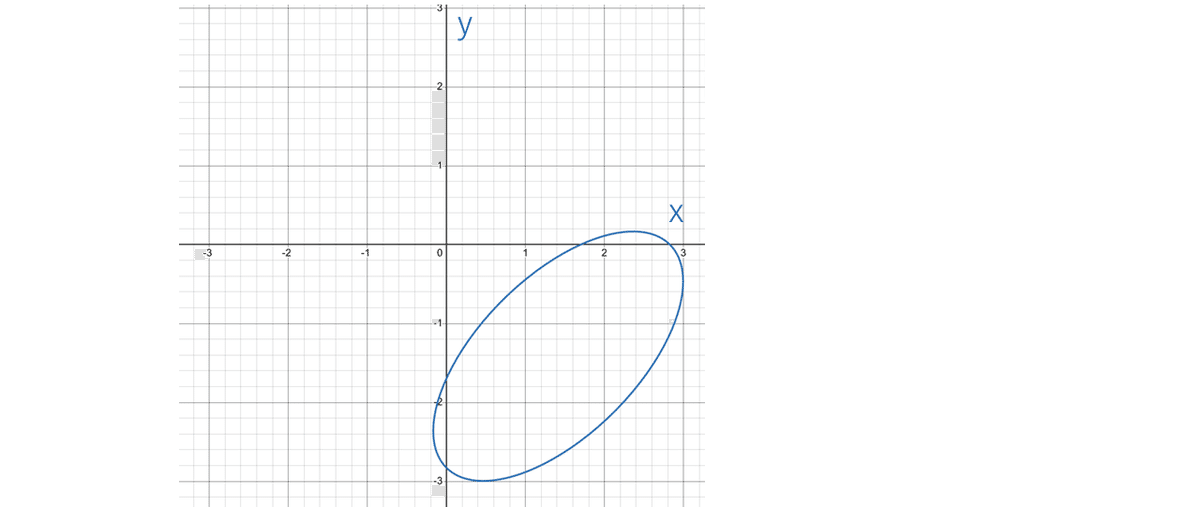
(15)を変形
　$${\begin{bmatrix}x    y\end{bmatrix}\begin{bmatrix}5     3\\3     5\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+16\sqrt{2}(-1     1)\begin{bmatrix}x\\y\end{bmatrix}+24=0}$$　(16)
　$${\bm{A}=\begin{bmatrix}5     3\\3     5\end{bmatrix}}$$
　$${\Big(\begin{bmatrix}5     3\\3     5\end{bmatrix}-\lambda\bm{E}\Big)\bm{x}=\begin{bmatrix}5-\lambda        3\\3        5-\lambda\end{bmatrix}\bm{x}=0}$$　(17)
　$${(5-\lambda)^2-3^3=0           (2-\lambda)(8-\lambda)=0       \lambda_1=2, \lambda_1=8}$$
$${\lambda=2(\lambda_1)}$$のとき
　$${\begin{bmatrix}5-2        3\\3        5-2\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=0        3a_1+3a_2=0}$$
　$${\bm{x_1}=k_1\begin{bmatrix}1\\1\end{bmatrix}        \bm{u_1}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1\\1\end{bmatrix}}$$
$${\lambda=8(\lambda_2)}$$のとき
　$${\begin{bmatrix}5-8        3\\3        5-8\end{bmatrix}\begin{bmatrix}b_1\\b_2\end{bmatrix}=0        -3a_1+3a_2=0}$$
　$${\bm{x_2}=k_2\begin{bmatrix}-1\\1\end{bmatrix}        \bm{u_2}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}-1\\1\end{bmatrix}}$$
よって
　$${\bm{P}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1  -1\\1           1\end{bmatrix}                   ^t\bm{P}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1          1\\1  -1\end{bmatrix}}$$
　※ $${\bm{u_2}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1\\-1\end{bmatrix}}$$も理屈ではありだが、このとき$${\bm{P}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1         1\\1 -1\end{bmatrix}}$$
　　$${=\begin{bmatrix}\cos\theta   -\sin\theta\\\sin\theta          \cos\theta\end{bmatrix}}$$を満たす$${\theta}$$がない。対角成分（$${\cos\theta}$$）は等しく
　　なければならない）
　$${\begin{bmatrix}x\\y\end{bmatrix}=\bm{p}\begin{bmatrix}x'\\y'\end{bmatrix}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1  -1\\1           1\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}\cos(\pi/4)      -\sin(\pi/4)\\\sin(\pi/4)             \cos(\pi/4)\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}}$$
以上を(16)に代入
　$${{^t\begin{bmatrix}x\\y\end{bmatrix}}\bm{A}\begin{bmatrix}x\\y\end{bmatrix}+16\sqrt{2}(-1     1)\begin{bmatrix}x\\y\end{bmatrix}+24=0}$$
　$${{^t\Big\{\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}}\Big\}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+16\sqrt{2}(-1     1)\dfrac{1}{\sqrt{2}}\begin{bmatrix}1  -1\\1           1\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${{^t\begin{bmatrix}x'\\y'\end{bmatrix}}{^t\bm{P}}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+16(-1+1    1+1)\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${{\begin{bmatrix}x'    y'\end{bmatrix}}\begin{bmatrix}2     0\\0     8\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+16(-1+1    1+1)\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${\begin{bmatrix}2x'    8y'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+16×2y'+24=0}$$
　$${2x'^2+8y'^2+32y'+24=0}$$
　$${x'^2+4y'^2+16y'+12=0}$$
　$${x'^2+4(y'+2)^2-16+12=0}$$
　$${x'^2+4(y'+2)^2=4}$$
　$${\dfrac{x'^2}{2^2}+(y'+2)^2=1}$$
新しい主軸系Ox'y'（座標系Oxyを反時計まわりに$${\pi/4}$$回転）で(0, -2)を中心とする長径(x'軸方向)２､短径(y'軸方向)１の楕円である。

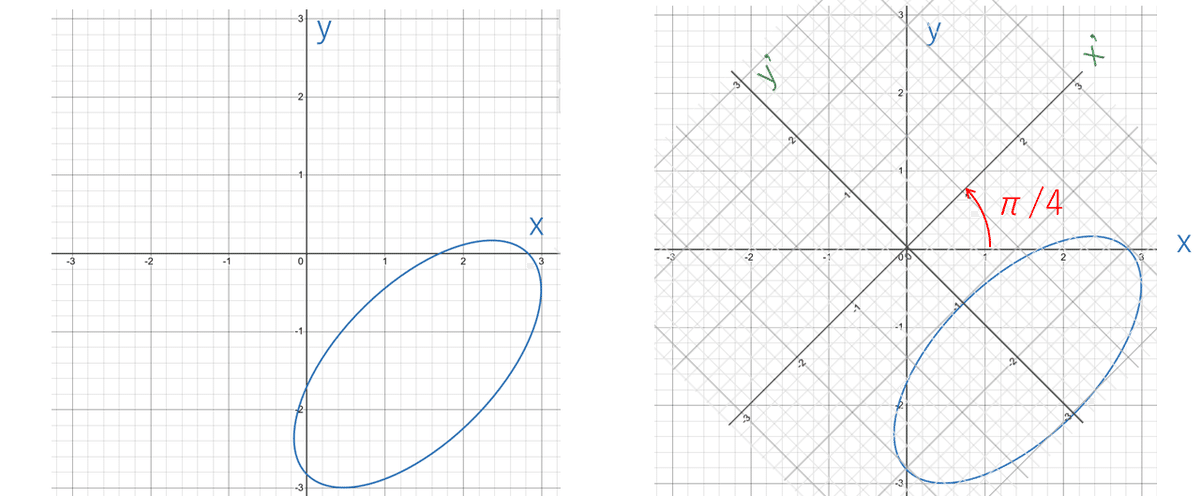
上では$${\bm{P}=\begin{bmatrix}\bm{u_1   u_2}\end{bmatrix}}$$としたが、$${\bm{u_1}}$$､$${\bm{u_2}}$$の順序を入れ替えてみよう。理屈ではありである。
$${\bm{P}=\begin{bmatrix}\bm{u_2   u_1}\end{bmatrix}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}-1     1\\    1       1\end{bmatrix}}$$となるが、対角成分（$${\cos\theta}$$）が等しくない。そこで$${\bm{u_2}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}-1\\1\end{bmatrix}}$$を$${\bm{u_2}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1\\-1\end{bmatrix}}$$としよう。
　$${\bm{P}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}   1     1\\-1    1\end{bmatrix}}$$となる。　$${^t\bm{P}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}1  -1\\1           1\end{bmatrix}}$$　　$${^t\bm{PAP}=\begin{bmatrix}8     0\\0     2\end{bmatrix}}$$
　$${\begin{bmatrix}x\\y\end{bmatrix}=\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}=\dfrac{1}{\sqrt{2}}\begin{bmatrix}   1     1\\-1    1\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}\cos(-\pi/4)    -\sin(-\pi/4)\\\sin(-\pi/4)           \cos(-\pi/4)\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}}$$
これらを(16)に代入
　$${{^t\begin{bmatrix}x\\y\end{bmatrix}}\bm{A}\begin{bmatrix}x\\y\end{bmatrix}+16\sqrt{2}(-1     1)\begin{bmatrix}x\\y\end{bmatrix}+24=0}$$
　$${{^t\Big\{\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}}\Big\}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+16\sqrt{2}(-1     1)\dfrac{1}{\sqrt{2}}\begin{bmatrix}   1     1\\-1    1\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${{^t\begin{bmatrix}x'\\y'\end{bmatrix}}{^t\bm{P}}\bm{A}\bm{P}\begin{bmatrix}x'\\y'\end{bmatrix}+16(-1-1      -1+1)\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${{\begin{bmatrix}x'    y'\end{bmatrix}}\begin{bmatrix}8     0\\0     2\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+16(-2      0)\begin{bmatrix}x'\\y'\end{bmatrix}+24=0}$$
　$${\begin{bmatrix}8x'    2y'\end{bmatrix}\begin{bmatrix}x'\\y'\end{bmatrix}+16×(-2x')+24=0}$$
　$${8x'^2+2y'^2-32x'+24=0}$$
　$${4x'^2+y'^2-16x'+12=0}$$
　$${4(x'^2-4x'+4)-16+y'^2+12=0}$$
　$${4(x'-2)^2+y'^2=4}$$
　$${(x'-2)^2+\dfrac{(y'+2)^2}{2^2}=1}$$
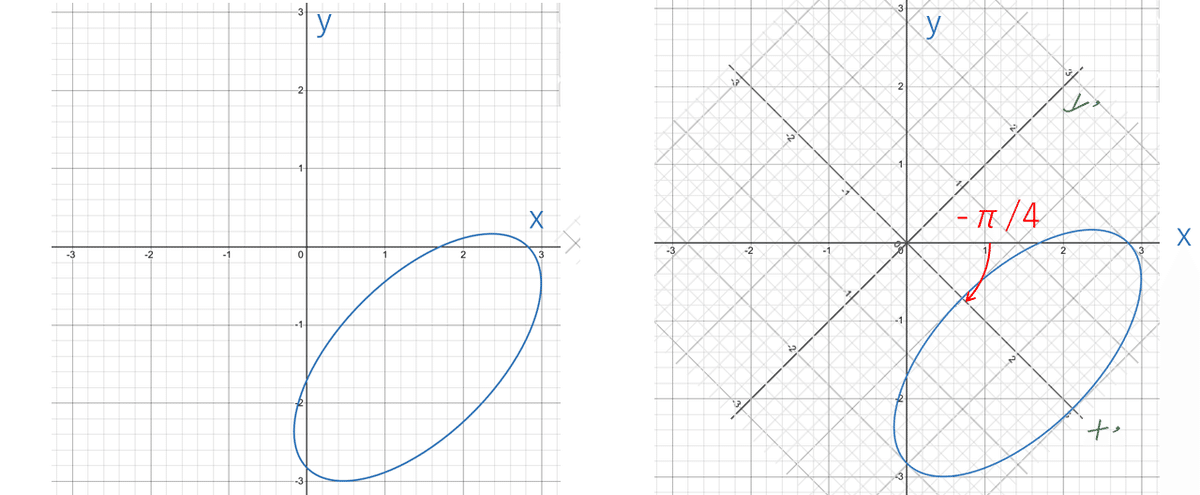
新しい主軸系Ox'y'（座標系Oxyを時計まわりに$${\pi/4}$$回転）で(2, 0)を中心とする長径(y'軸方向)２､短径(x'軸方向)１の楕円である。

以上
双曲線、放物線についても具体例をあげるつもりだったが疲れた。まあこれでよしとしよう。
取りあえず源流のいけるところまでいったということで下流に戻ろう。下流に大きな深みがないことを祈る。あっぷっぷ

追記
グラフの描画にはじめエクセルを使ったが、媒介変数を使ってx､yを出して散布図にした。面倒なので iPadのアプリを探したらf(x, y)=0をそのまま入力したら描いてくれる便利なものが見つかった。どうやってx ,yを求めているのか、まさか裏で主軸変換していることはいないだろうがアルゴリズムに興味が湧く。そのうち調べたい。使ったのは↓のiPad版。便利な世の中になった。

Desmos | グラフ計算機

　　　　　　　　　　　　　　　　　　　→ 力学､物理数学の目次へ