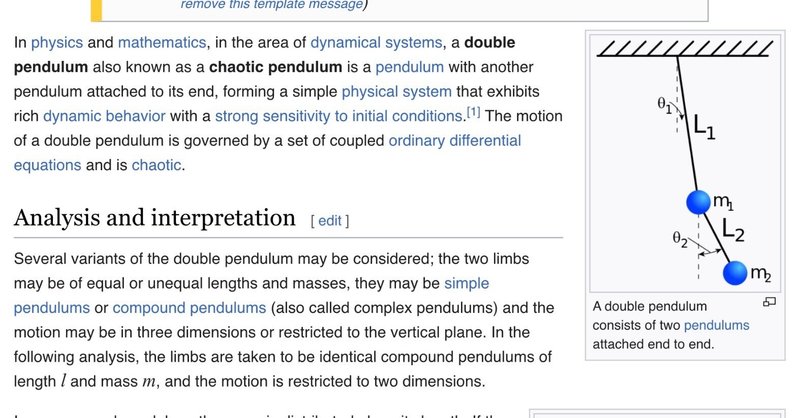
2重振り子
振り子が繋がっている。厄介な設定だがネット上には大量のシミュレーションがあがっている。繋がる振り子の数も2つどころか3つ、4つと。。 実物の動画まである。
ここでは振れ幅(θ、φ)が小さくてマクローリン展開で近似できる場合を考える。

まず$${\mathscr{L}}$$を求めLagrange’s eq に代入する。得られる式は$${\ddot{\theta},\ddot{\phi},\theta,\phi}$$が入り乱れた2元の連立2階微分方程式である$${(①②)}$$。この式を解いても$${\ddot{\theta}=-\omega^2\theta}$$のような都合のよい形にならない$${(③④)}$$。そこで$${\theta}$$と$${\phi}$$をまとめて左辺が$${(〇\ddot{\theta}+\ddot{\phi})}$$、右辺が$${-△(〇\theta+\phi)}$$の形になるように変形する。2通りの変形があり$${(〇=\sqrt{2},-\sqrt{2})}$$、それぞれから得られる連立方程式$${(⑥⑦)}$$を解いて答を得る。

やっと$${〇\ddot{\theta}+\ddot{\phi}=-△(〇\theta+\phi)}$$の形になった! あとは$${(〇\theta+\phi)}$$について解けばよい。

追記
ネットでは行列を使った解き方も散見する。
上記の式①②を行列で表わしたものに逆行列をかけて整理すると
$${\begin{bmatrix}\ddot{\theta}\\ \ddot{\phi}\end{bmatrix}=\alpha\bm{K}\begin{bmatrix}{\theta}\\ {\phi}\end{bmatrix} }$$ ⑧
が得られるが、この式の$${\bm{K}}$$を対角化する。
まず、$${\bm{K}}$$の固有値$${\lambda}$$と固有ベクトル$${\bm{x}}$$、変換ベクトル$${\bm{P}}$$を求める。
($${\bm{K}}$$は$${\bm{P}}$$によって$${\bm{P}^{-1}\bm{KP}=\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}}$$と対角化される)
⑧に左側から$${\bm{P}^{-1}}$$をかけ
$${\bm{P}^{-1}\begin{bmatrix}\ddot{\theta}\\ \ddot{\phi}\end{bmatrix}=\alpha\bm{P}^{-1}\bm{K}\begin{bmatrix}{\theta}\\ {\phi}\end{bmatrix}=\alpha\underline{\bm{P}^{-1}\bm{KP}}\bm{P}^{-1}\begin{bmatrix}{\theta}\\ {\phi}\end{bmatrix}=\alpha\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}\bm{P}^{-1}\begin{bmatrix}{\theta}\\ {\phi}\end{bmatrix}}$$
$${\bm{P}^{-1}=\dfrac{1}{2\sqrt{2}}\begin{bmatrix}\sqrt{2} 1\\\sqrt{2} -1\end{bmatrix}}$$を代入して整理すると
$${\begin{bmatrix}\sqrt{2} \ddot{\theta}+\ddot{\phi}\\\sqrt{2} \ddot{\theta}-\ddot{\phi}\end{bmatrix}=-\alpha\begin{bmatrix}\lambda_1 0\\0 \lambda_2\end{bmatrix}\begin{bmatrix}\sqrt{2} {\theta}+{\phi}\\\sqrt{2} {\theta}-{\phi}\end{bmatrix}}$$
これを崩すと⑥⑦となる。あとは同じ。
この方法は手数が多く煩雑であるが、振り子の数が多い時は非常に有用である。



さらに追記
①②に$${\theta=A\cos(\omega t+B)}$$、$${\phi=C\cos(\omega t+B)}$$を代入し
$${\begin{bmatrix}2\alpha-2\omega^2 -\omega^2\\\omega^2 \alpha-\omega^2\end{bmatrix}\begin{bmatrix}A\\C\end{bmatrix}=0}$$を導く。
$${A=C=0}$$以外の解があるための条件として
$${det\begin{vmatrix}2\alpha-2\omega^2 -\omega^2\\\omega^2 \alpha-\omega^2\end{vmatrix}=0}$$を満たす$${\omega}$$を求め、$${A、C}$$を決定する。


おまけ
以下はシミュレーションと実機での演示である。
この記事が気に入ったらサポートをしてみませんか?
