ベイズ統計学 | 事後分布のサンプリング Importance Sampling

サンプリングが難しい事後分布を近似的にサンプリングするための方法を紹介します．今回はImportance Samplingです．

事後分布$p(\theta | y)$からサンプリングをする方法というより，任意の関数$h(\theta)$に対して以下の$p(\theta |y )$に従う$\theta$に関する期待値を近似する方法です．

$$
\mathrm{E}[h(\theta)] = \int h(\theta)p(\theta | y)d\theta
$$

もちろん，例えば，指示関数$\delta$を用いて$h(\theta) = \delta( \theta < i/N) \quad (\forall i = 1, \dots, N)$と定義すれば累積分布関数は推定できます（$N$は適当に決めた整数で大きければ大きいほど精度が良くなる）．よってDirect Methodでも紹介したように一様分布の乱数から事後分布のサンプリングをすることは可能です．

ここからは正規化されていない$q(\theta | y)$を用いた方法で近似したいとします．

importance sampling

rejection samplingと同様で，サンプリングしやすい適当な$g(\theta)$を用います．

$g(\theta)$を利用して，$p(\theta | y)$に従う$\theta$に関する期待値$\mathrm{E}[h(\theta)]$を$g(\theta)$に従う$\theta$に関する期待値に書き換えます．

$$
\begin{aligned}
\int h(\theta) p(\theta | y) & = \frac{\int h(\theta) q(\theta | y)d\theta}{\int q(\theta|y)d\theta} \\
&= \frac{\int h(\theta)\frac{q(\theta | y)}{g(\theta)}g(\theta)d\theta}{\int \frac{q(\theta|y)}{g(\theta)} g(\theta) d\theta} \\
&= \frac{\mathrm{E}_g\Big[h(\theta)\frac{q(\theta | y)}{g(\theta)}\Big]}{\mathrm{E}_g \Big[\frac{q(\theta | y)}{g(\theta)}\Big]}.
\end{aligned}
$$

ただし$\mathrm{E}_g$は$\theta \sim g(\theta)$に関する期待値を表す．これらの期待値は$g(\theta)$からサンプリングした$\theta^s$を用いて，

$$
\frac{\mathrm{E}_g\Big[h(\theta)\frac{q(\theta | y)}{g(\theta)}\Big]}{\mathrm{E}_g \Big[\frac{q(\theta | y)}{g(\theta)}\Big]} \approx \frac{\sum_s h(\theta^s) \frac{q(\theta^s|y)}{g(\theta^s)}}{\sum_s \frac{q(\theta^s|y)}{g(\theta^s)}}
$$

と近似できる．importance weightを$q(\theta^s|y)/ g(\theta^s)=w(\theta^s)$とおくと，

$$
\frac{\sum_s h(\theta^s) w(\theta^s)}{\sum_s w(\theta^s)}
$$

とかける．

それでは前回の例でも使ったベータ分布のサンプリングをimportance samplingで行ってみよう．

Rによる実践

目標分布を$\text{Be}(8, 6)$としよう．

$g(\theta)$を$[0, 1]$の一様分布とします．

変数$C$は非正規化した分布を構築するために使ったものです．

$N$は累積密度関数の近似計算をするときに使いました．

a <- 8
b <- 6
n.sims <- 1000000
C <- 83
N <- 1000

# sample from uniform distribution
theta.sim <- runif(n.sims)
# calculate weights
w <- C * dbeta(theta.sim, a, b) / 1.0 

cdf <- 0
for (i in 1:N) {
 cdf[i] <- sum(w[theta.sim < i / N]) / sum(w)
}
plot((1:N - 0.5) / N, cdf, xlab = 'p', ylab = 'Pr(P < p | y)', type = 'l', lwd = 2, main = "Example of importance sampling for Beta distribution")
curve(pbeta(x, a, b), xlab = 'p', ylab = 'Pr(p < p | y)', add = TRUE, col = 2, lty = 2, lwd = 2)​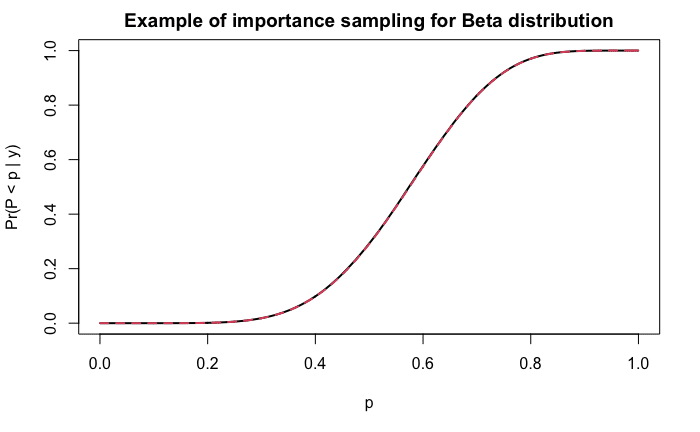

黒い線が近似した累積密度関数で，赤い線が実際にベータ関数の累積密度関数ですが，ほぼ完全に一致しています．