
Mendelian Randomization勉強日記 5. 操作変数のまとめ
mendelian randomization
methods for causal inference using genetic variants chapter 3の勉強まとめ
Mendelian Randomizationを”MR”と略します。
操作変数の妥当性に関する問題のまとめ
・Mendelian Randomizationにおいて操作変数の妥当性は極めて重要
・操作変数の妥当性はできれば生物学的知識に基づいて検証されるべき (統計的にも検証すべきだが)
・イギリスの研究によると、献血者と一般集団の代表で遺伝的バリアントの分布と環境要因などの非遺伝的な要因の分布を調べたところ、環境要因と比較すると遺伝的バリアントの分布は偏りがなかった →一般的には遺伝的バリアントが操作変数として妥当性を満たしやすいことが示唆されるが、特定の研究においては操作変数の妥当性は検証されるべき
ランダム変数としての操作変数の定義 (数学的な定義)
Y: アウトカム, Outcome
X: 要因 (暴露), Exposure
U: 交絡因子, Confounder (often unmeasured)
G: 操作変数, 遺伝的バリアント Genetic variant as an instrumental variable
とおく。
操作変数の定義を再度掲げると
1) GはXと独立でない $${ G \not\!\perp\!\!\!\perp X }$$
2) GはUと独立である $${ G \perp\!\!\!\perp U }$$
3) GはX, Uと条件付けたときにYと独立である $${ G \perp\!\!\!\perp Y| X, U }$$
これは下記のDAGと対応する
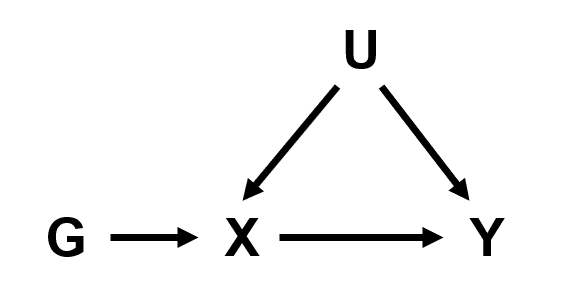
よくある間違い
3番目の仮定を "GはXを条件づけたときにYと独立である ($${ G \perp\!\!\!\perp Y| X }$$ と考えてしまうこと
Xを条件づけると, G→X→Yはblockされるが, G→X←Uのcollider pathが開くので, G→X←U→Yというpathを通してGとYは関連するため, GとYは独立ではなくなる
潜在アウトカムとしての操作変数の定義
p (x|g) :G=gのときのXの確率分布
Y (x, g):X=x, G=gと仮定したときの潜在アウトカムY
X(g):G=gと仮定したときの潜在的な暴露の値X
としたとき、操作変数の定義は
1) Relevance:p(x|g) はgの自明でない関数である。すなわち、遺伝的バリアントが暴露と関連している。
2) Exchengeability:$${ X(g), Y(x, g) \!\perp\!\!\!\perp G }$$
すなわち、暴露・アウトカムの潜在的な値は操作変数 (遺伝的バリアント)の実際の値と独立している。操作変数が交絡因子と関連している場合は事実ではない。
3) Exclusion restriction:Y(x, g) = Y(x)
すなわち、操作変数は暴露を通してしかアウトカムに影響しない。
暴露それぞれの値に対して、counterfactual outcomeは遺伝的バリアントの値によらず同じである。
因果関係を検証する
Mendelian Randomizationでは主に2種類のResearch Questionに答えることができる。
1. 暴露とアウトカムの間に因果関係があるか?
2. 暴露とアウトカムの間の因果関係の大きさは?
(定量化するときの課題もあり、主には1. の疑問に答えるのに適している)
遺伝的バリアントが妥当な操作変数である場合、GとYの間に関連があれば、XとYの間に因果関係があることが示唆される。
観察されたデータで因果推論する
Mendelian Randomizationのような自然実験においては、介入や暴露の操作は行われない。
このため、遺伝的バリアントがアウトカムに与える影響が、同じ暴露の変化を与える(潜在的な)介入を行った場合にアウトカムに与える影響と同一であるという仮定が必要である。これは因果推論の世界でConsistency assumptionと呼ばれる。
(例) CRPが虚血性心疾患発症に影響するか調べたいとする。CRPを平均的に2下げるような遺伝的バリアントがあったとすると、そのような遺伝的バリアントが虚血性心疾患の発症に与える影響が、CRPを平均的に2下げるような介入(例:抗IL-6抗体)を行ったときに虚血性心疾患の発症に与える影響と同じであるという仮定をおくことになる。
Consistencyの仮定をおいているので、Mendelian Randomizationは観察研究ではあるが因果効果を評価している。
実用例: Lp-PLA2と虚血性心疾患
Lp-PLA2は虚血性心疾患の潜在的なリスク因子と考えられた。
観察研究で関連があることがよく知られていた。
DarapladibはLp-PLA2を阻害する薬剤として開発された。
DarapladibがLp-PLA2を低下させることは早期の臨床試験で確認されたが、phase 3 trialsでは虚血性心疾患の発症を低下させる効果はなかった。
これらの臨床試験には10億ドルもの費用がかかった。
Lp-PLA2レベルと関連する遺伝的バリアントを用いて、虚血性心疾患の発症との関連をMendelian Randomizationで検証すると、やはり虚血性心疾患との関連はみられなかった。(試験結果に関する実際のfigureは教科書を参照)
このことは、臨床試験を行う前にMendelian Randomizationで因果関係を検証していれば、巨額の費用を投じる前に結果を予測できていたかもしれないということを示唆している。
因果効果を定量化するときに、追加で操作変数が満たすべき仮定
Mendelian Randomizationで因果効果の有無だけでなく、因果効果の程度の定量化を目的とすることがある。この時には操作変数が満たすべき必要な仮定が増える。
仮定: Monotonicity
操作変数が変化することによる暴露の変化は対象の中のすべての個人で同じ方向に働く(増加または減少)。
biallelic SNPの場合、AA, Aa, aaの3種類においてg=0, 1, 2 (AA, Aa, aa)とおいたとすると、潜在アウトカムを用いてMonotonicityの仮定を表記すると
X(g)はgに対して単調増加または単調減少である
すなわち、すべての個人において
X(0) ≧ X(1) ≧ X(2) または X(0) ≦ X(1) ≦ X(2)が成り立つ
ということを意味している。
Monotonicityの仮定において操作変数の推定はLocal Average Treatment Effect (a complier-average causal effect)を表している。
アルコールの代謝因子であるALDH2遺伝子を用いて、アルコール摂取と食道がん発症リスクに因果関係があるか?という疑問をMendelian Randomizationで検証した報告がある。
この例において、野生型ホモ(アセトアルデヒド代謝できる)>ヘテロ>変異型ホモ(アセトアルデヒド代謝できない)の順に飲酒量が減少していれば、monotonicityの仮定を満たす。野生型ホモなのに、(ほかの理由で)全く飲酒しないような人はmonotonicityの仮定を満たさない。このような場合をnon-complierという。
仮定: Homogeneity
対象の中のすべての個人において、暴露がアウトカムに与える因果効果は一定である (effect modificationがない)
例えば、g=0, 1, 2それぞれにおいてeffect modificationがない
Monotonicityの仮定が満たされない場合、homogeneityを仮定して因果効果を推定することができる。
Homogeneityの仮定では因果効果は集団の中で一定であり、Average Causal Effectを表している。
暴露が二値やカテゴリ変数ではなく連続変数のときは、通常Mendelian Randomization[MR]ではアウトカムとの関係が線形であることを仮定においている。(非線形の関係を前提としたMRは高度な手法でさらなる仮定を必要とする。)
Well-defined interventions
例:「BMIを下げると心血管死が減るか?」という疑問はill-definedである。
なぜなら、BMIを下げる介入が明確に定義されていないためである。
BMIはどうやって下げるのか?代謝を上げる?食欲を抑制する?
BMIはどれくらい長く下げるべき?
BMIを下げる介入は誰に行うのか?
ということをしっかり定義しなければならない。
"no multiple versions of treatment"という仮定
暴露がある値であれば、それがどのような過程をたどった変化であってもアウトカムが一定であるという仮定
→MRで満たすことは難しい (遺伝的バリアントの変化と、ターゲットとする薬剤による介入は介入の期間やメカニズムが異なるから)
しかし、これらの仮定が満たされた時どんな因果効果を推定しているのかを慎重に考えることは示唆的である。
この記事が気に入ったらサポートをしてみませんか?
