
蹴りの為の基礎力学(理論編)
【編集・更新記録】
2023/06/07 誤植部分を多数修正しました。(石黒正隆様よりご協力頂きました。心よりお礼申し上げます。)
2023/06/07 Master Lee様より頂いた資料を追加いたしました。ご協力ありがとうございました。
2023/06/30 第三章の執筆を開始しました。
2023/11/11 「2-5 二物体の単振動モデル」を追加しました。
2023/11/20 「3-3 押し蹴りと前蹴りの物理学的な違い」を追加しました。
2023/11/29 「2-13 最小降下曲線」「補講⑤オイラー・ラグランジュ方程式」を追加しました。
2023/12/8 「2-7 打撃のキレの物理学的定義」を追加しました。
0-1 はじめに
私は李元国や崔泓熙といったテコンドーを作った元老達が卒業した大学で物理学を学んだWTテコンドー愛好家の者です。このノートではテコンドーに関係する物理学の知識を基礎から丁寧に書いていきたいと思います。
物理学とは数学を使って自然現象を説明していく学問です。
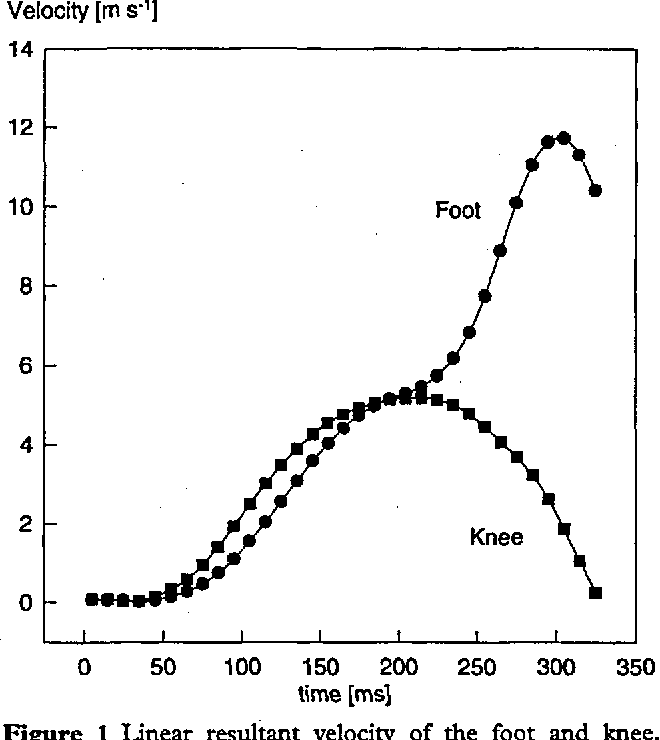
例えば、下のグラフは上段前蹴り中の膝(knee)と足先(foot)の速さの時間変化を表したグラフです。蹴りはじめから200ミリ秒(ms)後までは膝と足首はほぼ同じ速さを持つように加速していき、200ミリ秒(ms)をすこし過ぎたあたりで膝の速さは最大となり、減速を始めていきます。
一方で足先は更に加速していく事から、200ミリ秒(ms)の前後で膝が抱え込まれ、その後に足先が伸びていく事が分かります。
何を言ってるのかさっぱりという方もいらっしゃるかもしれません。このノートでは物理で使われる数学も一つ一つ丁寧にかみ砕きながら説明しています。全く物理学を知らないという人からゴリゴリ理系の大学生までテコンドーを愛する全ての方に物理学を知っていただくきっかけになればと思って、本ノートを書かせていただきました。
0-2 定義という言葉について
物事の意味・内容を他と区別できるように、言葉で明確に限定することを定義と言います。科学的に物事を探究・解析する時には定義が大切で、定義が異なっている人間同士では議論が成り立ちません。詭弁(間違った内容・意見を正しく見せかけたり、自分の意見に言いくるめようとしたりする話し方のこと)のテクニックとして言葉の定義を都合よくコロコロとすり替えるというのがあるように、「定義がちょっとでも曖昧になってくると途中で間違ってくる(苑田尚之)」というのは科学的に物事を考える時には忘れてはいけない視点だと思います。
そして、武術で使われる言葉の定義と科学で使われる言葉の定義は異なる事が多いと言う事も頭に入れておくと良いでしょう。物理学では質量は保存(形態が変わっても総量が変わらない事)しますが、武術において質量は自在に増減します(ITFテコンドーのサインウェーブなど)。これは武術と科学で質量の定義がそれぞれ異なっているからです。
※ 本ノートでは科学で用いられる定義で各種の言葉を用いています。その為、武術的に用いられる言葉と異なる部分が多々あり、違和感を覚える部分も少なくないかもしれません。
科学では言葉の定義を大切にします。「そもそも運動とは何か?」と言われればどう答えるでしょうか? それが科学でなければ、万人がバラバラに思い思いの言葉を使って運動という言葉の意味を説明するでしょう。しかし、それが科学であるならば「時間の変化と共に物体の空間的な位置が変化する事」と万人が同じ答えを答える訳です。
例えば、力という言葉についても同様で、物理学的な意味で力が使われる時には万人が同じ定義を答えなければならない訳です。しかしながら、物理学的な意味での力については強固な誤概念を持つ人が少なくありません。ここでは、一つ一つをかみ砕きながら説明していきたいと思います。
力についての誤概念に対しては、多くの研究や教師の経験では、学習者の 日常経験に発するためであるとしている。しかし、学習後も残る非常に強固な誤概念は、経験よりも寧ろ、観念的な縛りによるものとも考えられる 。

第1章 蹴りの「威力」をどう定義するか?

1-1 力学って何? ニュートンの運動の三法則
自然現象を数学を用いて探求・解析する学問を物理学と言います。
力学とは物理学の一つの分野で、その目的は「物体がいつ・どこにあるかを予測する事」であり、アイザック・ニュートンが作った初頭の力学がニュートン力学です。
ニュートンは一番最初に、その物体の運動を表す量として、運動量を定義しています。物体の質量mと速度vの積を運動量mvと呼ぶことにしました。
また、静止している物体は静止し続けるし、運動している物体も摩擦や空気抵抗などが無ければ速度をそのままに運動し続ける事を実験的事実から発見し、何も無ければ運動量mvは変わらない量であると定義しました。

ニュートンは運動量を変化させる原因を「力」と呼ぶことにし、「1 kg の物体を 1 秒間で秒速 1 m だけ加速させる力を 1 [N(ニュートン)]とする」としました。
ニュートンの決めた力の定義によれば、運動量を変化させる原因が力であり、外から力を受けた物体の運動は変化し、外からの力を受けていないか受けていても合計が0(力のつりあい)になる場合には運動の様子が変化しないという事になります。これを慣性の法則(運動の第一法則)と名付けました。
実は、ニュートン力学で使われる力という物理量を理解する事は地味に難しいと言われています。物理教員向けに書かれた名著「物理を教える」(R.D.ナイト著)の中で、
いったい力とは何か、という問いに対して学生(※著者注:ここでいう学生とは初等の大学物理を学ぶ大学1・2年生の事を指している)は明確な回答を持っていない。力・慣性・エネルギー・仕事率・それに速度さえも区別しないので、しばしばこれらの用語を同じ意味で用いる。
と書かれている様に、「力とは何か」とか「力と運動の関係」とか「2つの物体が相互作用する時にそれぞれ働く力はどのように関連付けられるか」は物理学に慣れない人にとっては難しいものです。ましてや普段から武術・格闘技に触れていて力という言葉を物理学とは全く別の定義で使っていれば尚更です。
では、力と運動の関係について、もう少し掘り下げてみましょう。
先ず、質量$${m}$$[kg]の物体に外から力$${F}$$[N]を加える事で加速させた状態(下図)を考えます。ここで、加速させた時間を$${⊿t}$$[s(秒)]とし、速度の変化を$${⊿v}$$[m/s]とすると、速度は$${v}$$[m/s]から$${v+⊿v}$$[m/s]に加速させたとすると、
$$
F=m\frac{⊿v}{⊿t}
$$
と書けます。運動量(質量×速度)$${mv}$$の変化は$${m⊿v}$$と書ける事から、この式は運動量を変化させる原因が力である事を示しています。
※ ⊿Aや⊿Bなどの⊿をデルタと読みます。一般的に何かの変化量を表す時に物理量を表す文字の前に⊿を付けます。例えば、身長Hに対して⊿Hと書いてあった場合は身長の変化を表します。170cmの人が成長して180cmになった場合は⊿H=10[cm]ですし、その後に加齢とともに178cmになってしまえば⊿H=-2[cm]です。

また、経過時間⊿tや速度変化⊿vを極めて微小な時間dtにおける微小な速度変化dvと置き換えると、下の様な式が成り立ちます。
$$
m\frac{dv}{dt}=F
$$
この式を物理学ではニュートンの運動方程式(運動の第二法則)と呼んでいます。ニュートンの運動方程式から質量mとはその物体の速度の変化しにくさの度合いを表す物理量であることが分かります。同じ大きさの力を加えても質量が高い物体ほど、速度を変化させにくいことが示されます。
また、速度vと位置rの間には次のような関係が成り立ちます。
$$
v=\frac{dr}{dt}
$$
$${\frac{dr}{dt}}$$のように微小な変化量(今回は時間の微小変化dt)で微小な変化量(今回は位置の微小変化dr)を割る事で、ある瞬間(もしくは点)での変化の割合を求める計算を微分と呼びます。上の式は位置を時間微分すると速度が得られる事を示しています。また、その逆の計算として微小な変化量で掛けた物を足し合わせる作業を積分と呼びます。例えば、速度vは位置rを時間で微分する事で得られるので、位置rは速度vを時間で積分する事で得られます。

位置rと速度vの間に成り立つ関係式$${v=\frac{dr}{dt}}$$を運動方程式に適応する事で、
$$
m\frac{d^2r}{dt^2}=F
$$
というような形も得られます。この式は超ミクロな原子レベルの小さな世界を例外とすれば、どんな物体のどんな運動に対しても成り立つ式です。
しかし、初等の物理学で扱う対象は質点(質量を持った点)であったり、剛体(形の変わらない物体)である事が多く、人体の様に常に変形を伴う質量を持った点の集まりについて考えるのは容易ではありません。
何故なら、一本の運動方程式では同じ速度を持った塊に対してしか記述できず、極端な話、蹴りの動作を解析するには蹴りで動く体のパーツの数だけ運動方程式が必要になるからです。
そこで、複数の物体の運動に対して議論する時に重要なのが作用反作用の法則(物体Aが物体Bに力を及ぼす時、物体Bも物体Aに力を及ぼし返し、その大きさは等しく向きは逆になる)です。
例えば、下の図の様な2物体の運動方程式について考えてみましょう。

物体1の質量を$${m_1}$$、位置を$${r_1}$$、物体1が受ける外力の合計を$${F_A}$$とし、物体2の質量を$${m_2}$$、位置を$${r_2}$$、物体1が受ける外力の合計を$${F_B}$$とすると、上図の様に3つの式が立てられます。
(※ 此処で、$${F_{2→1}}$$と$${F_{1→2}}$$は互いに及ぼし合う力(内力)であり作用反作用の関係にあります)

3つの式を変形すると、最終的に二つの物体をまとめた場合の運動方程式に変形することが出来ます。
$$
M\frac{dV}{dt}=F_A+F_B
$$
此処で、Vは2物体の重心座標の速度を表しており、右辺からは互いに及ぼし合う力$${F_{2→1}}$$と$${F_{1→2}}$$が消えています。例えば、人体において筋肉が骨格を引く力が$${F_{2→1}}$$や$${F_{1→2}}$$に相当しており、筋肉による可動が可能な人体であっても外から力を受けなければ重心自体の速度は変化させる事が出来ない事を示しています。
また、2つの物体をまとめた運動方程式を変形すると、
$$
\frac{d}{dt}(m_1v_1+m_2v_2)=F_A+F_B
$$
が得られます。ここで$${m_1v_1+m_2v_2}$$は運動量の総和を意味しており、運動量の和の時間変化は外力によって起きると言う事を意味しています。もし、外から受ける力$${F_A+F_B}$$が無ければ、
$$
\frac{d}{dt}(m_1v_1+m_2v_2)=0
$$
となり、これは外力を受けない系(複数物体のまとまりの事)では運動量の総和が変化しないという事を示しています。これを物理学では運動量保存と呼んでいます。この事は作用反作用の法則が成り立たなければ成立しない事から、運動量保存とは作用反作用の法則を拡張して使いやすくした法則ととらえても良いでしょう。
例えば、跳び後ろ蹴りでは軸足を蹴りとは逆方向の速度で動かす事で蹴り足の速度を速くする事が出来るのですが、これは軸足が負の運動量を持った分だけ、運動量保存の法則から蹴り足の運動量が正の向きに増えたと言い換える事が出来ます。運動量保存の法則は動作を解析する時に非常に有効です。

補講① 時間t・位置r・速度v・加速度a
以下の文章は上記の4つの物理量を整理する為の文章(補講)になります。不要であれば、読み飛ばして下さい。
物理学的な意味での「力」について学ぶことのゴールは、物体がいつ・どこに・どの様な状態であるかを予測する事が出来る様になるという事です。
そこで、まず最初に「いつ」に対応する時刻をtという文字を用いて表すことにします。また、物理では単位も大切です。時刻や時間の単位は一般的に秒を用いてあらわすのですが、秒を意味する英単語(second)の頭文字を使って[s]を用います。
次に「どこに」に対応する位置をrという文字を用いて表すことにします。運動に複数の方向があってそれを分けて決める時はrの代わりにx、y、zという文字を用いて表します。空間上にx軸・y軸・z軸の三方向を定め、その各方向の成分を(x,y,z)で与えてあげる事で物体の位置を指定する事が出来ます。ゲームを作ったりする人がオブジェクトの位置を指定する時などにも用いられます。古いドラゴンクエストなどのRPGは二次元なので、x軸とy軸があれば物体の位置を指定できます。当時の子供たちは「石像から右に5マス、上に6マスの位置に宝があるのじゃ」的なセリフを元に宝を探したりしていました。位置の単位は[m]を使います。かの有名なメートルですが、慣れないうちは質量でよく使われる文字mとゴチャゴチャになりがちです。

例えば、ウサインボルトが走り始めた時刻をt=0[s]、位置をr=0[m]とするならば、ボルトは時刻t=9.58[s]の時には位置r=100[m]を通過することになります。
これが「いつ」と「どこに」という事ですが、「どの様な状態で」という運動の状態について表す為にはどんな物理量を設定すれば良いでしょうか?
では早速考えていただきたいのですが、「運動」って何でしょうか?
最初に物理学は言葉の定義が大事であると言いましたが、運動の定義とは何でしょうか?
ここで読むのを一旦止めて頂いて、30秒ほど考えて頂けたらと思います。
物理学というのはシンプル故に思考が必要な学問になります。間違えてもいいので考えて頂きたいのです。(因みに間違えることはサイエンスの世界では決して悪いことではありません。間違いに気づいて訂正する過程で人類は学んだり新しい発見をしてきました)
運動とは「健康や楽しみのために、体を動かす事。特にスポーツ」と辞書に書いてある様な答え方をされた方。大正解です。大正解なのですが、人間以外のモノの運動の場合はどう答えますか? あるいは体を「動かす」の「動く」とはどういう意味なのでしょうか? 物理学での運動とは「スポーツ」以外の意味を持っています。「運動」って何でしょうか?
さて、ここで運動とは何かを説明する時に、「エネルギーが~」とか、「力が~」とか難しく説明しようとする方も中にはいらっしゃるかもしれません。しかし、出来る限り物事をシンプルに捉えてください。
ここまでこのノートの中で定義がハッキリしている物理量は時間tと位置xだけです。この二つの物理量のみを用いて、運動とは何かを説明が出来ます。
まず、一つが「物体の位置が変わる事」です。例えば、前述のウサイン・ボルトはスタートからゴールまでにx=0[m]からx=100[m]まで位置が変わっています。因みに物理学では変化を表す記号で⊿を用いて、位置の変位を⊿xと書きます。今回のボルトに注目すると、位置の変化⊿x=100[m]です。しかし、その隣のレーンの選手も⊿x=100[m]だし、その隣のレーンの選手も⊿x=100[m]です。時々、小学校の運動会などで張り切ったお父さんが100m走を走るときに、位置x=40[m]くらいで肉離れを起こして途中離脱し、⊿xが100[m]にならないケースもありますが、ほぼすべての世界中の100m走を走る選手たちの位置の変化⊿x=100[m]になります。その選手たちの走りがボルトと同じ運動であると言い切れるでしょうか?
勿論、答えはノーです。タイムが違います。
運動という言葉を説明する為にもう一つ大切な事は「時間の経過」です。時刻t=0[s]に一斉にスタートした選手たちは時刻t=9.58[s]でゴールした選手もいれば、時刻t=10.00[s]でゴールした選手もいます。これを分けて考えなければなりません。
物理学では運動とは「時間の経過に伴って、物体の位置が変化する事」を言います。運動の様子を表す物理量の一つが速度という物理量です。文字はvを用いて単位は[m/s](読み方:メートル毎秒)を用います。日常生活では時速○○キロメートルという表現の方が多く、この場合の単位は[km/h](読み方:キロメートル毎時)となるのですが、物理学では[m/s]の単位を用いる(一般的には秒速○○メートルと表現される)ことの方が多く、この記事でも断りがない限りは速度や速さの単位は[m/s]としたいと思います。
例えば、秒速10メートルという表現が1秒あたり10メートル進む事を意味している様に、[m/s]という単位は、1[s]間に1[m]移動する速さを1[m/s]としています。したがって、速度とは「1秒(単位時間)あたりの位置の変化」と言い換える事が出来ます。
また、これらの前提を元にすると、速度vは時刻の変化(経過時間)⊿tと位置の変化(変位)⊿rを用いて、$${v=\frac{⊿r}{⊿t}}$$と書くことが出来ます。ちなみに速度vの単位[m/s]に注目すると、[(距離の単位)/(時間の単位)]となっており、単位と数式が密接に関係している事がわかると思います。物理では異なる単位を掛け算したり割り算する事が出来ても、足し算したり引き算する事が出来ません。(算数で100000円+5人は意味不明ですが、100000円÷5人なら「10万円を5人で山分けする」と捉えられるのと同じ理屈です)
更にこの速度の式に出てくる⊿tを非常に小さく(dt)してその間に移動した距離⊿r(dr)を測定する事で、その瞬間の速度を求める事ができます(前述した微分$${v=\frac{dx}{dt}}$$の事)。
実際の運動では速度は瞬間瞬間に変化しています。一瞬一瞬で速度が変化する実際の運動について見ていきましょう。

上の図はある運動を解析して、瞬間の速度vを計算して縦軸に速度v、横軸に時間tをとってグラフに表したものです。ここでまた、このグラフがどんな物体の運動を表したグラフなのかを考えてみてください。
縦軸が位置rではなく速度vを表していることに注意すると、時刻t=0[s]の時には物体の速度は0[m/s]であり、最初は止まっている事がわかります。
そこから急激に加速と若干の減速を繰り返して、時刻t=2[s]では速度v=10[m/s]まで加速しているのがグラフから読み取れると思います。更に、グラフ全体がギザギザになっており、この物体が加速と減速を繰り返しているのがわかると思います。ちなみに秒速13メートルは時速46.8キロメートルなので、この物体はt=4[s]以降、原付や公道を走る車並みの速度を持っている事がわかります。
さて、このグラフは何の運動を表しているのでしょうか? もう、お分かりになりましたよね? まだ分からないという方はこのグラフがt=9.58[s]で終わっていることに注目してください。
そうです。
正解はボルトの100m走です。速度が速くなったり遅くなったりを繰り返しているギザギザは歩数に対応します。足でトラックを蹴る瞬間に加速し、足がつく瞬間に若干減速する。ボルトはこれを繰り返して100m走っている訳です。(因みに、このグラフと横軸、縦の直線t=9.58[s]に囲まれた部分の面積を計算すると100mになります。これを速度vを時間tで積分したと言います。)
ここで、「力学」の目的を再確認すると、力学というのは物体が「時刻t」にどの「位置r」に居て、どんな「速度v」を持っているかを予測する為の学問です。「位置r」は「速度v」から分かります。何故なら、速度というのは1秒あたりの位置の変化を表すからです。ある時刻tにおける速度vさえわかれば、未来の位置を予測する事ができます。
では、時刻tにおける位置rを予測するために1秒あたりの位置の変化を表す物理量である速度vが必要な様に、時刻tにおける速度vを予測するためにはどの様な物理量が必要でしょうか?
「1秒あたりの位置の変化が分かれば時刻tの位置rが分かるなら、1秒あたりの速度の変化が分かれば時刻tの速度vが分かるんじゃないの?」
と、即答出来た方、大正解です。時刻tの速度vを知るためには1秒あたりの速度の変化を知る事が必要なのです。そこで、物理学では1秒あたりの速度の変化を表す物理量を加速度と名付けました。文字はaを用いて、単位は速度の変化を時間で割っているので[(m/s)/s]=[$${m/s^2}$$]※(読み方:メートル毎秒毎秒)を用います。
例えば、チーターは走り出してから2秒間で秒速20メートル(時速72キロメートル)に達すると言われて居ます。この時、チーターは1秒あたりの速度の変化(加速度)を計算すると、20[m/s]÷2[s]=10[$${m/s^2}$$
]という数字が得られます。
また、これらの前提を元にすると、加速度aは時刻の変化(経過時間)⊿tと速度の変化⊿vを用いて、$${a=\frac{⊿v}{⊿t}}$$と書く事ができます。
加速度aはこれから本格的に物理の話をしていくときにとても大切な概念になります。何故なら、先ほど、物理学用語の「力」とは物体の運動の様子が変化する(物体の速度が変化する)原因であると説明しましたが、運動の様子が変化するというのはつまり、物体に加速度が生じている状態の事を言うからです。物体に力が働くと加速度が生じると言う因果関係がある以上、加速度という概念が曖昧ならば、「力学」を理解することは難しいでしょう。
ここで、気をつけなければならない事は、位置と速度が違う物理量である様に、速度と加速度もまた異なる物理量であるという点です。加速度という概念を曖昧にしてしまうが為に力学の正しい理解が出来ない方は少なくありません。
ちなみに、物理学では物体が減速していく場合も「加速度が有る」と言います。例えば、摩擦を受けて物体が止まっていく場合は、運動している方向と逆の向き(負の向き)に加速度があるという表現をします。減速する場合でも加速度が有るというのは少しややこしいですが、これも押さえておいてください。
ここまで、変化量を表す記号として、Δを用いて来ました。時刻の変化量であればΔt、位置の変化量であればΔx、速度の変化量であればΔvという様な具合です。しかし、最高速度や最高加速度などは運動の中のほんの一瞬にすぎませんし、アスリートの運動は瞬間瞬間でその速度を変えてしまいます。
したがって、その瞬間の速度や瞬間の加速度を求める為には、Δtを0に近づけるくらい非常に小さくして考えなければなりません。物理学上、非常に小さな変化を扱っている場合はΔの代わりにdを使って表記します(微分)。
例えば、速度v=Δr/Δtという式を書き換えて、v=dr/dtとすれば、このvは0に近い短い時間dtの間にほんの少しだけ移動した位置の変化drの時の速度を意味しており、その瞬間の速度を表しています。
同様に、a=Δv/Δtもほんの短い時間で起きた事を考えるときには、Δをdに置き換えて、a=dv/dtとしてあげれば、瞬間の加速度を表す事ができます。この方程式を解く事で、加速度aから速度vを求める事ができます。
更に、この二つの式を合体させれば、$${a=\frac{d^2r}{dt^2}}と書く事が出来ます。この方程式を解く事で、加速度aから位置xも求める事が出来ます。
加速度の原因となる作用を物理学では「力」と呼んで居るので、「力」について分かれば物体が「いつt」「どこにx」「どんな状態v」で存在するのかを予測する事が出来るのです。
1-2 運動方程式と花山薫方程式
$$
m\frac{d^2r}{dt^2}=F
$$
ニュートンの運動方程式が上式のように示される事は先ほど紹介した通りですが、高校理科などで取り扱われる際は、位置rを時間tで2階微分した量(速度vを時間tで微分した量)$${\frac{d^2r}{dt^2}=\frac{dv}{dt}}$$を加速度aと呼び、
$$
ma=F
$$
と書かれます。
加速度$${a(=\frac{d^2r}{dt^2}=\frac{dv}{dt})}$$は時間に対する速度変化の割合を表しており、重力のみを受ける物体の加速度である重力加速度$${g}$$の値が$${g=9.8[m/s^2]}$$である事は中学理科や高校物理を通して広く知られています。
重力のみを受ける物体(落体など)は1秒あたり9.8[m/s]ずつ速度が変化する事を意味しています。
例えば、9.8×2=19.6[m/s]の速さで真上に投げ上げた物体は1秒あたり9.8[m/s]ずつ遅くなるので、2秒後に速度が0になる瞬間に最高点に達し、その後は2秒間かけて落下し、最終的には下向きに19.6[m/s]の速さを持って落下してきます。

物体の運動を解析する時に難しいのは物理量が非常に多い事です。その物理量が一体何を意味しているのかの定義を曖昧にせずに話をしなければ科学ではありません。
WTテコンドーについて扱われた「跆拳道 韓国の国技」という昭和58年発行の古い本があります。著者の李奎珩先生は後に韓国国技院という韓国テコンドー総本山の理事長となった人物です。本の中に物理学的な視点からテコンドーを説明した次の様な文章があります。
効果的な力と技の使用法は、「力はどのように生成され、どのように発揮され、どのようにして最大の効果を得られるのか」を科学の原理に立脚し、研究することによって初めて生まれるものなのである。
自然界には、重力、弾性力、摩擦力、磁力、電力(著者注:おそらく静電気力の誤訳)、慣性力など、色々な力がある。
ニュートンは、この力を定義する際、運動に伴う質量と速度の変化で力を算出する方式を提案した。
F=m・a(F=力、m=質量、a=加速度)
まず、コチラの記載については大きな誤りはなく、なるほど科学的に話が進んでいくのかと思わせてくれるものです。しかし、そこから続く以下の文章が誤りの宝庫です。この本は確かに素晴らしい先生が書いた本ですが、李師範は物理学は専門外だったらしく、残念ながら物理学に関する間違った記述を並べてしまいました。
この公式は、すべての力を究明する際、非常に便利である。テコンドーにおいても、人間の体重を質量と考え、体や足、拳の動きを加速度とすれば、体重と動作の速度には密接な関係が成立する。
例えば、攻撃を始めるときは、身体は不安定状態(質量の減少、速度の増加)の方が有効であり、防御の場合は、ごく安定した状態(質量の増加、速度の減少)の方が効果的である。が、これではニュートンの運動の法則に一致しない理論が成立する。
この文章は武術的な正しさはあっても、何一つとして物理学的な正しさがありません。例えば、攻撃時の体の不安定さとか防御時の安定という記述は武術的に正しい文章です。(勿論、質量の増減に関する記述は間違っており、物理学的には物体の質量は変わりませんから、括弧内の記述も物理学的には間違いですが、安定と不安定に関しては武術的には正しいと言えるでしょう)にもかかわらず、物理学を誤解している為に「ニュートンの運動の法則に一致しない理論が成立する」と書いてしまったのです。
勿論、李師範が素晴らしい武術家であり、技術論の正しさには疑いようがありませんから、物理学的に正しい説明に書き換え、李師範の武術理論(攻撃時の不安定と防御時の安定)を物理学と一致する事を示していきましょう。
まず、李師範の誤りは加速度と速度を混合して使っている事です。この二つは明確に違う物理量です。更に力についてもニュートンの定義ではなく自分なりの定義に置き換えてしまっています。あくまで、ニュートンは力は加速度の原因だと述べただけで李師範の様に攻撃力や防御力のような曖昧な物を力と呼んだ訳ではありません。
確かに、質量mが大きい物体の速度vが速ければ攻撃の威力が上がります。しかし、それは運動量mvが大きいからであって、運動方程式ma=Fが直接明示する話ではありません。
勝手に加速度aを速度vと読み替えて運動方程式を勘違いする例は少なくありません。加速度を年収だとすると、速度は資産に相当します。年収が高ければ資産も多くなりがちですが、資産と年収はよく似ているけど全く違うものです。
似たような科学的に誤りの多い式で、僕の大好きな方程式があるので紹介させてください。花山薫方程式というグラップラー刃牙という格闘漫画に出てくる理論です。これは、
体重×スピード×握力=破壊力
というものですが、この式に出てくる「×握力」を馬鹿にするニュアンスで運動方程式が用いられ、それも誤った形で紹介される事が多々あり、「どっちも間違ってんだよなぁ」と思う事が何度もありました。

1-2-2 床反力(地面反力)
一般的に人間の運動全体を物理学的に解析するとき、運動方程式$${ma=F}$$の右辺に入るのは地面からの抗力(垂直抗力と摩擦力の合力)と重力になります。物体が外部から物理学的な力を受けている時、重力・電磁気力だけが離れていても物体に対して力を及ぼすことが出来るのですが、それ以外の力は接触している物体から受ける力しかありません。(慣性力や遠心力などは見かけの力なので此処では取り扱わず第二章で説明します)

1-3 作用反作用の法則と衝撃力の力積
花山薫方程式の是非は置いといて、パンチに関する物理学を考察する為に次のようなモデルについて考えてみましょう。
下図のように質量mの物体を速度vで壁にぶつけたところ、速度が0になった状態を設定し、この時に壁が受ける力について計算したいと思います。
この時、壁が受ける力をFとすると、残念ながらこれを運動方程式で直接求めることは出来ません。なぜなら運動方程式とはある物体が外部の物体に与える影響を記述した方程式ではなく、ある物体が外部から力を受けて生じる運動の変化について記述した方程式にすぎないからです。そこで、ぶつかってきた球の運動に注目して運動方程式を立てる必要が出てくるのですが、作用反作用の法則から物体は-Fの力を受けるので
$$
m\frac{dv}{dt}=-F
$$
と書けます。ここでの向きは運動の向きを正としました。
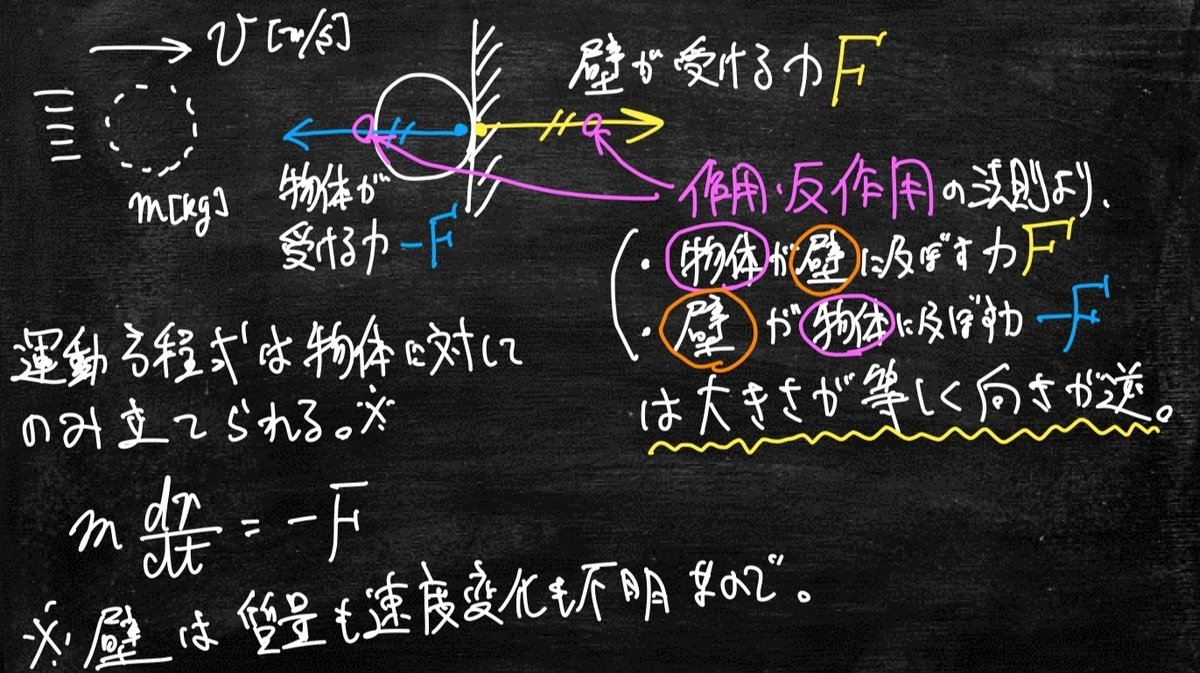
物体に対する運動方程式の右辺が負になると言うことは、左辺の加速度$${a(=\frac{dv}{dt})}$$も負になります。従って、壁に当たった後の拳が減速していくことが示されます。
以下、物体と壁の接触開始をt=0とし、t=⊿tで物体の速度が0になったとし、時間tにおける物体の速度をv(t)、時間tにおける物体が壁に及ぼす力をF(t)と書くことにします。すると、元の式は、
$$
m\frac{dv(t)}{dt}=-F(t)
$$
と書けます。これを両辺をtで積分(t=0からt=⊿tまでを積分区間とする)すると、
$$
\int_{0}^{⊿t}m\frac{d}{dt}v(t)dt=-\int_{0}^{⊿t}F(t)dt
$$
ここで、左辺のみを計算すると、
$$
\int_{0}^{⊿t}m\frac{d}{dt}v(t)dt=[mv(t)]_0^{⊿t}=mv(⊿t)-mv(0)
$$
となります。これは、運動量の変化を表しており、設定された条件よりv(T)=0、v(0)=vとすると、左辺は-mvとなります。これは運動量がmvから0まで変化した時の変化量を表しています。ここから元の方程式は
$$
-mv=-\int_{0}^{⊿t}F(t)dt
$$
が得られます。
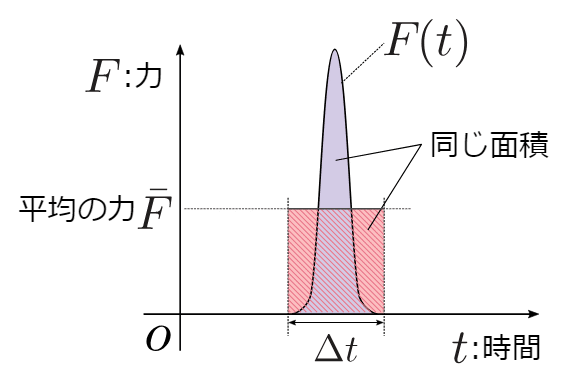
この式の右辺の様に時間変化する力Fを時間tで積分した値は力積と呼ばれています。力の平均値をFとした場合、衝突時間を⊿tとして力積はF⊿tと書く事も出来ます。物体の運動量の変化は物体が受けた力積に等しいという事が示されます。両辺の負号を取り去ると、
$$
mv=\int_{0}^{⊿t}F(t)dt
$$
となり、物体が壁に及ぼす力Fの時間変化をグラフとして書くと下の図のようになります。数式から、グラフの面積が最初に持っている運動量mvと一致する事が分かります。

この事から打撃時に対象に与える力の平均値$${\bar{F}=\frac{mv}{⊿t}}$$は、
・ぶつかる物体の質量(有効質量)mが大きいほど大きくなる。
・ぶつかる物体の速度変化(速度減少)が大きいほど大きくなる。
・接触時間⊿tが短くなれば短くなるほど大きくなる。
という3つの事を示しています。
ここでの質量とは、例えばレスリングやラグビーなどのタックルでは選手の体重全部を質量mと考える事が出来ますが、パンチやキックなどの格闘技の打撃技の場合には全身が打撃に寄与している訳ではありません。打撃に関わる質量を有効質量(Striking Mass)と呼び、有効質量mの値は動作によって変わります。「体重の乗った蹴り」などと言われる蹴りはこの有効質量を大きくした蹴りになります。
また、打撃時に対象に与える力の平均値は工学の世界では衝撃力とも呼ばれています。衝撃力とは質量のあるものが衝突した際に生じる巨大な力の事で、衝撃力は質量と速度が増すことで大きくなり、衝撃で起こる作用が生じる時間⊿tが短ければ短いほど衝撃力は強くなります。
$$
衝撃力:F=\frac{mv}{⊿t}
$$
[接触時間⊿tに関する参考資料]
下のグラフは20代前半で未だ色帯だった頃の私(青帯、-63kg級、東日本選手権二回戦敗退程度)が前回し蹴りをビッグミットに対して蹴った際の足(くるぶし)の速さの時間変化を実際に測定したものです。(z方向が鉛直上向き、y方向が前方向き、x方向は水平方向とし、各成分を足し合わせた最高速度が14.6[m/s]=52.5[km/h]となっています)

そして、この最高速度を迎えた瞬間から速度が0になるまでの部分を拡大すると下のグラフのようになります。この回し蹴りの場合、先ほどの式に出てくる接触時間⊿tは0.02秒~0.024秒ほどの非常に短い時間となる事が分かります。

1-4 2物体の衝突と及ぼし合う力積
ここまではぶつかられる側の物体を壁などの固定された物として想定していましたが、今度は質量Mの静止した物体1に質量mの物体2が衝突した場合についても上記の3つが成り立つのかを考えてみましょう。
互いに及ぼし合う力をfと-fとすると、それぞれの運動方程式は
$$
M\frac{d}{dt}V(t)=f
$$
$$
m\frac{d}{dt}v(t)=-f
$$
と書けます。(ここで物体1の速度はV(t)、物体2の速度はv(t)とした)
2式をまとめると、
$$
M\frac{d}{dt}V(t)=-m\frac{d}{dt}v(t)
$$
となるのですが、左辺はぶつけられた物体1の運動量が増加する割合を意味し、右辺はぶつかった物体2の運動量が減少する割合を意味しています。つまり、衝突によって物体2が失う運動量は物体1に与えられる運動量と等しい事を示しています。
このことから衝突とは運動量を交換する現象といえるでしょう。運動量の変化が衝突による力積(力×衝突時間、$${\int F(t)dt}$$)に等しい事から、やり取りする運動量が多ければ多いほど互いに及ぼし合う力積が大きくなり衝突の規模は大きくなるとも言えます。
具体的に言えば、ぶつかる物体の速度変化(速度減少)が大きければ大きいほど、ぶつかられる物体の速度変化(速度増加)も大きくなり、衝突で及ぼし合う力積が大きくなります。
ここで、二つの物体の反発係数をe(0≦e≦1)として、運動量保存の式と反発係数の式を立て、具体的な力積を計算してみましょう。途中式は省略しますが、下の図のように力積(力と衝突時間の積、F⊿tもしくは$${\int F(t)dt}$$)が得られます(Fは力の平均、⊿tは接触時間)

$$
及ぼしあう力積の大きさ:\int F(t)dt=\bar{F}⊿t=\frac{(1+e)Mmv}{m+M}
$$
に注目して考えてみたいと思います。及ぼし合う力積が質量mによってどう変化していくかを考えます。分母分子をmで割ると、
$$
\frac{(1+e)Mv}{1+\frac{M}{m}}
$$
となり、これにより力積は0<mにおいて単調増加(mが大きくなると、M/mが小さくなるので分母全体が小さくなり、分母が小さくなる事で全体は大きくなる)し、mを無限大にした時の力積の値は$${(1+e)Mv}$$となることが分かります。(また、同様にしてMを無限大にした時の力積の値は$${(1+e)mv}$$となり、反発係数e=0とすると、壁に衝突した時の力積(=運動量の変化量)mvと一致する事が分かります)
質量が重ければ重いほど、速度が速ければ速いほど力積は大きくなります。この式は意外な事に、ぶつけられる側の質量も大きくなれば大きくなるほど力積が大きくなる事を意味しているのですが、作用反作用の法則を考えると妥当と言えるでしょう。
テコンドーという武術を作った元老の一人であるチェ・ホンヒ将軍はテコンドーという武術の中に流れる哲学を一言で言い表すならば柳の様な武術だと語っていました。つまり、風の方向に応じて、自然で柔軟に動き、方向を変える柳のように、テコンドーも状況に合わせて柔軟な思考と攻防を重んじる武術であるという事です。
防御の際も正面からぶつからず、柳の木の様に柔軟に受ける事でぶつけられる部分の質量を小さく出来れば、力積を小さくする事が出来ます。
1-5 打撃力を評価する為に必要な事
しかし、果たしてここで計算していた力積は蹴りの破壊力を評価するのに適切なのでしょうか?
先程も述べた様に力積を大きくするには運動量mv(m:質量、v:速度)を大きく取れば良いのですが、運動量が大きい打撃が強い打撃なのでしょうか?
物理学では力にまつわる物理量として、力に作用時間を掛けた力積F⊿tの他に力を接触面積で割った圧力P(格闘技などで使われる圧力とは全く別の意味である事に注意)という物理量があります。先程の衝突による圧力Pの平均値は衝突部分の面積をSとすると、$${\bar{P}=\bar{F}/S}$$と書けるので、力の平均値$${\bar{F}}$$と圧力$${\bar{P}}$$の平均値は
$$
\bar{F}=\frac{(1+e)Mmv}{(m+M)⊿t}=\frac{(1+e)Mv}{(1+\frac{M}{m})⊿t}
$$
$$
\bar{P}=\frac{(1+e)Mmv}{(m+M)S⊿t}=\frac{(1+e)Mv}{(1+\frac{M}{m})S⊿t}
$$
と書けます。では、打撃力を評価するのには、これらのどの物理量を用いるのが適切なのでしょうか?
極端な例ですが、拳銃から打ち出される銃弾の質量は6.5[g]、拳銃の弾は800[m/s]とするとして、その運動量は僅か約5[kg・m/s]しか有りません。これは5kgの物体が秒速1mで動いている状態と同じ運動量です。
また、プロボクサーのパンチはトップ選手の平均値で時速50km(秒速に直すと14[m/s])であり、打撃の有効質量(striking mass)を腕全体と少なめに見積もって概算して約5kgとしても、その運動量は70[kg・m/s]に達します。その差は14倍にも上ります。打撃力は運動量だけでは決して評価できない事が分かります。
ピストルの弾とパンチがそれぞれ対象に及ぼす力の時間変化のグラフを概形で示すと次のようになります。ここで、運動量の変化はあくまで力積(力と時間の積)に対応する事から、パンチと比較するとピストルの弾はピークの力が大きい代わりに接触時間が非常に短く、グラフの面積は小さくなります。対象に与える運動量が小さい事を考えると、ピストルの弾は身体を突き破る事は出来ても後ろに吹き飛ばす事は出来ない事が分かります。(参考動画:https://www.youtube.com/watch?v=WuxzBNkA8Ws)

1-6 力と変形
物理学分野の力学で取り扱う対象は質量を持った点である質点だったり、大きさがあっても形が変わらない剛体だったりする事が殆どですが、人体は大きさや形を持っており更に変形も伴います。
変形には大きく分けて3種類あります。バネを引っ張った時などの変形の様に形を変えても元に戻る変形(弾性変形)、更に強い力でバネを引っ張った時に元に戻らなくなる変形(塑性変形)、更に強い力で引っ張った時にバネがちぎれてしまう変形(破壊)この三つの変形は外から力を加えた事によります。
物理学で扱う力には、物体の運動状態を変化させる(速度を変化させる)他に物体を変形させるという働きがあります。

例えば、人体に注目すると靭帯が伸びた状態になる事が塑性変形であり、靭帯が切れた状態になる事が破壊です。パンチやキックを受ける時も殆どが表面上には弾性変形ですが、細胞レベルで見ると破壊であり、ダメージは蓄積されていきます。
1-7 変形と応力・圧力
人体の様な大きさと形を持った物体が外から力を受けた時、各人体内部にはその力に抵抗する力(内力)を及ぼし合います。下図のように、壁を力$${F_1}$$で殴った拳がその反作用$${-F_1}$$を受けている状態について考えてみましょう。壁から近い順に人体内部を分割し、各部位の質量を$${m_1}$$、$${m_2}$$、$${m_3}$$、$${m_4}$$……とすると、その各部位は隣り合う部位からそれぞれ下図のように内力を及ぼし合っています。各部位に対して運動方程式を立てると、
$$
m_1\frac{dv_1}{dt}=-F_1+F_2
$$
$$
m_2\frac{dv_2}{dt}=-F_2+F_3
$$
$$
m_3\frac{dv_3}{dt}=-F_3+F_4
$$
$$
m_n\frac{dv_n}{dt}=-F_n+F_{n+1}
$$
となります。壁にぶつかった後の身体の速度は徐々に減速していく事から、各運動方程式の左辺$${m_n\frac{dv_n}{dt}}$$は全て負の値となるので、及ぼし合う内力は右に行くにつれて減衰($${F_n≧F_{n+1}}$$)していきます。

ここで、各部位にはその及ぼし合う内力に応じた変形が生じます。しかし、同じ力を加えたとしても全ての物体で同じように変形するとは限りません。細い物ほど変形しやすく太い物ほど変形しにくい筈です。
この各部位で及ぼし合う内力を断面積で割った値を応力σと呼びます。力を大きくすればするほど、あるいは断面積を小さくすれば小さくするほど応力は大きくなり、物体は変形しやすくなります。
$$
応力σ[Pa]=\frac{内力F[N]}{断面積S[m^2]}
$$
例えば、ハードパンチャーに拳の骨折が多くみられるのは作用反作用の法則から大きな力が反作用として返ってきている為(力が大きい)であり、拳が細い骨で出来ている(断面積が小さい)が故に拳に働く応力が大きくなりがちだからです。

応力同様に力を面積で割った値に圧力(格闘技などで使われる圧力とは全く別の意味である事に注意)という物理量があります。圧力も応力の一種であり同様に[Pa(パスカル)]という単位を用います。物体の表面上に対して及ぼす場合は圧力であり、物体の内部に及ぼす場合は応力と呼んでいます。
$$
圧力P[Pa]=\frac{及ぼす力F[N]}{接触面積S[m^2]}
$$
例えば、押し蹴りや横蹴り、後ろ蹴りの様な蹴りの時に踵のみを突き刺すのと足の裏全体で蹴る場合では及ぼす力の大きさが同じ場合は面積が小さければ小さいほど圧力(単位面積あたりに及ぼす力)が大きくなります。圧力(単位面積あたりに及ぼす力)が大きい蹴りの方がより対象を大きく変形させる事が出来ます。
物体が破壊される直前の応力を破壊応力と呼び、物体に破壊応力を超える応力を加えられた時に物体は破壊(2物体以上に分裂する)されます。したがって、蹴りの破壊力は蹴りによって及ぼされる圧力の最大値を大きくすることで増していく事が分かります。
この事から、これまでの項目で出てきた、
・ぶつかる物体の質量m(有効質量)が大きいほど大きくなる。
・ぶつかる物体の速度変化(速度減少)が大きいほど大きくなる。
・接触時間が短くなれば短くなるほど大きくなる。
という3点にプラスして、接触面の断面積Sを小さくする事(圧力を大きくする)というのが蹴りの破壊力を増す為に重要です。
1-8 エネルギー積分(運動エネルギーと仕事)
今度は、質量mの物体を速さvで壁に衝突させたところ、変形によって衝突後の重心位置が衝突時間ΔTの間にΔxだけ変化したモデルを考えたいと思います(参考URL:https://www.youtube.com/watch?v=AkB81u5IM3I)。
この時、壁と物体が及ぼしあう力を一定値Fと近似できるものとすると、物体の運動量変化と壁から受ける力積の関係からmv=FΔtと書けます。

この間の運動方程式は、
$$
m\frac{dv(t)}{dt}=-F
$$
この両辺に$${v=\frac{dr}{dt}}$$ をかけて時間tで0からΔtまで積分する(この積分計算は両辺の単位がエネルギーの単位である[J(ジュール)]になることからエネルギー積分と呼ばれる)と、
$$
\int^{⊿t}_0mv\frac{dv(t)}{dt}dt=-\int^{⊿t}_0F\frac{dr}{dt}dt
$$
時刻t=⊿tにおける速度v=0、変位r=⊿xである事から、
(右辺のFを一定とみなしたのは計算を簡略化する為です)
$$
\int^{0}_vmvdv=-\int^{⊿x}_0Fdr
$$
$$
[\frac{mv^2}{2}]^{0}_v=-[Fr]^{⊿x}_0
$$
$$
-\frac{1}{2}mv^2=-F⊿x
$$
この式の左辺の$${\frac{1}{2}mv^2}$$は物理学では運動エネルギーと呼ばれるものであり、これが負の値になっている事から、衝突前後での運動エネルギーの減少分を意味しています。また、右辺の-F⊿xは物理学では仕事(以下、一般的な仕事という言葉との誤用を避けるために力学的仕事と呼ぶ)と呼ばれるものであり、物理学では力学的仕事は「エネルギーの移動形態」と考えられています。この式を変形する事によって力Fを求める事が出来るので、
$$
F=\frac{mv^2}{2⊿x}
$$
が得られます。運動量と力積の式からFを求めた物と比較すると、
$$
\frac{mv^2}{2⊿x}=\frac{mv}{⊿t}
$$
此処から、変形による変位⊿xと接触時間⊿tの関係は、
$$
\frac{⊿x}{⊿t}=\frac{v}{2}
$$
となる事が分かります。右辺は速度によって決まる値ですから、接触時間⊿tはぶつかる物体の変形⊿xを小さくする事によって小さくなる事が示唆されています。
例えば、俗にヤクザキックと呼ばれる様な押し蹴りは足が曲がった状態でターゲットに接触した後に相手を押す様に蹴り足を変形させていく事から、変形⊿xが大きく接触時間⊿tが長い蹴りと言えます。したがって、同じ速度を持った前蹴りと比較すると、力の最大値が小さい力を長い時間長い距離加える事になるので、「破壊力※」の劣る蹴りであり相手に効かない蹴りとなってしまいます。
※:ここでは圧力の最大値を「破壊力」と呼ぶとして、足裏の様な接触面積の広い蹴りの場合、余計に相手に効かせにくい蹴りになってしまう。
WTテコンドーの前回し蹴りの場合は足の甲で蹴るのですが、「身体が硬い人の蹴りは痛い」という俗説があります。これは足首が硬い人ほど蹴り足の変形⊿xが少なく接触時間⊿tを短く出来る為でしょう。逆に足首が柔らかい人の蹴りは運動量や運動エネルギーが大きくても足首関節の変形に伴い接触時間が長くなってしまう為、破壊力の劣る蹴りになります。足の甲で破壊力を出そうと思ったら「足首を固めて蹴る」というのが大切ですし、強い蹴りを蹴ろうとして「脛と足首の間を当てる」というのも、変形しにくい部位を当てるという点で有効です。
1-9 力学的エネルギー保存
同じ話の繰り返しですが、物理では力を加えて物体を移動させることを力学的仕事と呼んでいます。一定の力ならば力と移動距離の積で仕事を計算することが出来ますが、力が一定でない場合でも、微小距離drを掛け合わせたものを足し合わせて(rで積分して)仕事の大きさWは$${W=\int F(r)dr}$$として表すことが出来ます。
ここでニュートンの運動方程式、$${m\frac{dv}{dt}=F}$$の両辺をrで積分して、
$$
\int m\frac{dv}{dt}dr=\int Fdr
$$
$$
\int mvdv=\int Fdr
$$
ここで、物体が外から仕事をされる前の速度を$${v_0}$$、物体が外から仕事をされた後の速度を$${v_1}$$とすると、
$$
\int^{v_1}_{v_0} mvdv=\int Fdr
$$
$$
\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2=\int Fdr
$$
という数式が得られ、左辺は質量mの物体が持っている運動エネルギーの変化を意味しており、右辺はその物体に加えられた力学的仕事を意味します。
すなわち、仕事というのはエネルギーの移動形態であり、仕事をされた物体のエネルギーは増えることを意味します。また、この式を逆に考えることもできます。つまり、もしも速度が減少している($${v_0>v_1}$$)ならば運動エネルギーの減少分が仕事と等しくなり、エネルギーとはその物体が潜在的に持つ外部に力学的仕事をすることのできる量であることを示していると読み取ることもできます。
エネルギーを持った物体はそのエネルギーの減少分だけ外部に仕事をすることが出来るのです。
重力mgを受ける質量mの物体に対してそれに逆らう力Fを加えて静かに動かした場合の運動方程式を考えてみましょう。右辺に重力を付け足して、
$$
m\frac{dv}{dt}=F-mg
$$
ここで、ゆっくり動かした場合に速度変化dvはゼロになるので、左辺は0となりますから、$${0=F-mg}$$となり、$${mg=F}$$が得られます。これをrで積分することで、力Fの仕事を求めたいと思います。物体の最初の高さをh、仕事を受けた後の高さをHとすると
$$
\int^H_hmgdr=\int Fdr
$$
$$
mgH-mgh=\int Fdr
$$
ここで、左辺のmgHは力学的仕事を受けた後に持っている何らかのエネルギーであり、mghは仕事を受ける前に持っている何らかのエネルギーを意味しており、この左辺は仕事を受けたことで増えた何らかのエネルギーの変化を示しています。このように、高いところにある物体は何らかの形でエネルギーを持つことが示されており、このエネルギーを(重力による)位置エネルギーと呼び、位置エネルギーは重力mgを用いてmghと書くことが出来ます。
位置エネルギーmghと運動エネルギー$${\frac{1}{2}mv^2}$$の和を力学的エネルギーと呼んでいます。また、物体が摩擦力や垂直抗力などの力の仕事を受けなければ力学的エネルギーの総量は変わりません。これを力学的エネルギー保存の法則と呼んでいます。ただし、摩擦や垂直抗力が力学的仕事をした場合でも、力学的エネルギーがほかの形のエネルギー(化学エネルギーや熱エネルギーや音エネルギーなど)と変形しあいながら出入りするだけであり、エネルギーの総量自体は変わりません(エネルギー保存の法則)。
例えば、摩擦力が負の仕事をして運動エネルギーを0にしたとき、その失われた運動エネルギー分だけ熱エネルギーに変換され物体の外部に放出されます。
力学的エネルギー保存の法則が成り立つ例として、質量mの物体を1m(※単位のメートルであって質量のmとは別物です。間違えることはないと思いますが念為)だけ物体を落下させる場合について考えてみましょう。失われた位置エネルギーはmgh=m×9.8×1[J]になります。変換された運動エネルギーとの間で等式を結ぶと、
$$
\frac{1}{2}mv^2=m×9.8×1
$$
両辺をmで割ると、mを消去することが出来るので、速さvは高さhと重力加速度g=9.8のみで与えられ、質量には無関係であることが分かります。
$$
v=\sqrt{2×9.8×1}≒4.43[m/s]=15.9[km/h]
$$
また、この計算を用いて、自由落下(初速度0で鉛直に落下する運動)の落下距離・落下時間・速さの関係は次のような表を作ることが出来ます。
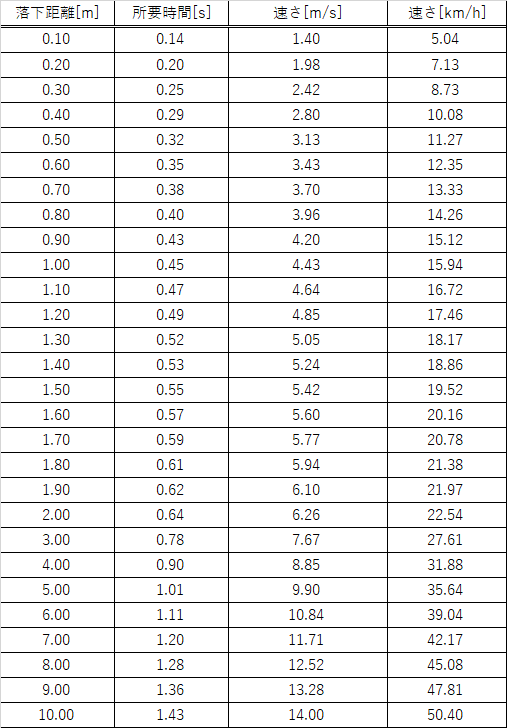
一般的にボクサーのパンチのトップスピードは時速50㎞と言われているが、これは10mの高さから物体を落として位置エネルギーをすべて運動エネルギーに変換させたときに匹敵する速さであることが分かります。
他の例として、踵落とし(ネリョチャギ)は位置エネルギーを運動エネルギーに変換する蹴りと思われがちだが、ネリョチャギの落下距離を0.5mと仮定しても、その速さは僅かに時速11km程にしかならず、実際には位置エネルギーの影響は0ではないが、それほど大きくないこともわかります。
また、0.4mと10mを比べると、位置エネルギーの差は25倍だが速度の差は5倍にしかならない。これは運動エネルギーの式($${\frac{1}{2}mv^2}$$)の中で速度が2乗になっているためであり、速度が増えれば増えるほどそれ以上に速度を増やすために必要なエネルギーが増えていきます。
実際に赤帯くらいの選手とトップレベルの黒帯の選手の蹴りのスピードを測定してもその差は意外なほどに小さくなってきます。すでに十分にスピードを持っている選手がそれ以上に速さを獲得することの困難さを運動エネルギーの式は示しています。

とはいえ、人体の動作において、力学的エネルギーが保存する例は非常に稀です。というのも、筋肉が収縮するときには生体内のエネルギー供給減であるATP(アデノシン三リン酸)というものを分解して化学エネルギーを運動エネルギーに変換しているからです。つまり、力学的エネルギー以外のエネルギーである体内に蓄えられた化学エネルギーが筋収縮(筋力発揮)を介して力学的エネルギーへと変換されているのです。
1-10 エネルギー生成と伝達
それでは、人体内でどのようにして運動エネルギーが生成されるかを考えてみたいと思います。物理学的には「静止した物体を運動させるには外から力を加えなければならない」とされています。これが有名なニュートンの運動の法則ですが、我々動物にも適応される話と言えるでしょうか?
外から力など受けなくとも、腕を曲げようと思えば曲げられますし、足を伸ばそうと思えば伸ばせますから、我々動物はニュートンの運動の法則の外側にあるかのような気がしてきます。
確かに、我々の身体をパーツごとに区切ってみてみれば、ニュートンの運動の法則に従う事は間違いありません。肘関節を曲げられるのは、筋肉の収縮に伴う張力で骨が引っ張られているからであり、骨を筋肉が引っ張る反作用が筋肉を逆向きに引っ張っています。急激な運動によって筋肉が断裂する肉離れが起きるのがその証拠です。
物理学を学ぶときに基本中の基本である力学的エネルギー保存は人体の動作において大抵の場合で成り立ちません。
力学的エネルギー保存とは物体に保存力(重力や弾性力や静電気力)のみがはたらく場合、その物体の力学的エネルギーは一定になるのですが、筋収縮によって生じる張力は保存力ではありません。筋収縮に伴って筋肉が骨格に対してする力学的仕事(力と作用点の移動距離の積の事)は運動エネルギー(あるいは位置エネルギー)へと変換されています。このエネルギーは元々は筋肉を構成する細胞に蓄えられた化学エネルギーであり、筋肉の仕事を介して運動エネルギーへと変換され続ける訳です。人体の動作において力学的エネルギーが決して保存しない(一定にならない)のはその為であり、人体の運動において運動エネルギー(あるいは位置エネルギー)は絶えず化学エネルギーを元にして生成され続けています。そして、その化学エネルギーは食物を消化・吸収して筋肉に蓄えたグリコーゲンなどの栄養に由来するエネルギーになります。我々動物は自分の体内に蓄えた化学エネルギーを自由に引き出して運動エネルギーへと変換する事が出来るという点で物理学で扱われるような単純な物体とは異なるのです。
例えば、机の上に重りを乗せた場合、重りは外からエネルギーを加えなくてもその高さに居続ける事が出来るのですが、僕らが重りを手に持って支える場合には僕らのエネルギーは絶えず消費され続けます。勿論、どちらも重りが持っている位置エネルギーが変わらないという点では同じです。違いは僕らの筋肉は同じポーズを取り続ける為にも絶えず筋収縮と弛緩を繰り返さなければならないという点にあります。筋肉をミクロな視点で見た時には絶えず、筋繊維は外に対して力学的仕事をしています。この力学的仕事によって筋肉は化学エネルギーを筋肉の収縮に伴う運動エネルギーへと変換し、それは最終的に熱エネルギーへと変換されていきます。
筋肉で生成された運動エネルギーは関節力による仕事を介して人体内を移動します。このようなエネルギー伝達の流れをエネルギーフローと呼びます。例えば、回し蹴りなどの打撃動作を運動エネルギーという観点で議論する場合、より多くの筋肉を利用して運動エネルギーを作り出し、更にはそれを無駄なく蹴り足まで伝達できる動作を良い動作(良いフォーム)として評価する事が出来ます。一方で、エネルギーを生成する筋肉が少なかったり、生成したエネルギーが伝達する過程で大きなエネルギーロスが生じる動作を悪い動作(悪いフォーム)と評価する事が出来るでしょう。
良い蹴りとは何かと問われれば、物理学的には「多くの筋肉がエネルギーを生成し、それを効率よく蹴り足の運動エネルギーに変換できる蹴り」と説明する事が出来ます。
例えば、打撃の際には床を踏む事が重視される事があります。床を踏む事で軸足を含む身体の一部分が固定され、筋肉が生成した運動エネルギーが打撃部位以外に流れていく事を防ぐ働きがあります。
補講② ベクトルの合成と分解
位置$${\vec{r}}$$、速度$${\vec{v}}$$、加速度$${\vec{a}}$$、力$${\vec{F}}$$の様に向きを持った物理量の事をベクトルと呼びます。ベクトルである事を強調する際には文字の上に→を書くか、もしくは$${\bm{F,a,v,r}}$$の様にボールドイタリック体で示します。本ノートでは$${\vec{a}}$$という形式で書きたいと思います。
ベクトルが向きを持たない物理量(スカラーと呼ぶ)と異なる点としては、1+1=2が成り立たない事がある点です。例えば、質量1[kg]の物体と同じく質量1[kg]の物体を足し合わせた質量は絶対に2[kg]になるが、力1[N]と力1[N]を足し合わせた場合、2[N]になる事もあれば0[N]になる事もあります。

位置ベクトル$${\vec{r}}$$を二方向x、yに分解した成分は下図のように書く事が出来て、それぞれの方向の成分を用いて$${\vec{r}}$$=(x,y)とも表記します。ここで、位置ベクトルの長さをrとすると、三角比sinθ、cosθを用いてx=rcosθ、y=rsinθであり、$${\vec{r}=(rcosθ,rsinθ)}$$と書けます。
力学では斜め方向のベクトルをx方向とy方向に分解して、各方向で分けて考える事で現象をシンプルに捉える事が出来ます。

1-11 力学的波動と単振動
物体の一部分を振動させると、それにつながった別の部分も振動を始めます。このように一か所の動きが別の部分に伝わっていく現象を物理学では波動と呼んでいます。スピリチュアルやオカルトの世界でも波動という言葉は好んで使われていますが、物理学における波動とは単に振動が次々と伝わっていく現象のことを指しています。
例えば、顔面にボールがぶつかったときの様子をスーパースローで撮影すると、ボールがぶつかった事で頬→鼻と唇→逆の頬と振動が次々と伝わっていき、顔の各パーツがボールの運動と同じ方向に振動しているのが分かります(参考URL:https://www.youtube.com/watch?v=XjwO9InuFJk)。このような振動が伝わっていく現象を波と呼んでいます。
すなわち、打撃が体の表面に当たってから体の内部にある内臓まで影響を与えるのも、打撃に起因する波動が身体の内部を伝わるからであり、衝撃の伝わり方を学ぶためには波動について学ぶことが大切になります。

波動とは振動が次々伝わる現象ですが、最もシンプルな波動を正弦波(サインウェーブ)と呼び、その各点の振動のことを単振動と呼んでいます。
ITFテコンドーでは身体の重心で正弦波(サインウェーブ)を描くような動きが突きや受けには用いられています。その為、物理学で扱われる力学的波動と混同されやすくなりがちですが、「サインウェーブによる突き」では重心が正弦波を描きながら前に進んでいきますが、力学的波動の場合は媒質の各点は元々の位置を中心にして振動しているだけで、波と共に進んでいく訳ではありません。
波には媒質(波を伝える物質の事)の振動方向によって縦波と横波の二種類に分けられます。例えば、人体へ伝わる衝撃が体内を伝わっていくときは、圧縮が次々と伝わっていく縦波であり、体の表面を伝わっていく様な波は横波になります。波が伝わる速さは縦波の方が速いため、地震波では先に縦波が到着し(初期微動)、そのあとで横波が到着します(主要動)。地震の際に最初に横揺れ(縦波)が来てそのあとで縦揺れ(横波)が来るというのは下の図を見ると想像しやすいでしょう。

縦波は圧縮された点(密)と拡張された点(疎)が次々と伝わっていく波なので、疎密波とも呼ばれています。例えば、打撃によって生じる波は連続波ではなく、密一個が次々と伝わっていくような半個分の波と考えることが出来ます。また、縦波の伝搬速度はヤング率(物体の変形しにくさの度合い)が大きければ早くなり、密度が高ければ遅くなるという性質があります。
それでは、各点の振動について考えてみましょう。位置rが時間tの関数として表す事が出来、振幅A(振動中心から端までの距離)、角振動数ω、初期位相αを用いて、
$$
r(t)=Asin(ωt+α)
$$
と書く事が出来る運動の事を単振動と呼んでいます。これを時間tで微分して速度vを得ると、
$$
v(t)=\frac{dr}{dt}=Aωcos(ωt+α)
$$
となり、更にもう一度時間tで微分して、加速度aを得ると、
$$
a(t)=\frac{d^2r}{dt^2}=-Aω^2sin(ωt+α)=-rω^2
$$
が得られます。つまり、単振動する物体の位置r(t)は角振動数ωを用いて、
$$
\frac{d^2r}{dt^2}=-ω^2r
$$
という方程式が成り立つ事になります。また、一回振動する時間(周期)をTとすると、sinを定義する動径が一周した時の角度が2πとなる事から、角振動数ωとTの間にはωT=2πという関係が成り立っています。
例えば、バネでつながれた物体の振動や浮力を受けて水面に浮かぶ物体の振動などは$${\frac{d^2r}{dt^2}=-ω^2r}$$を満たす事が知られており、単振動の例として物理学では取り扱われています。フックの法則(バネが変形した時に自然長からの変位とバネが他の物体に及ぼす弾性力が比例するという法則)に従うバネに質量mの物体を繋いで単振動した場合、運動方程式は、
$$
m\frac{d^2r}{dt^2}=-kr
$$
となります。ここで、位置rはつりあいの位置を原点とした物体の位置とし、kは物体につないだバネ定数(単位[N/m])であり、$${\frac{d^2r}{dt^2}=-ω^2r}$$と比較すると、
$$
ω^2=\frac{k}{m}
$$
が得られ、$${ω=\sqrt\frac{k}{m}}$$となるので、周期Tは
$$
T=2\pi\sqrt{\frac{m}{k}}
$$
となります。バネ定数kはバネの硬さに対応する定数であり、これにより単振動の周期は質量が重いほど長くなり、バネが硬くなるほど短くなる事を示しています。また、速度$${v(t)=Aωcos(ωt+α)}$$の式より、振動の速さは角振動数ωが大きくなるほど速くなり、$${v(t)=A\sqrt{\frac{k}{m}}cos(\sqrt{\frac{k}{m}}t+α)}$$と時間と共に変化し続けるが、その最大値は
$$
v_{max}=A\sqrt{\frac{k}{m}}=A\frac{2\pi}{T}
$$
となり、単振動する物体の速さは繋がった物体のバネ定数kが大きいほど、物体の質量が軽いほど、速くなることが分かります。さらに、1秒当たりの振動回数(周波数)f[Hz]と1回の振動にかかる時間(周期)T[s]は逆数の関係($${T=\frac{1}{f}}$$)にあるので、
$$
v_{max}=2{\pi}Af
$$
ここで、運動エネルギーは$${\frac{1}{2}mv^2}$$なので、単振動する物体の持っているエネルギーは、
$$
\frac{1}{2}mv^2_{max}=\frac{1}{2}m(2{\pi}Af)^2=2\pi^2mf^2A^2
$$
となるので、単振動が持つエネルギーは振動数fが大きければ大きいほど、振幅Aが大きいほど、質量mが重いほど大きくなる事が分かります。力学的波動という物理現象は、この単振動が持っているエネルギーが次々と伝わっていく現象とも説明する事が出来ます。
1-12 打撃を単振動でモデル化する
例えば、打撃における拳や足などの衝突する物体を弾性体(非常に硬いバネの衝突)とみなし、衝突において壁に及ぼす力の平均値$${F}$$を考えたい。

弾性体が縮む現象は単振動として考える事が出来るので、速度$${0}$$から速度0になるまでの時間は、単振動の1/4周期になるので、
$$
t=T/4=\frac{π}{2}\sqrt{\frac{m}{k}}
$$
と書けます。また、質量$${m}$$で速度$${v}$$の物体の速度が0になるまでの運動量の変化が力積と等しい事から、
$$
-mv=-Ft
$$
が得られ、物体が壁から受ける力は、
$$
-F=-\frac{mv}{t}=-\frac{2v}{π}\sqrt{mk}
$$
となります。したがって作用反作用の法則から、衝突した物体が壁に及ぼす力の平均値(衝撃力とも呼ばれる)Fは
$$
F=\frac{2v}{π}\sqrt{mk}
$$
と書けます。ここで、運動エネルギー$${E=\frac{1}{2}mv^2}$$を変形して代入すると、
$$
F=\frac{2}{π}\sqrt{2kE}
$$
が得られ、衝突により壁に及ぼす力の平均値(衝撃力)Fが運動エネルギーEとバネ定数kによって決まる事が分かります。ここで、バネ定数とはバネを1m縮めるのに必要な力の大きさを表しており、バネの変形しにくさを示しています。
したがって、打撃を単振動でモデル化して議論した場合、運動エネルギーの他に、衝突する物体の硬さ(変形しにくさ)も打撃によって及ぼす力を評価する為に必要である事が分かります。

また、打撃の破壊力を決めるのは圧力の最大値である事から、圧力の最大値と運動エネルギーの関係について考えたいと思います。
打撃の変形を単振動とみなした場合、質量$${m}$$で速度$${v}$$の物体の速度が0になるまでの速度の変化は、
$$
v(t)=vcos\sqrt{\frac{k}{m}}t
$$
また、衝突する物体が受ける力の大きさは、運動方程式$${m\frac{d}{dt}v(t)=F}$$よりv(t)を時間微分した値にmを掛けた物に等しく、これを計算すると、
$$
m\frac{d}{dt}v(t)=-mv\sqrt{\frac{k}{m}}sin\sqrt{\frac{k}{m}}t
$$
となり、壁が受ける力はこの反作用なので、
$$
F(t)=mv\sqrt{\frac{k}{m}}sin\sqrt{\frac{k}{m}}t
$$
が得られる。この最大値は運動エネルギーEを用いて、
$$
F_{max}=v\sqrt{mk}=\sqrt{2kE}
$$
と書ける。また、衝突中の圧力の最大値を打撃の破壊力として定義する場合、その圧力の最大値は、打撃の接触面積Sを用いて、
$$
P_{max}=\frac{v}{S}\sqrt{mk}=\frac{1}{S}\sqrt{2kE}
$$
が得られる。これが打撃の破壊力を表した式であり、打撃の威力は運動エネルギーに大きく依存する事が分かる。
ここで、バネ定数k(単位[N/m])についてもう少し説明したいと思います。そもそも、バネ定数kはバネの伸びの変化⊿Lと弾性力Fを用いて、
$$
F=k⊿L
$$
と書けます。そして、この値はバネ定数は材料の硬さを示す度合いであるヤング率E(単位[Pa])を用いて表す事が出来ます。ヤング率とは、ある材料に圧力p[Pa]を加えた時に生じるひずみ(元の長さLに対する長さの変化⊿Lの割合⊿L/Lの事)を用いて、
$$
p=E\frac{⊿L}{L}
$$
となります。材料の断面積をSとした場合、圧力pと断面積Sの積が材料に加えられた力になりますから、
$$
F=pS=ES\frac{⊿L}{L}
$$
このFに関する二式を整理する事で、
$$
k=\frac{ES}{L}
$$
が得られます。

次に、バネ定数をヤング率に置き換える事で打撃の威力を考察していきたいと思います。ヤング率Eが運動エネルギーEと文字被りして分かりにくくなるのでヤング率をE’とし、衝突する部分の断面積をS’と置き換えたバネ定数kとの関係式を代入すると、
$$
P_{max}=\frac{v}{S}\sqrt{mk}=\frac{1}{S}\sqrt{2\frac{E’S’}{L}E}
$$
この式は、衝突する部分が短くて太いほど威力が大きくなる事を示唆します。つまり、もしも同じ運動エネルギーを持っていた場合、腕が細くて長い人の突きよりも腕が太くて短い人の突きの方が威力が高い事を示しています。(これは余談ですが、15年くらい前に糸東流空手の先生からナイハンチという型で出てくる鉤突きを腹に貰ったときに余りの痛みに悶絶し、練習後に嘔吐した事がありましたが、もしかしたら、ナイハンチ突きの強さの一つは普通の突きよりも衝突部位の長さを短く出来るという利点があるのかもしれません)
次に、登場する物理量を減らす為、衝突する物体(腕など)の形状を円柱とみなして、接触面積Sと断面積Sが一致すると近似します。こうする事で、断面積S×長さLが体積Vとなり、質量mを体積Vで割った値が密度$${ρ[kg/m^3]}$$となります。これらを利用して、圧力の最大値は、
$$
P_{max}=v\sqrt{\frac{mE'}{SL}}=v\sqrt{\frac{mE'}{V}}=v\sqrt{ρE'}
$$
となり、極端な話ですが、ぶつかる部分の質量なども一切関係なくなって物体の密度とヤング率の積をルートした値と速度の積のみで破壊力が定義できるようになります。これなら軽くて高速で飛ぶ弾丸が非常に大きな破壊力を持っている事が説明できます。
勿論、人体ですから衝突する物体(腕など)の形状を円柱とみなすのは無理があります。さらには単振動のモデルでは散逸する力学的エネルギーも考慮されていません。
そこで、二章では回し蹴りなどの回転運動の衝突やエネルギー散逸についても議論する為に必要な物理学を説明して行きたいと思います。
章末問題
[問1-1]次のうち物理学的な定義や単位を持たない言葉を選びなさい「威力」「力」「エネルギー」「質量」
[解1-1]「威力」
・力は物体に加速度を生じさせる原因であり、1Nとは1㎏の物体に1$${m/s^2}$$の加速度を生じさせる力の大きさである。
・エネルギーは物体に対して仕事をする能力であり、1Jとは1Nの力を加えて物体を1m動かす仕事をする能力の事を指す。
・質量は物体が持つ運動の変化しにくさの度合いであり、その単位は㎏を用いる。
[問1-2]突きの引き手の意味を物理学的に説明しなさい。
[解1-2]「運動量保存より引き手が負の運動量を持った分だけ突き手の運動量が増える」or「作用反作用の法則により引き手を引く力の反作用によって突き手が押し出される」
・作用反作用による突き手と引き手の間での運動量のやりとりは背中を介して行われる為、背中と引き手&突き手が分離している場合には効果を持たない点に注意しましょう。また、背中の大部分を占める広背筋は打撃に必要な筋肉(ヒッティングマッスル)として知られています。

[問1-3] 武術的な意味での「質量を変化させる」を物理学的に説明しなさい。
[解1-3]
「打撃の有効質量を増やす」
これは文字通りの意味で、手打ちのパンチは手の質量だけがパンチに効いてきますが、手が腕と腕が肩と肩が肩甲骨と肩甲骨が胸郭と繋がっていけば打撃に寄与する身体の質量は増えていきます。
何年か前に山城美智先生の沖縄拳法空手が流行りましたが、「重心を揃えること」というのはすなわち有効質量を増やす事に繋がっていきます。また、「骨格を揃えること」とは打撃が当たった瞬間の身体の変形を減らす事で打撃の接触時間を減らす効果もあります(1-8参照)。
「床反力を増やす」
俗にいう重さを増やすとも呼ばれているもので、アナログ体重計に乗って膝を曲げたり伸ばしたりすると、針がさす数値が動きます。膝を曲げてしゃがむ時、体重計の針が小さくなり、曲げた膝を伸ばそうとする時に体重計の針が大きくなります。また、膝が伸びきった時、体重計の針が小さくなり元の重さを指します。
これは一見すると体重が変わっているかのように見えるのですが、実際には床反力が大きくなったり小さくなったりしているだけで、身体の持っている質量そのものや、身体が受ける重力が変わる訳ではありません。しかし、床反力を大きくする事ができると、体全体を素早く前に運ぶことができるようになります。
[問1-4] 古武術的な身体操作として「地面を蹴らない動作」や「重力によって前に出る動作」という動作があり、これを「位置エネルギーを運動エネルギーに変換している」と説明される事がある。この説明は正しいか誤っているか考察しなさい。
[解1-4] 運動エネルギーが位置エネルギーのみに由来するとは言えない。
当て身技における突き動作のバイオメカニクス的検討(参考URL:https://www.lib.fukushima-u.ac.jp/repo/repository/fukuro/R000000709/7-200.pdf)によれば、一般的な黒帯を対象とした突き動作時の重心の並進速度は約5~6m/sである。熟練者の重心の並進速度を6m/sほどと仮定した場合、その運動エネルギーは選手の質量を60kgと仮定した場合に、
$$
\frac{1}{2}mv^2=1080[J]
$$
であり、これを位置エネルギー由来とするならば、
$$
1080=mgh=60×9.8×h
$$
$$
h=1.83[m]
$$
が得られる為、すべてを位置エネルギーで賄おうとすると重心の高さを1.83[m]も下げなければならない為、不適である。実際には脚部の筋力発揮によって身体に蓄えた化学エネルギーを変換して運動エネルギーを得ている事が示される。
【コラム】MIF誤概念と武術・格闘技で用いられる物理用語
「Motion implies a force」(運動があれば力がある)
物理教育学の中にはMIF誤概念という考え方があります。これは物理学を学ぶ前の学生の大多数が持っている誤解であり、非常に強固な誤解であるため、時として多くの物理学学習者の学習を妨げています。
大学入試の問題などを解くことが得意で受験勉強としての物理では高いスコアで高校を卒業していった学生の中にもこのMIF誤概念を持っている生徒は少なくありません。実際に2018年11月に実施された共通テスト思考問題でもMIF誤概念に関する問題が出題されたのですが(出典:MIF誤概念と運動方程式 (la9.jp))、その問題の正答率はわずか3割程度でした。
この誤概念に関しては多くの物理教員や研究者たちにより研究されており、その解消のために様々な指導方法が提案されているが、万人に対して上手くいく特効薬は見つかっていません。
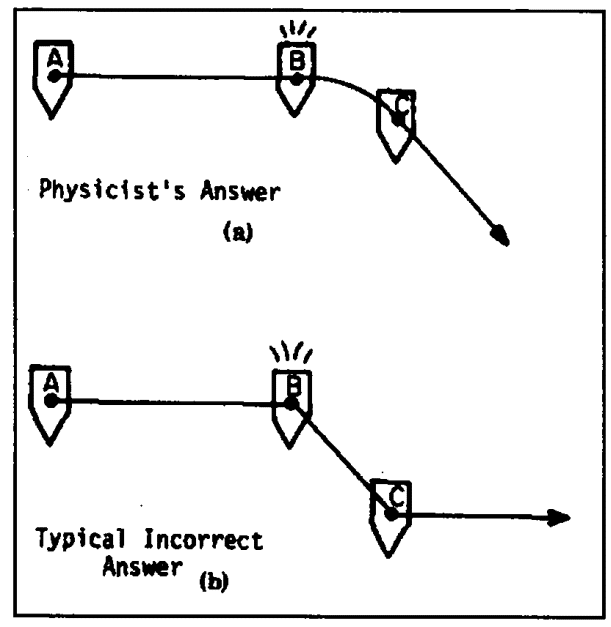
例えば、下図のように原点Oに一端を固定した糸に物体を取り付けて、矢印の方向に円運動させている運動があったとします。物体は水平で滑らかな床の上で運動するものとして、摩擦力は考慮しない(あるいは考慮しても十分に小さい)ものとしましょう。「この時、物体が受ける力を全て書いてください」と言われたらどのように書きますか?

物理学的な意味での力を見ると、円運動している物体に働く力は糸から受ける張力と重力と摩擦力しかありません。このうち、摩擦力は無視できるものとすれば、書けるのは糸から受ける張力と重力の二つになります。
円運動に対して垂直な向きに働く重力を省略して書けば、図にかける力は張力のみとなります。仮に円運動する観測者から見た力を図示する場合は見かけの力である遠心力を円の中心から外向きに書くこともありますが、それ以外の力が図に掛かれることはありません。
しかし、物理を学んでいないかあるいは物理学とは異なる定義での力を考える場合には多くの人は下図の右側のような遠心力あるいは回転力と呼ばれる力を書くと思われます。これこそがMIF(運動があれば力がある)的な力であって物理学的な力とは異なるモノになります。物理学でも回転運動の大きさを表す物理量として角運動量というものがありますが、これは力とは別物です。

あくまでも物理学でいう力Fとは物体に加速度を生じさせる(物体の運動状態を変化させる)原因であり物体間の相互作用を意味しており、力の大きさを表すN(ニュートン)という単位は1kgの物体に1$${m/s^2}$$の加速度を生じさせる力の大きさを1Nと定義しています。
加速度と言うのは単位時間あたりの速度の変化であり、速度と加速度は別物ですから、物理学で言う力の大きさとはその物体が持っている速度とは一切無関係になります。例えば、等速円運動する物体の速さは常に一定ですが、向きが変化し続ける為、速度は変化しているといえます。そして、その速度が変化する向きは中心向きであり、中心を向く加速度が存在しているといえます。そして、その中心を向いた加速度の原因となるのが、物体を糸が引っ張る張力なのです。
もし仮に回転力と呼ばれる物理学的な力があるとすれば、回転する物体は回転力を受けて接線方向に加速し続けることになりますが、そんなことは起こりません(実際に糸に付けた物体を円運動させるとき、その物体の速度が増加するようにするには中心を回転させることで糸の張力と物体の速度のベクトルをわずかに垂直ではない様にずらして糸の張力に接線方向の成分を持たせることで物体を加速させる必要があり、中心に固定された糸では物体を加速させることは出来ません)。
しかし、実際に武術的・格闘技的な説明では回転力や遠心力という言葉が好まれてよく用いられます。これらの言葉はMIF(Motion implies a force)的な力であり、物理学的な力とは定義が異なります。
MIFとは、文字通り物体の運動には力が内在するという考え方ですが、この考え方に基づいて力を定義する場合、多くの場合で力の定義は明確には決められていません。例えば、MIFに基づく力というのはエネルギーや運動量、速度や加速度といった物理学的には別の概念・物理量の総称として力という語句を使っている場合があります。これらのうちのどこまでを力と呼ぶかは人によって定義が異なり、エネルギーと力は明確に分けている人もいれば、エネルギーも力に含める人もいます。

また、MIF的な意味での力というのは、ニュートンの運動の三法則には従いません。
第一法則(慣性の法則):力を受けていない物体は静止もしくは等速直線運動し続ける。
第二法則(運動の法則):力を受けた物体には力の大きさに比例し、質量に反比例する加速度が生じる。この時、物体の質量と物体に生じた加速度の積(運動量の時間微分と等しい)が力の大きさに等しくなる。ma=F
第三法則(作用反作用の法則):力とは物体間の相互作用であり、物体Aが物体Bに力を及ぼすとき、物体Bもまた物体Aに力を及ぼし返される。その二力は大きさが等しく向きが反対である。
例えば、格闘技選手や格闘技指導者を問わず格闘技を愛するすべての人間が必ず読むべきと言っても過言ではない名著「Dr.Fの格闘技医学」の中には重力の反作用として床反力を説明している部分があるのですが、これは抜重に伴って重心が下向きの運動量を持つことを重力と表現しており、これが床にぶつかるときに大きな床反力が生じるというニュアンスで反作用という言葉を用いています。物理学的には誤用なのですが、物理学的に厳密な説明を書こうとすると分かりにくくて回りくどい表現になってしまうため、敢えて要点だけを伝えやすくするために重力の反作用は床反力であると表現したものだと思われます。
物理学的な定義に基づけば、重力の反作用は地球が人から受ける万有引力であり、人の運動には一切関係ありません。したがって、床反力と重力は作用反作用の法則には従いません。この二つの力はどちらも人間(選手)の身体が受ける力だからです。重力は常に下向きに質量×重力加速度の大きさの力が働き続けますが、床反力の大きさは可変です。例えば、膝や股関節を抜重して重心が下向きに速度を持っている状態で、それにブレーキをかけるような床反力を得る場合は重力よりも大きな床反力を得ることが出来ますし、曲げた膝を伸ばしてジャンプするときも床反力の大きさは重力よりもずっと大きくなります。
武術の世界では床反力は重力の反作用であるという説明がなされますが、これは武術的な定義の力に基づいた考え方であり、物理学とは異なる定義になります。
もし、物理法則を用いて物理学的に説明したいのであれば、物理量の定義は物理学のルールに従う必要があります。
武術を物理学で説明するとき、自分が使っている言葉が武術的な定義なのか物理学的な定義なのかを今一度確認する必要があります。定義が少しでも間違うと物理学的には全く間違っている結果が得られてしまうからです。
とはいえ、人体の運動のような複雑な現象を取り扱う場合、物理学で説明するには限界がある事ばかりなので、無理して武術家が物理学を取り繕う必要性はないと思っています。中村日出夫先生の垂木切りの様に、本当に優れた技術は物理学的な説明が出来ないものなのだと思います。

第2章 蹴りのフォームをどう評価するか?

2-1 重心と支持基底面
物体が地球から引っ張られる力を重力と呼びます。地球上に有る限りは落下中であれ水中であれ静止していようが運動していようが必ず働く力です。
人体に掛かる重力を足し合わせた時の作用点を重心と呼んでいます。
人体に掛かる重力の大きさは質量によって決まるので、短時間で変化する事は無いのですが、重心の位置は姿勢によって変化します。例えば腕を上げると重心の位置は高くなり、腰を落とせば重心の位置が低くなります。

また、地球上に有る物体は必ず重力を受ける為、それ以外に力を受けていなければ下向きに加速していきます。つまり、静止している物体には必ず上向きに重力と釣り合う力がはたらいています。スポーツ科学では床から受ける力を床反力と呼んでいます(物理学では抗力と呼んでいます)。床反力は床に垂直な成分である垂直抗力と床に平行な成分である摩擦力の合力であり、足が床を押す力の反作用でもあります。床反力は床と足の接触した部分からしか働きません。ここでは、接触点に注目してみたいと思います。

人体において床に付いた部分を結んで出来た面の事を支持基底面と呼びます。一般的に支持基底面が広いほど姿勢が安定します。例えば、片足立ちの場合はその足の裏の面積だけが支持基底面になるため不安定ですが、両脚立ちの場合は両足の面積だけではなく、両足を結んで出来た面全体が支持基底面となるので安定します。杖を付く場合は、更に支持基底面が広くなります。

人体において姿勢が安定する為には重心の位置が支持基底面の上にある必要があります。重心の位置が支持基底面の外に出た場合に人体は静止を維持する事が出来ず回転を始めてしまいます。

例えば、マイケルジャクソンのゼログラビティというダンスがあります。もしトリックが無かったとすれば、この動作ではマイケル・ジャクソンの重心が支持基底面の外に出る為に静止し続ける事が出来ずに転倒を開始する筈です。
静止した状態を維持できる事を「バランスが良い状態」とするならば、「重心の位置が相対的に低い状態」「支持基底面が広い状態」がバランスの良い状態と言えるでしょう。
また、歩行時に床から受ける床反力の変化に注目して考えてみましょう。x軸正の方向に歩行するモデルにおいて、右足が床から受ける床反力の大きさの変化を模式的に示したのが下の図になります。
鉛直方向をz方向とすると、床反力のz軸上向きの成分$${f_z}$$は人体に掛かる重力を100%とすると、接触から直ぐにピークを迎えて最大値は重力(体重)を超えてから安定し、その後は踵が地面から離れて床を蹴る動作の際に再度重力を超えるので二つの山が出来ます(二峰性)。
また、進行方向をx軸正の向きとすると、足を接地開始直後~踵・足底が接地するまでは地面からx軸負の向きの床反力を受けて、これがブレーキの役割をするが、踵が地面を離れる頃に正となり前方向への加速度の原因となります。
残るy方向に注目すると、片足が受ける床反力は若干、身体の内側方向に向いている事も分かります(※接地直後は一瞬だけ外側を向いてその後に内側を向くとするデータもある)。
この時、人体が受ける外力は重力と床反力のみですから、歩行中、片足が地面から離れている時には力がつりあう瞬間がない事が分かります。

2-2 重心と数式
重心とは質量の中心であり、その位置は重い方に偏ります。ただし、均一な材質で出来た対称な形の物体の場合は、その対称軸上に重心があるので、形によっては重心を一発で求める事が出来ます。

ただし、人体の様な複雑な物体の場合は話が別で、対称な軸上に重心があるとみなせない場合があります。しかし、この場合でも身体をパーツごとに細分化して計算する事で重心を求める事が出来ます。

したがって、重心の位置$${r_G}$$は各部位の位置$${r_1,r_2,r_3,r_4,r_5…}$$を用いて次のように書ける。
$$
r_G=\frac{m_1r_1+m_2r_2+m_3r_3+m_4r_4…}{m_1+m_2+m_3+m_4+…}
$$
2-3 重心と内力と慣性の法則
質量$${m_1}$$の骨格$${m_1}$$を質量$${m_2}$$の筋肉$${m_2}$$で質量$${m_3}$$の骨格$${m_3}$$とつないだモデルを考える。

この時、骨格$${m_1}$$は筋肉$${m_2}$$から$${F_1}$$の力で引っ張られ、骨格$${m_3}$$からは$${F_3}$$の内力を受けていたとすると、運動方程式は、
$$
m_1\frac{d^2r_1}{dt^2}=F_1+F_3
$$
筋肉$${m_2}$$が骨格$${m_1}$$から受ける反作用は$${-F_1}$$であり、骨格$${m_3}$$から受ける反作用を$${-F_2}$$とすれば、運動方程式は、
$$
m_2\frac{d^2r_2}{dt^2}=-F_1-F_2
$$
また、骨格$${m_3}$$は骨格$${m_1}$$から反作用$${-F_3}$$を受けており、筋肉$${m_2}$$から$${F_2}$$の力を受けているので、運動方程式は、
$$
m_3\frac{d^2r_3}{dt^2}=F_2-F_3
$$
と3本の運動方程式が立てられます。この3本の式を全て足し合わせると、右辺は全て消える事が分かります。
$$
m_1\frac{d^2r_1}{dt^2}+m_2\frac{d^2r_2}{dt^2}+m_3\frac{d^2r_3}{dt^2}=0
$$
此処で、両辺を$${m_1+m_2+m_3}$$で割ると、
$$
\frac{d^2}{dt^2}(\frac{m_1r_1+m_2r_2+m_3r_3}{m_1+m_2+m_3})=0
$$
となり、筋肉と骨格×2の重心位置を時間tで2階微分した値が0になる事が示されます。重心の速度は重心の位置を時間tで微分する事によって得られるので、
重心の速度は
$$
v_G=\frac{dr_G}{dt}=\frac{d}{dt}(\frac{m_1r_1+m_2r_2+m_3r_3}{m_1+m_2+m_3})
$$
$$
v_G=(\frac{m_1v_1+m_2v_2+m_3v_3}{m_1+m_2+m_3})
$$
と計算できます。これにより以下の様な関係式、
$$
\frac{dv_G}{dt}=0
$$
が得られ、この式は重心の速度は骨格同士・筋肉同士が互いに及ぼし合う内力によっては変わらない事を示しています。重心の速度を変化させる為には人体の外から力を加えなければなりません。人体のように形を変え続ける物体であっても、その重心の運動に注目すると慣性の法則(外力を受けていなければ速度の変化がゼロになる)に従う事が分かります。
補講③ 筋肉と関節。人体内で働く内力
中学理科で習う内容として関節と筋肉の関係があります。筋肉は縮む事で骨を引っ張る事が出来るので関節が曲がります。筋肉は伸びて押す事は出来ない為、曲げるのに働く筋肉があれば必ず逆に伸ばす為に働く筋肉(拮抗筋)があります。

また、筋肉と骨を繋ぐ強靭な線維性の結合組織を腱と呼んでいます。腱の中で骨と骨を直接つなぐものを靭帯と呼んでいます。腱は筋肉と異なり縮んだり緩んだりすることは出来ません。
筋肉には上図の様な紡錘状の筋肉の他に、羽状筋と呼ばれる筋肉もあります。羽状筋は筋繊維を斜めにすることで、筋束(筋繊維の束)を増やして大きな力を得ようとする筋肉であり、張力と引き換えに筋肉の収縮速度は遅くなってしまいます。
これは筋肉が1秒あたりに消費するエネルギー(仕事率)が発揮した張力(筋肉が引く力)Fと筋肉収縮の速度vの積Fvで表す事が出来る事、また、その仕事率が同じ場合には速度vを小さくする事で張力Fが大きく出来る事から羽状筋は筋収縮の速度を犠牲にしても大きな張力を得る必要がある部位(腓腹筋など)で使われています。

関節は筋肉による張力以外にも重力の影響でも曲げたり伸ばしたりする事が出来ます。また、筋肉とは関係なく関節でつながった骨が骨を引っ張ったり押したりする力(関節力)も動作には大きな影響を与えます。
例えば、手をだらんとぶら下げた状態で胸椎を回旋させて胴体を回すと、それにつられて腕も動き出します。この時、腕部の筋力は一切発揮しておらず関節によって引っ張られる力のみで動くのが分かります。
この様に身体の各部位の運動によって生じる関節力は運動依存力と呼ばれており、脱力した蹴り等には運動依存力が大きくかかわってきます。
2-4 重心とジャンプ&重心と初心者の蹴り
重心の運動に注目すると慣性の法則に従うと言う事は、重心の運動に注目すると、人体の様な形や材質が不均一な複雑な物体に対しても運動方程式を立てて考える事が出来る事を意味しています。そこで、ジャンプ動作について運動方程式を立てて考察したいと思います。
質量mの人間がジャンプする動作を
① 床と足が接触している時(外力として水平成分$${F_x}$$、鉛直成分$${F_y}$$の床反力Fと重力mgを受ける)
② 足が床から離れた時(重力mgのみを受ける)
の二つに分けて考えたいと思います。

①の運動方程式は水平方向で、
$$
m\frac{dv_x}{dt}=F_x
$$
と書けるので、水平方向の運動方程式の両辺に速度$${v_x=\frac{dx}{dt}}$$を掛けて、
$${mv_x\frac{dv_x(t)}{dt}=F_x\frac{dx}{dt}}$$
となり、これを$${\frac{d}{dt}(\frac{mv_x(t)^2}{2})=mv\frac{dv_x(t)}{dt}}$$を用いて変形すると、
$${\frac{d}{dt}(\frac{mv_x(t)^2}{2})=F_x\frac{dx}{dt}}$$
両辺をtで積分すると、
$${\int \frac{d}{dt}(\frac{mv_x(t)^2}{2})dt=\int F_x\frac{dx}{dt}dt}$$
$${[\frac{1}{2}mv_x(t)^2]^{T}_{0}=\int^{L_x}_0 F_xdx}$$
ここで、t=Tは足が床を離れるまでの時間であり、この時の速さを$${v_x}$$とする。また、重心の水平移動距離を$${L_x}$$とすると、
$${\frac{1}{2}mv_x^2=\bar{F_x}L_x}$$($${\bar{F_x}}$$は床反力の平均値)と得られるので、
$$
v_x=\sqrt{\frac{2\bar{F_x}L_x}{m}}
$$
が①が終わる時(つまり、床から足が離れる瞬間)の速度の水平成分になります。同様に鉛直方向に運動方程式を立てると、
$$
m\frac{dv_y}{dt}=F_y-mg
$$
となり、両辺に$${v_y=\frac{dv_y}{dt}}$$を掛けて時間tで積分して整理すると、
$$
v_y=\sqrt{\frac{2(\bar{F_y}-mg)L_y}{m}}
$$
が得られます。(ここで、重心の鉛直移動距離を$${L_y}$$とし、床反力の鉛直成分の平均値を$${\bar{F_y}}$$としました)
②の運動方程式は人体が外部から重力mgのみ受ける事を考えて、水平方向で
$$
m\frac{dv_x}{dt}=0
$$
となるので、速度$${v_x}$$が一定となる事が分かります。
つまり、空中での水平方向の重心速度はどんなに姿勢を変えようと、それとは関係なく一定になる事が示されます。
また、速度と位置の関係$${\frac{dx}{dt}=v_x}$$より、速度を時間tで積分して地面を離れてt秒後の水平方向への移動距離xは
$${x(t)=v_xt}$$
となります。
一方、②の運動方程式は鉛直方向で、
$$
m\frac{dv_y}{dt}=-mg
$$
となるので、速度$${v_y}$$が一定の加速度-gで減少していく事が分かり、
$${v_y(t)=v_y-gt}$$
となります。
これを時間tで積分して地面を離れてt秒後のy方向への重心位置の変化yは
$${y(t)=v_yt-\frac{1}{2}gt^2}$$
となります。
この様に、飛び上がった後の運動の様子は、飛び上がるまで(足が床についている間)にどれだけ重心に速度を与えられたかによって決まってしまいます。
すなわち、物理学的には床反力を大きく得る事と踏切開始から離陸するまでの重心の移動$${(L_x,L_y)}$$を大きくする事によって、より高く・より遠くまで跳ぶ事が出来る事が分かります。
また、空中で外部から重力以外の力を受ける事が出来なければ、重心の移動は必ず放物線を描きます。すなわち、大きな速度を持たせて跳べば高く跳べるという事であり、「滞空時間が長いけど低いジャンプ」「滞空時間が短く瞬時に最高点に上がるジャンプ」というのはファンタジーの中でしか存在しません。ジャンプ後の重心運動は飛び上がった瞬間の速度で全てが決まるのです。
また、重心と慣性の法則について、次のような例も考えてみましょう。
前蹴りを蹴る時、蹴りの初心者はへっぴり腰になりがちです。これは足を前に出した動作において重心の位置が身体の前方に移動し、尚且つ重心は元の位置にとどまろうとする性質がある為です。
また、作用反作用の法則(物体Aが物体Bに力を及ぼす時、物体Bも物体Aに力を及ぼし返し、その大きさは等しく向きは逆になる)で考えると、蹴り足を前に押し出そうとすると、腰部にはその反作用で蹴り足から押し返されるような力(内力)が働きます。すると、結果的にへっぴり腰になります。
テコンドーで理想とされる様な前蹴りでは、腰から先を軸足で押す事と上半身を後ろに下げて重心を身体に残しています。
上半身を後ろに反らす反作用で腰から先を前に押し出すという事が出来ている為、初心者と同じように重心の位置が変わらない蹴り方でもフォームが違ってきます。

補講④ 三角関数&合成関数の微分
以下の文章は、三角関数と合成関数の微分に関する文章です。必要がなければ読み飛ばして下さい。
「x-y平面上に原点Oを中心とする様な半径1の円(単位円)を書き、平面上で原点Oを中心に回転するときの半直線OPとx軸のなす角度をθ(シータ)とする。点Pは単位円上の点であり、この点のx座標とy座標をそれぞれcosθ、sinθと呼ぶ事にする」というのが、三角関数サイン(sin)とコサイン(cos)の定義ですが、言葉では分かりにくいので下図のように絵を書くと分かりやすくなります。また、cosθとsinθはθを横軸としてグラフを書くと、次の様なグラフを書く事も出来ます。
このグラフに注目すると、cosθの傾きが-sinθに対応し、sinθの傾きがcosθに対応する事が分かると思います。つまり、cosθをθで微分すると-sinθが得られ、sinθをθで微分するとcosθが得られます。

関数の中に関数が入った様な形の関数(合成関数)を微分する時には外側の関数を微分した物に内側の関数を微分した物を掛け算すれば良いという関係があります。そこで、具体的な計算を下図に示します。

2-5 二物体の単振動モデル
重心の速度が計算できる様になると、第1章で取り扱った打撃の単振動モデルについて、打撃を受けている側の質量や速度も考えた更に複雑なモデルについても取り扱えるようになります。
パンチ側の質量をm、速度をv、バネ定数を$${k_1}$$、打撃を受ける側の質量をM、速度をV、バネ定数を$${k_2}$$とし、互いに及ぼし合う力の大きさをFとします。

ここで、パンチ側をバネとみなした時の変形が$${x_1}$$、受ける側をバネとみなした時の変形が$${x_2}$$の時、
$$
F=k_1x_2=k_2x_2
$$
が成り立ちます。2本のバネの変形の合計値$${X=x_1+x_2}$$として、2本のバネを足し合わせたバネ定数をKとすると、
$$
F=KX=k_1x_2=k_2x_2
$$
とも書く事が出来、$${X=F/K}$$、$${x_1=F/k_1}$$、$${x_2=F/k_2}$$を$${X=x_1+x_2}$$に代入する事で、
$$
\frac{F}{K}=\frac{F}{k_1}+\frac{F}{k_2}
$$
となり、
$$
K=\frac{k_1k_2}{k_1+k_2}
$$
が合成バネ定数として得られます。
最初に、質量mの物体の速度がvで質量Mの物体の速度がVとすると、その運動エネルギーの総和は
$$
\frac{1}{2}mv^2+\frac{1}{2}MV^2
$$
となります。ここで、重心の速度$${V_G}$$は
$$
V_G=\frac{mv+MV}{m+M}
$$
となる事から、重心の運動エネルギーは
$$
\frac{1}{2}(m+M)(\frac{mv+MV}{m+M})^2
$$
となります。例えば、今回の様な運動の場合、外力が無い為に重心の速度は変わらず、重心の運動エネルギーは変化しません。
そこで、二物体の運動エネルギーの総和を重心の運動エネルギーとそれ以外に分けて考えたいと思います。それ以外のエネルギーをEとすると、
$$
\frac{1}{2}mv^2+\frac{1}{2}MV^2=\frac{1}{2}(m+M)(\frac{mv+MV}{m+M})^2+E
$$
となり、それ以外のエネルギーEを求めると、
$$
E=\frac{1}{2}\frac{mM}{m+M}(v-V)^2
$$
が得られます。このEを相対運動エネルギーと呼び、$${\frac{mM}{m+M}}$$を換算質量と呼びます。また、$${(v-V)}$$は二物体の相対速度であり、相対運動エネルギーとは換算質量×相対速度の2乗を2で割った値になります。
衝突後、バネの縮みが最大$${X_{max}}$$となった時に二物体の速度は重心の速度$${V_G=\frac{mv+MV}{m+M}}$$と一致する事から、力学的エネルギー保存の式を立てると、
$$
\frac{1}{2}(m+M)(\frac{mv+MV}{m+M})^2+E=\\
\frac{1}{2}KX_{max}^2+\frac{1}{2}m(\frac{mv+MV}{m+M})^2+\frac{1}{2}M(\frac{mv+MV}{m+M})^2
$$
となり、これを変形すると、
$$
E=\frac{1}{2}KX_{max}^2
$$
というスッキリとした形で書く事が出来ます。これは二物体の運動エネルギーの内、重心の運動エネルギー分は変化しない為、相対運動エネルギーと弾性エネルギーのみを考えて力学的エネルギー保存の式を立てても良い事を示しており、
$$
X_{max}=\sqrt{2E/K}
$$
となり、
$$
F_{max}=KX_{max}=\sqrt{2EK}
$$
で与えられます。これは、前章1-12で取り扱った数式と同じ形の数式になります。また、ここにEとKをそれぞれ代入する事で、互いに及ぼし合う力の最大値は
$$
F_{max}=(v-V)\sqrt{\frac{mM}{m+M}\frac{k_1k_2}{k_1+k_2}}
$$
と書く事が出来ます。この式はm、M、$${k_1}$$、$${k_2}$$を大きくする事で式全体の値が大きくなる事が示されており、$${k_2}$$とMを無限大にしてV=0とする事で1-12で取り扱った壁への衝突の式と一致します。また、m、M、$${k_1}$$、$${k_2}$$のうちのどれか1つでも0になる事で、0になる事も示されています。
例えば、ボクシングのスリッピングアウェイ(パンチが伸びる方向と同じ方向に顔を背けるようにして受け流し、パンチをかわしたり、衝撃を和らげる高等技術)はVを大きくする事で相対速度を小さくし、首を動かして攻撃を受ける部位の質量Mを小さくする事、更には相手の攻撃を正面から受け止めずに顔を背けて変形しやすくする事で$${k_2}$$を小さくする事で、相手から受けるパンチの威力を最小限にする技術であると説明する事が出来ます。
勿論、実際のパンチでは力学的エネルギー保存は成り立ちませんから、これはあくまでもいろいろな条件を限定した上での一つのモデルに過ぎません。
2-6 相対運動を考えた衝撃力の近似計算
打撃の威力について考えるときに単振動のような力学的エネルギー保存が成り立つモデルを考えるのは不自然であり、適切とは言えません。格闘技の打撃などの変形や破壊が伴う現象の場合には力学的エネルギー保存が成り立たない衝突について考える方が、適切であり、散逸した力学的エネルギーの大きさが破壊の規模を表しています。
例えば、質量Mの物体に質量mの弾丸を打ち込む現象を考える。打ち込まれる物体の速度を$${V_0}$$、弾丸の速度を$${v_0}$$とする。打ち込まれた後に、物体と弾丸が速度Vで一体となったとすると、運動量保存の法則(作用反作用の法則)より、
$$
mv_0+MV_0=(m+M)V
$$
と書けるので、一体となった時の速度Vは
$$
V=\frac{mv_0+MV_0}{m+M}
$$
となるので、重心の速度と一致する。したがって、衝突の前後で散逸したエネルギーをEとすれば、エネルギー保存の式は
$$
\frac{1}{2}mv_0^2+\frac{1}{2}MV_0^2=\frac{1}{2}(m+M)(\frac{mv_0+MV_0}{m+M})^2+E
$$
と書けます。ここで、散逸したエネルギーEは
$$
E=\frac{1}{2}\frac{mM}{m+M}(v_0-V_0)^2
$$
となり、衝突前の相対運動エネルギーと一致する。弾丸と物体がたがいに及ぼしあう力の大きさをf(作用反作用の法則より、物体が弾丸から受ける力がfならば、弾丸が物体から受ける力を-fとなる)、弾丸が物体内にめり込んだ距離をdとし、その間に物体が移動した距離をD、弾丸が移動した距離をD+dとすると、力fがした仕事(弾丸に対して-f(D+d)、物体に対してfD)を考慮して散逸したエネルギーEを表すと、
$$
E-f(D+d)+fD=0
$$
となり、これを計算することで、
$$
E=fd
$$
となり、$${E=\frac{1}{2}\frac{mM}{m+M}(v_0-V_0)^2}$$を代入して、
$$
\frac{1}{2}\frac{mM}{m+M}(v_0-V_0)^2=fd
$$
という関係式が得られます。
また、弾丸に対して運動量変化と力積の関係式は衝突時間を⊿tとして、
$$
m(\frac{mv_0+MV_0}{m+M})-mv_0=-f⊿t
$$
これを変形すると、
$$
-\frac{mM}{m+M}(v_0-V_0)=-f⊿t
$$
が得られます。これらの二式より、
$$
f=\frac{mM(v_0-V_0)}{(m+M)⊿t}
$$
$$
f=\frac{mM(v_0-V_0)^2}{2(m+M)d}
$$
が得られる。ここで、dと⊿tの間には$${d=\frac{v_0-V_0}{2}⊿t}$$という関係式が成り立っている。これらの式から、変形しにくい(dが小さい)物体程、衝突時間⊿tが小さくなり、力fが大きくなる事が示されます。
また、この計算は反発係数e=0の衝突に対応しており、反発係数がeの場合、衝突前の相対速度がVだった場合に衝突後の相対速度は-eVとなる事から、相対運動エネルギーの差は衝突前の相対運動エネルギー$${E=\frac{1}{2}\frac{mM(v_0-V_0)^2}{m+M}}$$を用いて、
$$
(1-e^2)E
$$
となり、これが散逸した力学的エネルギーであり、この大きさが打撃による破壊の規模を表しています。また、この規模はたがいに及ぼしあう力fと元に戻らない変形(塑性変形)dの積と等しくなります。
次に、打撃の衝撃力の最大値を計算したいと思います。
これまでと同様に打撃側の質量をm、ターゲット側の質量をMとして、それぞれの加速度を$${\frac{dv}{dt}}$$、$${\frac{dV}{dt}}$$と置くと、運動方程式は、
$$
m\frac{dv}{dt}=-f(t)
$$
$$
M\frac{dV}{dt}=f(t)
$$
と書けます。f(t)は互いに及ぼし合う衝撃力fの時間tに依存する関数です。
この式から、相対加速度を計算すると
$$
\frac{d(v-V)}{dt}=(-\frac{1}{m}-\frac{1}{M})f(t)
$$
これを変形すると、元々の画像でも言及している相対運動の運動方程式が得られて、
$$
\frac{mM}{m+M}\frac{d(v-V)}{dt}=-f(t)
$$
となるので、これの両辺を時間tで0→⊿tの範囲で積分すると、
$$
\frac{mM}{m+M}(v'-V'-v+V)=-\int^{⊿t}_0f(t)dt
$$
反発係数をeとすると、$${v'-V'=-e(v-V)}$$を用いて、
$$
\frac{mM}{m+M}(1+e)(v-V)=\int^{⊿t}_0f(t)dt
$$
が得られるので、これは衝突の前後で運動量の変化が力積と等しいことを示しており、右辺はたがいに及ぼしあう衝撃力f(t)の力積を意味しています。
衝撃力f(t)と時間tの関係のグラフの面積は力積$${\int^{⊿t}_0f(t)dt}$$と等しくなるので、衝撃力の最大値$${f_{max}}$$は力積$${\int^{⊿t}_0f(t)dt}$$が大きいほど大きく、衝突時の接触時間⊿tが小さければ小さいほど大きくなることが分かります。
それでは、実際の衝撃力のデータを一つ提示させてください。
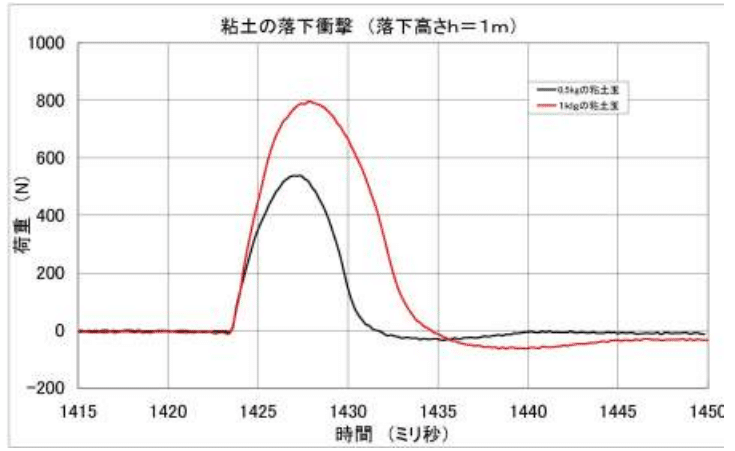
下の図は一般社団法人、日本鋳造協会のホームページに公開されている、重さ6.9kgのボーリング球を鉄板に落下させたときに得られる衝撃力の時間変化のグラフです。

接触時間⊿tは約1.3ミリ秒程度でわずかに衝突速度が速いほど⊿tが短くなっているのが分かります。
また、粘土球を衝突させた場合には衝突時間⊿tは約10ミリ秒ほどで、同じ衝突であっても材質によって衝突時間には差が大きいことが分かります。また、粘土の衝突では重い粘土の衝突程衝突時間が長くなっていることが分かります。衝突時間が長くなる為、質量を倍(赤線:1.0kg、黒線:0.5kg)にしたときに最大衝突力が倍にはなっていないことが分かります。もちろん、グラフの面積(力積)自体は倍になっています。
このような衝撃の波形を衝撃力パルスと呼び、その大きさは正矢パルスという近似式で近似できることが知られており、これを数式で書くと、
$$
f(t)≒\frac{F_{max}}{2}(1-cos\frac{2\pi t}{⊿t})
$$
となります。試しに、$${F_{max}}$$に1000[N]を代入し、⊿tに0.001[s]を代入してグラフを書くと、下の図のようになり、上の二つのグラフをよく近似できているのが分かります。

この近似を用いて、力積$${\int^{⊿t}_0f(t)dt}$$を計算すると、
$$
{\int^{⊿t}_0f(t)dt}≒\int^{⊿t}_0\frac{F_{max}}{2}(1-cos\frac{2\pi t}{⊿t})dt
$$
$$
=\frac{F_{max}}{2}[t-\frac{⊿t}{2\pi}sin\frac{2\pi t}{⊿t}t]^{⊿t}_0
$$
$$
=\frac{F_{max}⊿t}{2}
$$
これを先ほどの運動量と力積の関係式にあてはめて、
$$
\frac{mM}{m+M}(1+e)(v-V)≒\frac{F_{max}⊿t}{2}
$$
より、衝撃力の最大値は
$$
F_{max}≒\frac{2mM(1+e)(v-V)}{(m+M)⊿t}
$$
と、近似できる事が分かります。
衝撃力の最大値$${F_{max}}$$は換算質量$${\frac{mM}{m+M}}$$、相対速度v-Vに比例しており、この二つを増やせば増やすほど大きくなります。また、衝突の接触時間⊿tに反比例しており、接触時間を短くすれば短くするほど大きく出来る事が分かります。また、反発係数e(0≦e≦1)が増えれば$${F_{max}}$$も増加し、e=1の時が最大値でe=0の時の2倍になる事が分かります。
また、この式を用いた具体的な計算については3-3にて取り扱いたいと思います。
2-7 打撃のキレの物理学的定義
ここまでの衝撃力に関する物理学的な考察はあくまで二物体の衝突としてみなした場合の考え方でした。しかし、実際の蹴りでおきる衝撃は人体同士の衝突であり、二物体の衝突として近似するには厳密性に欠ける部分があります。
例えば、下のグラフは頭部への上段回し蹴りの衝撃力の時間変化を実験により測定した結果を表したものになります。このグラフを見ながら考えてみましょう。

先ず、前項で得られた数式、$${F_{max}≒\frac{2mM(1+e)(v-V)}{(m+M)⊿t}}$$を用いて、このグラフの最大値を求めてみましょう。
例えば、蹴る選手の質量を60kgとして、足の質量がその約2%なので、m=1.2kgと仮定します。頭部への打撃の場合、頭部の質量も体重の8%なので蹴られる選手の質量も60kgと仮定すれば、M=5.0kgとなりますが、下のグラフの実験で使っていたのはボブ型サンドバッグの頭部なので、ボブ型顔面ミットの質量700gからM=0.7kgとして計算してみたいと思います。蹴られる頭部は静止していたとしてV=0[m/s]、蹴りの速度をv=10[m/s]とし、衝突時間は衝撃力が観測されてからピークに達するまでの時間が3.1[ミリ秒]なので、それを2倍にして⊿t=6.2[ミリ秒]=0.0062[s]として計算すると、
$$
F_{max}≒\frac{2×1.2×0.7×(1+e)×10}{(1.2+0.7)×0.0062}=(1+e)×1.4×10^3
$$
が得られます。ボブ型サンドバッグは反発係数が低く、e=0.3程度とすると、この式が実験値と近い値を取る事が分かります。
一方、このグラフを見ると正矢パルスと近似できるのは衝撃力が計測され始めたt=5[ミリ秒]からt=10[ミリ秒]までの範囲であり、その後は緩やかに衝撃力が残っている事が分かります。
この緩やかに残っている衝撃力の正体をどのように考えれば良いでしょうか? 別の物体の衝突とみなすことは出来ないでしょうか?
そこで、二つの正矢パルスの重ね合わせによって、このグラフに似たグラフを作ってみたいと思います。

上のグラフは一つ目の正矢パルス(青)を最大値1700[N]、接触時間10[ミリ秒]として、二つ目の正矢パルス(オレンジ)を最大値300[N]、接触時間20[ミリ秒]として重ね合わせたグラフ(灰色)です。
このモデルは蹴りを一物体ではなく足部と脚部の二つの物体に分けて、二つの物体が衝突したと考えた場合のモデルになります。このように複数物体が衝突したモデルとして考えることで実際の蹴りに近似して考えることが出来そうです。
そこで、回し蹴りを足部・下腿部・上腿部の三つの物体に分けて、それぞれが衝突したものとみなしてグラフを作ってみたいと思います。

まず青線が最大値1600[N]、接触時間5[ミリ秒]とした、足部の衝突に対応する正矢パルスです。次にオレンジ線が下腿部の衝突に対応する二つ目の正矢パルスでここでは最大値200[N]、接触時間10[ミリ秒]として書いてみました。三つ目の正矢パルスは黄色で大腿部の衝突に対応するグラフで、最大値200[N]、接触時間20[ミリ秒]と仮においてグラフを作成しました。
ここで、打撃の接触時間については前項で用いた衝突の単振動モデルから質量が大きければ接触時間が長く、質量が小さければ接触時間が短い事と衝突する二物体の変形のしにくさ(弾性体であればバネ定数として表記される硬さを示した指標)が大きければ多き程接触時間が短い事が示唆されている事から、質量が大きくて関節が多くて変形の大きい部位の接触時間を長くしてグラフを作成しました。
仮説として、一般的に言われている「キレのある打撃」というのは一つ目の正矢パルスの大きさによって決まると考えられます。そのため、足部の変形がしにくく、接触時間が短くて、速度が大きい打撃が「キレのある打撃」と言えると思います。
また、「押してしまっている打撃」というのは一つ目の正矢パルスが小さく、二つ目以降の正矢パルスが大きい打撃と言えるのかもしれません。
ここからは仮説ですが、押し蹴りのような体幹部をぶつけていくような蹴りの場合には極端に書くと一つ目のピークが小さくて二峰性を描いている可能性も考えられます。

また、一般的にキレのある回し蹴りという言葉の中には引き足を取ることで接触時間を短くする事の重要性が語られることがあるのですが、別の研究結果で回し蹴りの衝撃力のデータを複数並べたもの(下図)を見ると分かるように蹴りの接触時間自体は衝撃力が大きくても小さくても大きく変わらないことが分かります。そのため、引き足によって蹴りのキレが上がるということは接触時間を短くするという事以外の要素に寄与している可能性が示唆されます。

2-8 回転運動(円運動の運動方程式)
ニュートンの運動方程式$${m\frac{dv}{dt}=F}$$に注目すると、右辺のF=0の時に速度vの時間に対する変化の割合$${\frac{dv}{dt}=0}$$となる事を示しています。これは物体に外からの力が働いていなければ、その物体の速度の変化が無い事を示しています。
この速度vは物体の位置rの時間tに対する変化の割合を意味しているのですが、運動方程式で取り扱われる速度vは重心の速度です。この様に重心が一方方向に移動していく運動を並進運動と呼びます。
形や大きさを持った物体は並進運動の他にもある回転軸周りに回転する回転運動と呼ばれる運動をしています。例えば、人体の動きについて考えてみると、人体の各部位はそこに繋がる関節を回転軸とする回転運動をしている事が分かります。例えば、走る動作などは全体の重心に注目すれば並進運動ですが関節各部位の運動は回転運動になります。
それでは、並進運動におけるニュートンの運動方程式$${m\frac{dv}{dt}=F}$$に対応する式を回転運動において考えてみたいと思います。
先ず、半径rで質量mの物体が円運動をする場合について考えます。

先ず、円運動の位置(x,y)は回転角θと三角関数を用いて(rcosθ,rsinθ)と書けます。回転角θが時間によって変化する関数である事に気をつけると、円運動の速度($${(v_x,v_y)}$$は位置を時間で微分する事で得られるので、
$$
v_x=\frac{dx}{dt}=-r\frac{dθ}{dt}sinθ
$$
$$
v_y=\frac{dy}{dt}=r\frac{dθ}{dt}cosθ
$$
従って、円運動中の物体の速度vは三平方の定理を用いて、
$$
v=\sqrt{v^2_x+v^2_y}=\sqrt{(-r\frac{dθ}{dt}sinθ)^2+(r\frac{dθ}{dt}cosθ)^2}
$$
ここで、$${sin^2θ+cos^2θ=1}$$を用いて、
$$
v=r\frac{dθ}{dt}
$$
となる事が得られます。ここで、$${\frac{dθ}{dt}}$$は角度θの時間tに対する変化の割合であり、角速度ω[1/s]と呼ばれています。
また、此処で得られた速度を用いて運動方程式$${m\frac{dv}{dt}=F}$$をxとyの2方向で立てると、
$$
x方向:m\frac{dv_x}{dt}=F_x
$$
$$
y方向:m\frac{dv_y}{dt}=F_y
$$
右辺は回転運動をする為に必要な外力の各成分($${(F_x,F_y)}$$であり、計算よりこれを求めると、
$$
F_x=-mr(\frac{dθ}{dt})^2cosθ-mr\frac{d^2θ}{dt^2}sinθ
$$
$$
F_y=-mr(\frac{dθ}{dt})^2sinθ+mr\frac{d^2θ}{dt^2}cosθ
$$
となります。各成分のうちで第一項のみを抜き出して速度と同様にこの外力Fを三平方の定理を用いて計算すると、
$$
F_o=\sqrt{\{-mr(\frac{dθ}{dt})^2cosθ\}^2+\{-mr(\frac{dθ}{dt})^2sinθ\}^2}
$$
$$
F_o=mr(\frac{dθ}{dt})^2
$$
が得られます。また、この力をxとyの2方向に分解した物が$${(-mr(\frac{dθ}{dt})^2cosθ,-mr(\frac{dθ}{dt})^2sinθ)}$$となる事から、この力は中心を向いている事が分かります
つまり、物体が円運動をする為には中心方向に引っ張られる力を受ける必要がある事を意味しています。このように円運動させる為に中心向きに働く力を向心力と呼び、向心力によって生じる加速度を向心加速度と呼んでいます。
また、力の各成分の第二項をまとめると、
$$
F_t=\sqrt{\{-mr\frac{d^2θ}{dt^2}sinθ\}^2+\{mr\frac{d^2θ}{dt^2}cosθ\}^2}
$$
$$
F_t=mr\frac{d^2θ}{dt^2}
$$
が得られます。また、この力をxとyの2方向に分解した物が$${(-mr\frac{d^2θ}{dt^2}sinθ,mr\frac{d^2θ}{dt^2}cosθ)}$$となる事から、この力は接線方向を向いていることが分かります(下図参照)

ここで、$${\frac{d^2θ}{dt^2}}$$は角速度$${ω=\frac{dθ}{dt}}$$の時間tに対する変化の割合(時間微分)を意味しており、角速度が一定の円運動(等速円運動)の場合には$${\frac{d^2θ}{dt^2}=0}$$となるので接線方向の力$${F_t}$$は0となり、中心方向にのみ力が働く円運動(半径が一定の場合)では速度が変わらないことを示しています。
力が持つ物体を回転させようとする能力を力のモーメント(トルク)と呼びます。これは回転軸からの距離と力の積(厳密に言うと位置ベクトルと力の外積)によって求められ、ある物体が回転せずに静止し続ける為には、その物体に作用する力のモーメントを回転軸周りで計算した時につりあわなければなりません。

例えば、円運動する質点が受ける力のうち、中心を向く力(向心力)$${F_o=mr(\frac{dθ}{dt})^2}$$は力のモーメントを持たず、接線方向の力$${F_t=mr\frac{d^2θ}{dt^2}}$$のみが力のモーメントを持っており、その力のモーメントは
$$
N=F_tr=mr^2\frac{d^2θ}{dt^2}
$$
と書けます。ここで、$${I=mr^2}$$と置き換えると、この式は
$$
I\frac{d^2θ}{dt^2}=N
$$
となります。これは、ニュートンの運動方程式$${m\frac{d^2r}{dt^2}=F}$$と非常によく似た式の形をしていることから、回転の運動方程式と呼ばれ、ニュートンの運動方程式における質量mが物体が持つ速度変化のさせにくさを表しているように、Iは物体が持つ角速度変化のさせにくさの度合いを表しており、このような回転しにくさを表すIを慣性モーメントと呼んでいます。
半径rと質量mが大きいほど慣性モーメント$${I=mr^2}$$が大きくなることから、物体の回転しにくさが増すことが分かります。
運動量を質量mと速度$${v(=\frac{dr}{dt})}$$の積であるmvと定義したように、角運動量を慣性モーメントIと角速度$${ω(=\frac{dθ}{dt})}$$の積であるIωと定義します。(運動量と角運動量は別の物理量である点に注意)
また、運動エネルギーが$${\frac{1}{2}mv^2}$$と定義されるように回転する物体が持つ運動エネルギー(回転エネルギー)は$${\frac{1}{2}Iω^2}$$と表すことができます(角運動量と運動量は別物ですが、この2つのエネルギーは同じエネルギーの表記の違いである点に注意してください)。
これは、慣性モーメント$${I}$$が$${I=mr^2}$$である事と、等速円運動の速さは半径と角速度の積で求められ、$${v=rω}$$となる事から導けます。
$$
E=\frac{1}{2}mv^2=\frac{1}{2}m(rω)^2=\frac{1}{2}mr^2ω^2=\frac{1}{2}Iω^2
$$
また、外力を受けない場合に運動量が保存されるように、外力を受けないか受けてもその力が回転中心を向いていて力のモーメントがゼロの場合には角運動量も保存されます。
2-9 実際の回転運動(角運動量保存)
実際の円運動について考えるため、先ずは真上にジャンプしながら水平回転する時について考えます。
空中では身体に働く外力は重力だけなので、重心の並進運動は重力の影響だけを受けます。真上に奇麗に飛び上がった場合は、ジャンプ開始時が上向きに最大の速度を持っており、上向きの速度が減速していき速度が0となった後に下向きに加速して初速度と反対に等しい大きさの速度を持って着地します(鉛直投げ上げ)。
すなわち、縦回転にしろ横回転にしろ如何なる回転運動であっても、それが空中で回転する場合、回転軸は必ず重心を通ります。
宇宙には連星や双子星と呼ばれる二つの恒星が互いを万有引力で引っ張りあって円運動する天体が存在するのですが、この天体も二つの恒星の重心を中心と取るように互いに円運動をしています。

また、外力が重力(重心を通る回転軸周りの力のモーメントはゼロになる)しかない為、回転ジャンプ中で角運動量保存$${Iω=mr^2ω}$$は保存します。例えば、ジャンプ中に手を広げるなど半径rが増えた場合には人体の慣性モーメントが増えるため、角速度ωが減少することが分かります。
したがって、ターン蹴りや540度を上手く蹴れるようになる為には、地面に足がついているうちに慣性モーメントの大きい状態(手を開いた状態)で角運動量を大きく作ることが肝心であることが分かります。そして、飛び上がった後に腕を閉じて慣性モーメントを小さくすることで、回転の角速度を上げることが540度などのトリッキングの蹴りのコツになります。
また、角運動量保存の観点から考えると、回転蹴りの得意不得意に男女差がある理由も説明できます。確かに、ルース・バグビーの様に回転蹴りが得意な女子選手も居ますが、回転蹴りが苦手な女子選手も少なくありません。筋力などの差もありますが、物理学的に考えた場合は一般的な体系の男子選手と比較して骨盤が横に広く(下半身の慣性モーメント$${I}$$が大きく)、肩幅が狭くて上半身が細い(上半身の慣性モーメント$${I}$$が小さい)事が回転蹴りにとってはネックになります。
角運動量は$${Iω}$$となるので、同じ角運動量でも角速度$${ω}$$を2倍にすると、慣性モーメント$${I}$$は1/2倍になるのですが、回転する物体が持つ運動エネルギー(回転エネルギー)は$${\frac{1}{2}Iω^2}$$なので、角速度を2倍、慣性モーメントを1/2倍にした場合に回転エネルギーは2倍になってしまいます。つまり、同じ角運動量を作るにしても慣性モーメントが大きければ大きいほど必要なエネルギーが小さい事が分かります。
つまり、回転蹴りを上半身で角運動量を作って下半身に角運動量を移動させたい場合、上半身に慣性モーメントが大きい男子選手の方が少ないエネルギーで上半身に角運動量を作る事が出来、骨盤の慣性モーメントが小さい男子選手の方が同じ角運動量でも骨盤に大きな角速度を得る事が出来るので、結果的に速い蹴りを蹴る事が出来るのです。
2-10 慣性力と遠心力
日常用語と物理用語の乖離が著しい単語として「遠心力」という物があります。例えば、後ろ回し蹴りなどに対しても「WTテコンドーの蹴り方は遠心力で蹴っている」という風に使われています。2-7で円運動について説明した時に一切「遠心力」という語句を用いなかった様に、遠心力という力は存在しません。では、物理用語としての遠心力とは一体、どのような言葉なのでしょうか?
物理学では「見る人」(物理学的には観測者と呼ぶ)によって同じ現象を説明する場合でも、立てる方程式が異なる事があります。例えば、身体全体を加速させて前に進む様な回し蹴りを蹴る際に、特に意識をしなかったり、体幹が弱ければ上半身は慣性(その場に止まろうとする性質)によって自然と後ろにのけぞってしまいます(下図、左)。
これは外から見れば、特に上半身に対して後ろ向きに力が働いている訳ではありません。むしろその逆で、上半身に対して前向きに力が働いていないから加速度を生じさせることが出来ずにその場に残る様にして後ろに下がってしまうのです。
しかし、これを蹴る人自身(下図、右)から見ると、上半身を後ろに引っ張る様な力を受けている様に感じます。この様な加速度を持った人にとってのみ観測される見かけ上の力を慣性力と呼んでおり、遠心力は慣性力の一種です。

ただ、外部からは観測されない見かけ上の力と言っても、「実態のない力」という意味では決してなく、非慣性系(加速度運動する観測者)においては運動方程式に従って物体の運動量を変化させるれっきとした力であり、特にスポーツにおいては慣性力を考える事は非常に有意義になります。
例えば、肩関節から先の腕の動きだけに注目して考える時には肩関節に固定した観測者は肩関節の加速度に応じた慣性力が腕に働いている様に見えますから、人体の各部位に注目して動作を解析する時には慣性力を無視できない場合も往々にして存在します。つまり、慣性力の一種である遠心力も、動作全体を外から見て考える時には存在しない力ですが、身体の内側に観測者を置いて考える時には実態(物体の運動量を変化させ、形を変形させる)を持った力になります。
加速度運動する観測者から見た慣性力は観測者の加速度をa、物体の質量をmとすると、
$$
f=-ma
$$
と書く事が出来ます。この式のマイナスは慣性力の向きが観測者の加速度と逆向きになる事を意味しています。また、慣性力の作用点は慣性力を受ける部位の重心になります。
下図のように関節Oに質量mの骨格Aが繋がっているモデルを考えます。ここで、関節Oを右向きに加速度aで加速させた場合の骨格Aの運動について考えてみましょう。

ここで、この運動を外部から見た場合(下図、左)には骨格Aを関節Oが引く力fの向きや大きさは常に変化する事から、骨格Aの重心の軌道は複雑で、骨格Aに対する運動方程式を
$$
m\frac{dv}{dt}=f
$$
としても、これを解いて軌道を解析するのは困難です。
しかし、関節Oに固定した観測者が内側から運動を見た場合には骨格Aは慣性力maを受けて、その力のモーメントによって円運動するシンプルな運動として取り扱う事が出来ます。この様に、人間の身体の様な複雑な物を対象とした場合には観測者を変えて考える事が有効であり、その際には慣性力は決して無視できない力になります。
よく「遠心力で蹴る」蹴りの代表例として挙げられるのがWTテコンドーの後ろ回し蹴り(ティフリギ)でしょう。
※ ITFテコンドーの後ろ回し蹴りとは蹴り方が大きく異なるので、此処ではWTテコンドー式のティフリギに注目した話となります。
WTテコンドーで後ろ回し蹴りと呼ばれる蹴りの韓国語には「ティフリギ」の他にマイナーな呼び方で「モンドルリョチャギ」というものがあります。これを直訳すると「胴体を回す蹴り」という意味です。道場や選手によって蹴り方は様々ですが、多くのWTテコンドー道場で指導される後ろ回し蹴りの基本的な蹴り方は、最初に胴体を回転させてから蹴り足を出しています。

物理学的な説明をするならば「最初に上半身を回転させて角運動量を作り、途中から上半身の回転を止め(もしくは逆回転させ)て、上半身で作った角運動量を蹴り足に移す事で蹴り足を加速させる」というのがWTテコンドーのベーシックな後ろ回し蹴りの蹴り方になります。
では、「遠心力で蹴る」とはどういった意味を持つのでしょうか?
先ず、遠心力とは慣性力の一種であり、円運動する観測者からしか見えません。円運動する物体は中心向きに向心加速度という加速度を持っており、この向心加速度に由来する慣性力が遠心力なのです。
例えば、下図のように糸で引っ張って張力Sを受けている円運動を考えたいと思います。その場合、向心加速度aを用いて運動方程式はma=Sと書けます。一方、円運動する観測者から見た場合、静止して見えるので、運動方程式は成り立たず力のつりあいが成り立つ事になります。ここで、ma=Sと全く同じ式が立てられるのですが、このmaは遠心力を意味します。

遠心力とは円運動の中心から外側に向かって働く力ですが、外からは決して観測される事はなく円運動する内側からしか見えない見かけの力となります。また、遠心力の大きさは速度v、角速度ω、半径rを用いると、
$$
ma=m\frac{v^2}{r}=mrω^2
$$
WTテコンドーの後ろ回し蹴り(ティフリギ)の場合、最初に胴体を大きく回転させる事から、蹴っている選手自身からは遠心力を受けて足は自動的に円の中心から外側に向かって伸びていく様な蹴りになるので、これを「遠心力で蹴る」と呼んでいるのではないでしょうか?
2-11 脛と足の甲、どちらで当てるか?
さて、回し蹴りを相手に当てる時、蹴り足の先端部分と膝に近い部分のどちらで当てた方が威力が出るでしょうか? 足の甲で蹴る事が多い我々WTテコンドー勢にとっては馴染みの薄いことかもしれませんが、物理学的な見地から考えてみたいと思います。
先ず、回転運動を見た時に円運動の速さvと角速度(1秒あたりの角度の変化)ωの間には、
$$
v=rω
$$
という関係が成り立っています。したがって、同じ角速度であれば半径が大きいほど速さが増します。つまり、外側に行けば行くほど運動量が大きくなり、威力が増すというのは経験則的に言える事かもしれません。
ただ、果たして本当にそうなのでしょうか?
先ず、下図のように蹴りを質量m長さrの棒と見立てます。また、回転軸は固定し動かないものとします。そして、ターゲットの回転軸からの位置を$${l}$$とし、角速度ωで回転しているとし、ターゲットは質量が十分に大きい為、ターゲットとの衝突で棒(蹴り足)は停止した物とします。この時、棒(蹴り足の)慣性モーメントIは、
$$
I=\frac{1}{3}mr^2
$$
と書けます。この慣性モーメントIを用いてターゲットに当たっている瞬間の回転の運動方程式は、
$$
I\frac{dω}{dt}=l×\bar{F}
$$
と書けます。ここで、$${\bar{F}}$$はターゲットから受ける反作用(=蹴り足がターゲットに及ぼす力。作用反作用の法則に基づく)の平均値とします。また、接触時間は⊿tとし衝突は短時間で行われる為に小さな値となります(1-3で取り扱った内容と同様に平均値$${\bar{F}}$$の大きな蹴りが最大値の大きい蹴りであり、破壊力の大きい蹴りとみなせる)。
$$
\bar{F}=\frac{mr^2ω}{3l⊿t}
$$

此処で得られる解はターゲットまでの距離$${l}$$が分母に来ている事から(ターゲットの質量が十分に大きい&回転軸が固定されている場合には)回転軸に近い場所(脛など)を当てて蹴った方が威力があるという事を示しています。
例えば、フルコン空手のローキックの一種で脛を落とすローキックと呼ばれる蹴りは膝に近い脛の上部を相手にぶつけています(参考動画:https://www.youtube.com/watch?v=JAALXw3irtI)。テコンドーの組手でも、ターン蹴りの時に相手との距離が詰まってしまい膝が当たってしまうと大きなダメージを与えてしまったりします。
とはいえ、WTテコンドーでは相手の回し蹴りを受ける際に距離を潰してディフェンスをする訳で、軸に近い詰まった距離で当たった時の方が威力があるというのは経験に反する感じがします。
そこで、1-3で示した蹴りの速度と時間のグラフを再掲しますのでこれに注目してみてください。

これは回し蹴りが蹴り始めた瞬間から大きな速度を持っている訳では無く、時間と共に加速していく様子を示しています。(足首の速さの最大値はt=1.9付近で14.6[m/s]※時速52.5kmとなる。)
つまり、WTテコンドーで相手の回し蹴りに対して距離を潰してディフェンスをする事があるのは、蹴りの速さが小さいうち(グラフで言えばt=1.6~1.7の間)に相手の蹴りを潰してしまおうという考え方がある為です。
では、この回し蹴りの回転運動に注目して考えたいと思います。膝から見た足首の相対速度(膝関節を回転軸として固定した座標系における足首の速度)は回転運動(の先端)の速度を表しており、グラフは下の様になります。回転運動の最高速度は11.6m/s(=42.6km/h)となっています。また、角速度を計算すると、この選手の下腿の長さ0.411mを用いて角速度の最大値ω=28.6[rad/s]が得られます。
此処で、下腿の回転運動のエネルギーを計算したいと思います。下腿全体の質量をmとした場合、慣性モーメントは$${I=\frac{m×0.411^2}{3}}$$であり、回転運動のエネルギーは$${E=\frac{1}{2}Iω^2}$$となる事から、下腿の質量を選手の質量63kgの6%と仮定すると、m=3.8として、
$$
E=\frac{1}{2}\frac{3.8×0.411^2}{3}28.6^2=87.5[J]
$$
が得られます。

また、膝の速度に注目した下のグラフをみるとインパクトの瞬間(t=1.9近辺)になると膝の速度が減速していき、運動量が脛に移っていく様子が分かります。
仮に脚全体(下腿・膝・上腿)が同一の回転運動とみなせる円運動をしていた場合、中間地点となる膝部の速度は足首の速度の半分程度(5~6m/s)となるはずですが、足首が最高速度になるt=1.9付近では膝の速度は2~3m/sまで減速しています。下腿の角速度が最大になったt=1.896sでのデータを見ると、膝の速度は2.097m/sであり、これを下腿の並進運動の速度と考えると、運動エネルギー$${E=\frac{1}{2}mv^2}$$は、先ほどのmと同様の値を用いて、
$$
E=\frac{1}{2}×3.8×2.097^2=8.36[J]
$$
となり、エネルギーベースで見た時に下腿部の並進運動の持っているエネルギーは回転運動が持っているエネルギーの約9.6%ほどの大きさしか持たない事が分かります。つまり「並進運動が大きいのでWTテコンドーの回し蹴りは先端で蹴った方が威力が出る」という擁護も難しい事が分かります。

以上の事より、WTテコンドーの中段回し蹴りは辛い言い方をすれば、射程距離は長くなるのですが、その分だけ破壊力という点において脛で蹴る蹴り方に劣るというのが物理学的な見解になります。したがって、相手に効かせる蹴りという観点で見た場合には足の甲で蹴るという蹴り方では相手に打撲的なダメージを与える蹴りを狙うよりも、鳩尾や肝臓などの急所をピンポイントで狙う蹴り方が必要になります。
とはいえ、仮に腰部速度を重心速度と近似した場合、腰部の速度は蹴りが当たり始めたt=1.896[s]で1.97[m/s]、蹴り足の速度が0となるt=1.932[s]で1.31[m/s]。この重心の速度分の並進運動のエネルギーを蹴り足の下腿以外の部分が持っているエネルギーと仮定すると、運動エネルギーの減少分は
$$
\frac{1}{2}×(63-3.8)×(1.932^2-1.31^2)=59.7[J]
$$
であり、下腿の回転運動のエネルギー87.5[J]+下腿の並進運動のエネルギー8.36[J]=95.86[J]の60%に上る事から、全身の並進運動のエネルギーを増やす事が出来れば、WTテコンドー流の回し蹴りであっても威力向上に繋がる事も示唆されます。

2-12 固定されてないターゲットを蹴る場合
先程はターゲットの質量を無限大(動かないもの)としていましたが、今度はターゲットの質量をMとして自由に動く場合について考えてみます。例えば、頭部などを蹴る場合には相手の質量を壁とみなす事は出来ないでしょう。
下のグラフはティフリギをハンドミットに打ち込んだ際の足首の速度の様子ですが、ハンドミットを振り抜いた蹴りの為、ビッグミットへの回し蹴りの様に蹴り足が急激に減速する様子は見られません。質量が無限大の場合との違いが良く分かります。

さて、ここで蹴りをモデル化して計算に移りたいと思うのですが、未知数が多すぎると計算で出た値の評価が難しくなる為、スーパースローの動画(参考動画:https://www.youtube.com/watch?v=6E-JTXpyGAg)で打撃が頭部に当たる瞬間を観察して未知数を減らしたいと思います。すると、衝突直後は打撃部と頭部の速度がほぼほぼ一致していた為、衝突は完全非弾性衝突(衝突直後のターゲットと衝突物体の速度が一致し、エネルギー散逸が最大になる衝突)とみなせるとします。
衝突直後のターゲットの速度をVとすると、回転軸周りの角運動量保存の式を立てると、下腿の質量を先ほど同様にm、長さをr、当たる位置の距離をlとして角運動量がωからω’に変化したとして、
$$
\frac{1}{3}ωmr^2=\frac{1}{3}ω’mr^2+MVl
$$
また、完全非弾性衝突なので、衝突直後のターゲットの速度Vは衝突直後の衝突部位の速度lω’と等しくなる事から、
$$
V=\frac{3ωmr^2l}{3mr^2+9Ml^2}
$$
となり、ターゲットが及ぼされる力積F⊿tは運動量の増加量MVと等しい事から、
$$
F⊿t=\frac{3ωmMr^2l}{3mr^2+9Ml^2}
$$
が得られます。

例えば、角速度ωは分子のみに有るので角速度を増やせばそのまま蹴りによる力積F⊿tが大きくなり、ターゲットに及ぼす力(あるいは圧力)も増える事が分かりますが、それ以外については式が複雑であり考察が難しくなります。ここで、選手の質量を男子63kg級として具体的な数値を代入して考えてみたいと思います。頭部の質量は約10%なのでM=6.3[kg]、先ほどと同じ条件でm=3.8kg、r=0.411m、ω=28.6[rad/s]を代入してみます。
すると、及ぼす力積と当たった位置の回転軸からの距離l(横軸)の関係は次のようになります。

足の長さのほぼ半分の位置(l=0.19[m])の時に力積が最大になる事から、上段回し蹴りにおいても一番効かせられるのは脛の中心である事が示されます。
ただ、先端部分のl=0.41mで当たった場合でも最大値の76%ほどの力積を出せる事から条件によっては十分に倒せる蹴りになると思われます。
さて、今度は先ほどの「(ターゲットの質量が十分に大きい&回転軸が固定されている場合には)回転軸に近い場所(脛など)を当てて蹴った方が威力があるという事を示しています。」について検証する為、下段や中段などの攻撃におけるターゲット部位の質量Mに63kg(相手の全体重)を代入してグラフを作ってみたいと思います。このグラフは膝からの距離が7cmの時に最大値を取っています。したがって、下段蹴りや中段蹴りでは脛の上部を相手に当てる様に蹴る蹴り方が有用である事を示しています。ただし、詰まり過ぎた蹴りに関しては威力が低いと言う事も同時に示しています。

また、ターゲットの質量を徐々に変えながら力積を最大とする回転軸からの距離lを計算した物をグラフにすると次のように書けます。(条件は先ほど同様蹴り足の質量m=3.8kgで蹴り足の下腿の長さr=0.411m、角速度ω=28.6[rad/s])ターゲットの質量が蹴り足の質量と比べて十分に小さい場合には足の先端近くを当てる事で大きく力積を得る事が出来る事が分かります。例えば、ハンドミットの様な軽いターゲットを蹴る場合には先端部分を当てる事が有効であり、ハンドミットを脛で蹴っても力を上手く伝える事は出来ません。脛で蹴る蹴りを身に付けるためにはキックミットやビッグミットなど質量の大きな(この手のミットの場合におけるターゲット質量はミットの持ち手分も加算される)ミットを蹴る必要があります。

2-12 撃心(スイートスポット)とは?
バットやラケットなど形がある物体が球体と衝突するとき、バットやラケットには衝突の前後で速度が変わらない点が現れる事があります。この点は速度が変わらないことから加速度がゼロとなり衝撃もゼロになります。
すなわち、バットなどの物体が衝突したときに、衝撃がゼロになる点とグリップ部分が一致すれば身体に掛かる負担が少なくなります。
このような、グリップ部分への衝撃を最も少なくする衝撃点を(グリップ部分に対する)衝撃の中心(撃心)と呼びます。
下図のような静止した棒に対してボールが衝突する場合について考えてみましょう。

衝突で、衝突により棒(質量m)とボールでやり取りする力積をF⊿tとすると、重心速度$${v_{CG}}$$は、運動量変化と力積の関係より
$$
mv_{CG}=F⊿t
$$
とかけるので、$${v_{CG}=\frac{F⊿t}{m}}$$が得られます。
また、重心まわりの棒の慣性モーメントをIとして、角運動量の変化は力積のモーメントと等しくなるので、
$$
Iω=aF⊿t
$$
とかけるので、$${ω=\frac{aF⊿t}{I}}$$が得られます。ここで、P点の速度$${v_P}$$は左向きを正とすると、回転速度と並進速度を合わせた速度として得られるので、P点の重心周りの回転運動による速度がbωである事から、
$$
v_P=\frac{F⊿t}{m}-ωb
$$
$${v_P=0}$$となるようなaがP点に対する撃心になります。
したがって、撃心の重心からの距離aは(バットの重心周りの)慣性モーメントI、重心からグリップまでの距離b、バットやラケットなどの質量mを用いて
$$
a=\frac{I}{bm}
$$
と書けます。撃心は衝撃の中心とも呼ばれており、野球ではスイートスポットと呼ばれる点が撃心に当たる点になります。
例えば、長さLで質量mの棒の重心まわりの慣性モーメントは、重心を棒の中心とすると、慣性モーメント$${I=mr^2}$$より、長さrの棒の重心まわりの慣性モーメントは、
$${I=\int^{1/2}_{-1/2}\frac{m}{r}x^2dx}$$
$$
I=\frac{1}{12}mr^2
$$
となるので、2-11で用いたモデルにおいて回転軸に対する撃心の重心からの距離aは、
$$
a=\frac{1}{12(r/2)m}mr^2=\frac{1}{6}r
$$
となるので、重心を脛の中心と近似した場合に膝から$${(\frac{1}{2}r+\frac{1}{6}r=)\frac{2}{3}r}$$だけ先、つまり脛を2:1した点(くるぶしよりも数センチ上のところ)で当てると膝への負担は一番小さくなるようです。
2-13 最速降下問題
あるx-y平面上で、原点Oから点P(2a,2b)まで向かう物体の最短経路が直線と言うのは疑いようがありません。しかし、原点Oから点Pに到達するまでの時間を最短にする場合、その経路が直線とは限りません。
例えば、OからPまで速度が一定の場合には原点Oから点Pを結んだ直線が最短経路になり時間も最小となるのですが、y<aを満たす範囲を領域A、a<yを満たす範囲を領域Bとして、領域Aを通過する時の速さが$${v_A}$$、領域Bを通過する時の速さを$${v_B}$$であったとすると、状況が変わってきます。
例えば、$${v_A>v_B}$$だったとするならば、領域A中を通過する距離を長く取り、領域B中を通過する距離を短くする事で、OPを一直線に進むよりも時間が短縮されます。この時、領域Aと領域Bの境いとなる通過点をQ(b+d,a)としてO→Q→Pとなるまでの時間tの距離dに対する関数t(d)を計算してみましょう。
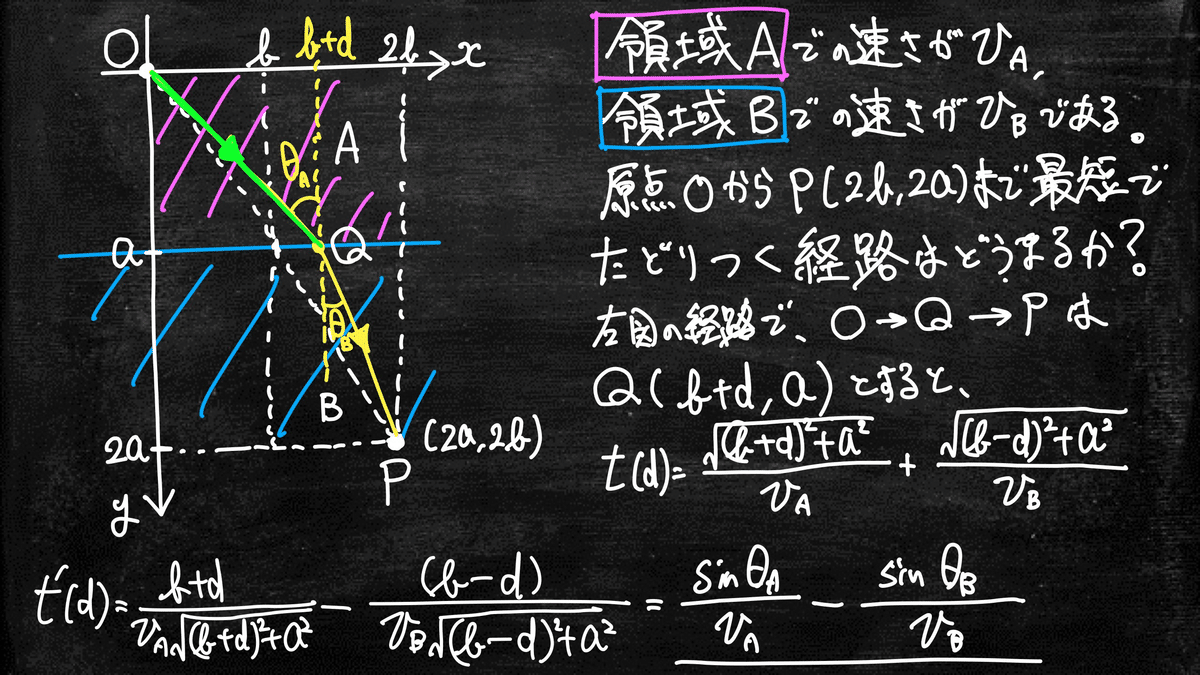
先ず、$${OQ=\sqrt{(b+d)^2+a^2}}$$であり、$${QP=\sqrt{(b-d)^2+a^2}}$$となるので、
$$
t(d)=\frac{\sqrt{(b+d)^2+a^2}}{v_A}+\frac{\sqrt{(b-d)^2+a^2}}{v_B}
$$
が得られます。
ためしに、縦軸に時間tを取り、横軸に距離dを取ってa=b=10,$${v_a=11,v_b=9}$$と適当な数値を設定してみた上でグラフを書くと下の図の様なグラフが得られます。
このグラフは、d=1.94近辺で最小値を取る事から、dの値をある一定まで増やしていくと経過時間は小さくなるが、その後は経過時間が長くなっていく事が示されます。この最小値の時に接線の傾きが0になる事から、時間t(d)をdで微分した値が0になる時が最小値の条件と言えます。

そこで、t(d)をdで微分すると、
$$
t'(d)=\frac{b+d}{v_A\sqrt{(b+d)^2+a^2}}-\frac{b-d}{v_B\sqrt{(b-d)^2+a^2}}
$$
が得られ、図のように入射角を$${θ_A}$$、屈折角を$${θ_B}$$と置く事で、
$$
t'(d)=\frac{sinθ_A}{v_A}-\frac{sinθ_B}{v_B}
$$
が得られるので、この値が0になる時(つまりt(d)が最小値となる)は
$$
\frac{sinθ_A}{v_A}=\frac{sinθ_B}{v_B}
$$
を満たす時である事が分かります。このような、速度の異なる二つの領域を進むときに最小時間で進むための入射角と屈折角の条件をスネルの公式と呼び、例えば空気中から水に入射する事で屈折する光の入射角と屈折角などはこのスネルの公式にしたがっている事が知られています。
では、今度は鉛直下向きにy軸を取ったx-y平面上で原点Oから点P(a,b)まで球を転がした場合、OからPまで達するまでの最小時間を求めたい。力学的エネルギー保存の法則に従うので、y座標がyの時の速さを$${v}$$とすると、原点を重力による位置エネルギーの基準点として、
$$
0=\frac{1}{2}mv^2-mgy
$$
$$
v=\sqrt{2gy}
$$
が得られる。ここで、y軸上でy=bまでをn等分して、そのn等分されたそれぞれの速さが、y座標$${y_i}$$に対して
$$
v_i=\sqrt{2gy_i}
$$
と与えられる。

区間iにおけるx方向の移動距離を$${⊿x_i}$$、y方向への移動距離を$${⊿y_i}$$とすると、
$$
sinθ_i=\frac{⊿x_i}{\sqrt{(⊿x_i)^2+(⊿y_i)^2}}
$$
が成り立ち、i→i+1の間でスネルの公式は、
$$
\frac{sinθ_i}{v_i}=\frac{sinθ_{i+1}}{v_{i+1}}
$$
が成り立つ。これが、各区間に対して成立し続けるので、
$$
\frac{sinθ_1}{v_1}=\frac{sinθ_2}{v_2}=…=\frac{sinθ_n}{v_n}
$$
となり、これが一定の値を取る事から、
$$
\frac{sinθ_i}{v_i}=\frac{⊿x_i}{\sqrt{2gy_i}\sqrt{(⊿x_i)^2+(⊿y_i)^2}}
$$
$$
={2gy_i[1+(\frac{⊿x_i}{⊿y_i})^2]}^{-\frac{1}{2}}
$$
となり、ここでn→∞として区間を無限に細かく設定する事で、
$$
y[1+(\frac{dy}{dx})^2]=2C
$$
という方程式が与えられます。2Cは一旦仮置きしただけの定数であり、様々な条件によって与えられる事となります。
そして、この方程式の解が点O→点Pにおいて経過時間tを最小とする曲線になります。この方程式の解は
$$
x(θ)=C(θ-sinθ) , y(θ)=C(1-cosθ)
$$
と与えられる事が知られています。試しに、元の方程式に代入してみたいと思います。
先ず、$${\frac{dx}{dθ}=C(1-cosθ)}$$かつ$${\frac{dy}{dθ}=Csinθ}$$より、$${\frac{dy}{dx}=\frac{sinθ}{1-cosθ}}$$が得られ、これを元々の方程式の左辺に代入する事で、
$$
C(1-cosθ)(1+(\frac{sinθ}{1-cosθ})^2)=2C
$$
が得られるので、元々の方程式$${y[1+(\frac{dy}{dx})^2]=2C}$$を満たしている事が分かります。
ここで得られる曲線をサイクロイドと呼びます。
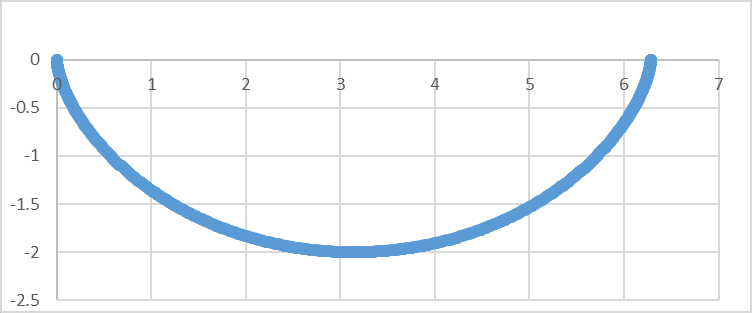
武術には流派によっては重心がサイクロイドを描く事で最速の突きが出せるという説明がなされる事があります。
これを実現させた場合、重心の動きをサイクロイドに一致させた動作の場合、原点から最下点までだけを見ても進行方向へ3進む間に鉛直方向に2沈む必要があります※。
試しに下の図はWTテコンドーの歩き立ち→前屈立ち中段突き動作の最初と最後の重心位置をサイクロイドに重ねた場合の絵ですが、このような重心の動きを実現する為には一度大きく沈み込む必要がある為、WTテコンドーのチルギ動作にはサイクロイド云々は当てはまらない事が分かります。

一方、トルリョチャギの蹴り始め動作だけを抜き出した場合、選手によっては重心の軌道がサイクロイドによく似た曲線を描いている場合もあります。これについては個人差があり、主に90年代の古い時代の選手が使う速くて長い蹴り方の中にサイクロイド曲線の様な軌道がよく見られます。
また、蹴りの動作を観察していると頭部の軌跡にサイクロイドに似た曲線が見られる場合もあります。
蹴りの動作自体は重力のみならず床反力の影響が大きく、筋力発揮によって姿勢を制御している為、一概に局面を転がすボールと同じ様に考える事は出来ないのですが、局所局所に注目すると、サイクロイドに似た軌跡を描く事があり、これらの動作が効率の良い蹴りに一定の寄与をしているのかもしれません。

補講⑤ オイラーラグランジュ方程式
こちらも読み飛ばしていただいて問題ありません。
原点Oとx軸上のある点A(a,0)を繋いだ線を書こうとすると無限に存在します。そのうち、最短経路を通る線はy=0をみたす直線であることは自明ですが、これを証明するにはどうすればよいでしょうか?
まず二点OAをつなぐ関数y(x)の長さを求めたいと思います。この関数はどのような関数でも良いので曲線であり、三平方の定理では長さLが求まりません。しかし、直線とみなせる範囲まで拡大した微小な長さdLであれば、三平方の定理で計算できます。この時、グラフのx方向への変位dxとy方向への変位dyを用いて、三平方の定理から、
$${dL=\sqrt{(dx)^2+(dy)^2}=dx\sqrt{1+(\frac{dy}{dx})^2}}$$
と書けます。これをx=0→x=aについて積分することで、2点OAをつなぐ任意の関数y(x)のグラフの長さL[y(x)]を求めることが出来、
$${L[y(x)]=\int^a_0\sqrt{1+(\frac{dy}{dx})^2}dx}$$
と書ける関数の中に関数が入った関数を汎関数と呼びます。
関数y(x)の極値を求めるとき、関数を微分した値が0になる時が極値となり、
$${y´=\frac{dy}{dx}=0}$$ つまり、 $${dx=0}$$
を満たすようなときが極値の条件であることと同様にして、関数yの微小な変化δyに対応した汎関数の変化δL=0となる時、汎関数もまた極値と呼べます。※δもデルタと読みます。
$${δL[y(x)]=\int^a_0\sqrt{1+(y´+δy´)^2}dx-\int^a_0\sqrt{1+(y´)^2}dx}$$
ここで、δyは非常に小さな変化なので、
$${\sqrt{1+(y´+δy´)^2}}$$をy’の関数として見た時に(y’,$${\sqrt{1+(y´)^2}}$$)を通る直線と近似するが出来ます。これをテイラー展開と呼ぶのですが、直線の傾きは$${\frac{d}{dx}\sqrt{1+(y´)^2}=\frac{(y´)^2}{\sqrt{1+(y´)^2}}}$$なので、
$${\sqrt{1+(y´+δy´)^2}}$$≃$${\sqrt{1+(y´)^2}+\frac{y´}{\sqrt{1+(y´)^2}}δy´}$$
と近似してあげることが出来ます。これを用いて、
$${δL[y(x)]=\int^a_0\frac{y´}{\sqrt{1+(y´)^2}}δy´dx}$$
が得られ、これは$${δy´=\frac{d}{dx}δy}$$なので部分積分することで、
$${δL[y(x)]=-\int^a_0\frac{d}{dx}\frac{y´}{\sqrt{1+(y´)^2}}δydx}$$
が得られます。(両端を固定しているのでδy(0)=δy(a)=0であり、部分積分した第一項が$${[\frac{y´}{\sqrt{1+(y´)^2}}δy´]^a_0=0}$$となるため)
これにより、任意のδyに対してδF=0となるには
$${\frac{d}{dx}\frac{y´}{\sqrt{1+(y´)^2}}=0}$$
となる必要がある事が分かります。$${y´(=\frac{dy}{dx})}$$がある一定の値の時にδLが0になり、Lが極値(ここでは最小値)を取る事が示されます。y´が一定値になるグラフとはつまり直線の事であり、ここではOAを繋ぐ直線であるy=0がOAを繋ぐ線の中で最短であることが示されます。
このような変分法と呼ばれる考え方を用いることで、最速降下問題に答える事も出来ます。
それでは、以下の形の汎関数についての変分問題を考えたいと思います。
物理学では位置xに対して時間tを変数として変化させることが多いため、yの代わりにxを、xの代わりにtを用いました。
$${S[x(t)]=\int^{t_1}_{t_0}L(x(t),x'(t))dt}$$
関数x(t)をx(t)+δx(t)に変化させたときの汎関数S[x(t)]の変分は、
$${δS=S[x+δx]-S[x]=\int^{t_1}_{t_0}{L(x+δx,x'+δx')-L(x,x')}dt}$$
であり、L(x+δx,x'+δx')をテイラー展開すると、
$${L(x+δx,x'+δx')=L(x,x')+\frac{∂L}{∂x}δx+\frac{∂L}{∂x'}δx'}$$
となるので、これを代入して、
$${δS=\int^{t_1}_{t_0}{\frac{∂L}{∂x}δx+\frac{∂L}{∂x'}δx'}dt}$$
ここで、右辺の第二項は$${δx´=\frac{d}{dt}δx}$$なので部分積分することで、
$${\int^{t_1}_{t_0}\frac{∂L}{∂x'}δx'dt=-\int^{t_1}_{t_0}\frac{d}{dt}(\frac{∂L}{∂x'}δx)dt}$$
が得られます。(両端を固定しているので$${δx(t_0)=δx(t_1)=0}$$であり、部分積分した第一項が$${[\frac{∂L}{∂x'}δx]^{t_1}_{t_0}=0}$$となるため)
以上より、変分δSは
$${δS=\int^{t_1}_{t_0}{\frac{∂L}{∂x}-\frac{d}{dt}(\frac{∂L}{∂x'})}δydt}$$
と書けます。任意のδx(t)に対して変分δSがゼロとなるための条件は、
$${\frac{∂L}{∂x}-\frac{d}{dt}(\frac{∂L}{∂x'})=0}$$
であり、この微分方程式をオイラー・ラグランジュ方程式と呼びます。
ここで計算に用いた汎関数Sを物理学では作用と呼び、運動は作用と呼ばれる汎関数を最小にするような軌道に沿って実現されることを変分原理(最小作用の原理)と呼び、変分原理が成り立つように関数L(x,x')に適切な関数を設定することで、このオイラー・ラグランジュ方程式がニュートンの運動方程式にとって代わる事が出来るようになります。このような考え方を用いた力学を解析力学と呼んでいます。
例えば、先ほどの最小降下曲線をオイラー・ラグランジュ方程式から導き出したいと思います。
まず、原点Oから点P(a,b)まで向かう途中の速さはy座標にのみ依存し、エネルギー保存から速さ$${v=\sqrt{2gy}}$$と与えられます。
先ほど求めたある関数y(x)のグラフの長さが$${\int^a_0\sqrt{1+(\frac{dy}{dx})^2}dx}$$であることを用いて、OからPまで到達する時間Tは
$${T[y(x)]=\int^a_0\sqrt{\frac{1+(\frac{dy}{dx})^2}{2gy}}dx=\int^a_0\sqrt{\frac{1+(y')^2}{2gy}}dx}$$
これをオイラー・ラグランジュ方程式$${\frac{∂L}{∂x}-\frac{d}{dt}(\frac{∂L}{∂x'})=0}$$に当てはめるためにオイラー・ラグランジュ方程式のxをyにtをxに置き換えて、
$${L=\sqrt{\frac{1+(\frac{dy}{dx})^2}{2gy}}}$$として、
$${\frac{∂}{∂y}\sqrt{\frac{1+(\frac{dy}{dx})^2}{2gy}}-\frac{d}{dx}(\frac{∂}{∂y'}\sqrt{\frac{1+(\frac{dy}{dx})^2}{2gy}})=0}$$
これを解くために、Lの全微分を考えます。
$${dL(y,y')=\frac{∂L}{∂y}dy+\frac{∂L}{∂y'}dy'}$$
両辺をdxで割って変形すると、
$${\frac{dL}{dx}-\frac{∂L}{∂y'}\frac{∂y'}{∂x}=\frac{∂L}{∂y}y'}$$
また、オイラーラグランジュ方程式にy'を掛けたものを考えます。
$${y'\frac{∂L}{∂y}-y'\frac{d}{dx}(\frac{∂L}{∂y'})=0}$$
二式より、$${\frac{∂L}{∂y}y'}$$を消去して、
$${\frac{d}{dx}(L-y'\frac{∂L}{∂y'})=0}$$
より、$${L-y'\frac{∂L}{∂y'}=(一定)}$$
ここに先ほどのLを代入すると、
$${\sqrt{\frac{1+y'^2}{2gy}}-y'(\frac{y'}{\sqrt{2gy(1+y'^2)}})=\frac{1}{\sqrt{2gy(1+y'^2)}}=A}$$
ここで、Aは定数なので、$${\frac{1}{2gA^2}=2C}$$とおいて、
$${y{1+(\frac{dy}{dx})^2}=2C}$$
この式は先ほどの最速降下問題の時にサイクロイドを解に持つ微分方程式に一致します。
また、保存力以外の力が働いていない物体の運動について記述する場合、関数L(x,x')はラグラジアンと呼ばれており、ラグラジアンLは
$${L=T-U}$$
と書けます。Tは物体の持っている運動エネルギーであり、Uは物体が持っている位置エネルギーです。
章末問題
[問2-1]トルリョチャギの際に蹴り脚側の腕を振る物理学的理由を考察しなさい。
[解2-1]「運動量保存により蹴り脚の運動量が増える」
この状態を理解しやすくするために、質量mと質量Mの2物体が二つバネにつながっている状態を考えてみたいと思います。

この2つの物体が左向きに同じ速度vを持ち、バネが縮んでいる状態を考えましょう。これは、回し蹴りでいうところの膝を抱え込んで相手に回し蹴りを当てようとしている状態を模式的に示した物になります。

蹴り脚を伸ばす動作は縮んだバネが伸びる動作に相当します。例えば、バネが伸びることで物体mの物体(蹴り脚に相当)は左向きに力を受けてさらに加速し、物体M(蹴り脚以外に相当)は右向きに力を受けて減速します。
この時、計算結果を分かりやすく示すため、物体Mの速度が左向きにvから0まで減速した場合について考えてみましょう。
まず、運動量保存を左向きを正として立てると、バネが伸びた後の物体m(蹴り脚)の速度をVとして、
$$
mv+Mv=mV+0
$$
が得られるので、$${V=\frac{M+m}{m}v}$$となります。つまり、Aの速度が$${V=\frac{M+m}{m}v}$$倍になりBの速度が0となります。
この時、身体全体が持っている運動エネルギー$${\frac{1}{2}mv^2}$$について計算してみると、
もともとの運動エネルギーは、
$$
\frac{1}{2}mv^2+\frac{1}{2}Mv^2=\frac{1}{2}(m+M)v^2
$$
であり、バネが伸びた後の運動エネルギーは、
$$
\frac{1}{2}m(\frac{M+m}{m}v)^2=\frac{M+m}{m}×\frac{1}{2}(m+M)v^2
$$
となるので、もともとの運動エネルギーから$${\frac{M+m}{m}}$$倍だけ増えているのが分かります。(m,M>0より$${\frac{M+m}{m}>1}$$)
この計算は、蹴り脚以外の部位を筋力発揮(筋肉の収縮。バネの伸び縮みに対応)による内力(体内部で相互に及ぼしあう力。床反力と重力以外の力)によって蹴り脚と逆回転方向にブレーキを掛けることで蹴り脚が加速し、蹴り全体の運動エネルギーが増加することが示唆されています。
トルリョチャギの際に蹴り脚側の腕を振る動作は腕がつながっている肩関節を通して上半身に対してブレーキを掛ける方向に運動依存力として作用しますから、結果的に蹴り全体の運動エネルギーを増加させる方向に働いていると言えるでしょう。
[問2-2]540度蹴りやターン蹴りなど空中での回転中に力学的エネルギーは保存するか否か答えなさい
[解2-2]
回転蹴りなど空中で回転する選手の慣性モーメントを$${I_1}$$、角速度を$${ω_1}$$とすると、角運動量は$${I_1ω_1}$$と書けます。ここで、手を開くと、選手の慣性モーメントが変化し$${I_2}$$となります。この時の角速度を$${ω_2}$$とすると、角運動量は$${I_2ω_2}$$と書けます。
選手が空中で受ける外力は重力のみなので、重力の作用点である重心を通る回転軸周りの運動量は変化しません。したがって、空中に居る選手全体の角運動量は保存するので、
$$
I_1ω_1=I_2ω_2
$$
となります。これを変形すると、変化後の角速度は、
$$
ω_2=\frac{I_1}{I_2}ω_1
$$
と得られます。
$${I_1>I_2}$$ならば、$${ω_2>ω_1}$$となるので、手を閉じるなどして慣性モーメントを小さくすれば、角速度が増えます。
一方で、回転のエネルギーについて計算すると、変化前のエネルギーは$${\frac{1}{2}I_1ω_1^2}$$であり、変化後のエネルギーは$${\frac{1}{2}I_2ω_2^2}$$となります。変化後のエネルギーについて先ほど得られた角速度を代入して計算すると、
$$
\frac{1}{2}I_2ω_2^2=\frac{1}{2}I_2(\frac{I_1}{I_2}ω_1)^2=\frac{1}{2}I_1ω_1^2×\frac{I_1}{I_2}
$$
となり、これは変化前のエネルギー$${\frac{1}{2}I_1ω_1^2}$$と一致せず、慣性モーメントを小さくすることで回転のエネルギーも増える事が計算できます。
この力学的エネルギーの増加の原因は何でしょうか?
外力である重力の仕事は全て並進運動の運動エネルギーの変化になるため、回転エネルギーを増やす事はありません。回転エネルギーの増加は筋収縮による内力の仕事によるものです。これは筋肉に蓄えられていた化学エネルギーが筋肉の収縮を通して回転エネルギーへと変換されたと言い換える事が出来ます。二つのエネルギーの差は
$$
\frac{1}{2}I_1ω_1^2×(\frac{I_1-I_2}{I_2})
$$
と計算できます。これは、慣性モーメントを小さくすれば小さくするほど大きくなる事を示しています。逆に慣性モーメントを大きくした場合にはこの値が負になります。(この時、筋肉がブレーキを掛ける事で回転のエネルギーは筋肉や骨格へと流入する為、筋肉や骨格は本当に微細なダメージを受けることになります)
この様に人体の運動中には筋収縮に伴うエネルギーの変化がある為、多くの場合で力学的エネルギー保存は成立しません。
2-14 力のモーメント(トルク)※執筆中
小学校・中学校の理科で学んだあとに高校物理で消える概念として「テコの原理」というものがあります。てこの原理は、力点に力を加え、支点を中心とした回転運動により、作用点に大きな力を加えることができる原理です。変形しない棒(剛体棒)を始点を中心に回転させる為に、棒に対して力点に下向きの力を加えることで、棒がおもりに対して上向きの力を及ぼし、その力の大きさは作用点と力点の始点からの距離の逆比となります。
したがって、支点から作用点までの距離を1とし、支点から力点までの距離をxとすると、力点で棒に加えた下向き力Fのx倍の力xFを棒がおもりに対して上向きにおよぼす力になります。
てこの原理は棒が受ける力のモーメントのつりあいから説明する事が出来ます。力のモーメントのつりあいを立てる時は注目する物体を決めて、その物体に働く力を全て図示する必要があります。ここでは回転する物体である剛体棒に働く力を全て書き出して考えてみたいと思います。
$${F_1}$$


第3章 各種蹴り技についての物理学的考察(執筆中)

3-1 前蹴りを上足底で蹴る物理学的な理由

前章の第1章第12節「打撃を単振動でモデル化する」では打撃の威力を定義する圧力の最大値は次のような数式に近似できる事を物理学的に説明しました
$$
P_{max}=\frac{v}{S}\sqrt{mk}=\frac{1}{S}\sqrt{2kE}
$$
この数式中で、Sは打撃の接触面積、Eは打撃部位の運動エネルギーを示しており、kは打撃部位の外力による変化のし難さを外力F[N]÷外力による変形x[m]で表した係数(人体をバネとみなした時のバネ定数)になります。
数式から分かる事は、Sを小さくすればするほど、Eとkを大きくすればするほど威力が上がる事が分かります。
例えば、前蹴り(アプチャギ)の場合、足の裏全体で蹴るよりも上足底(アプクンチ)で蹴る事で蹴りの接触面積Sを小さくする事が出来ます。
その一方で上足底で蹴る場合には足の裏全体で蹴る場合よりも足首関節の変形の影響も無視できず、ヒット時に足首を固めて蹴らなければkが小さくなってしまいます。そこで、上足底を用いた前蹴りの場合には蹴り足の足首を曲げずに伸ばし、クッションとなってしまう事を防ぐ必要があります

3-2 540度蹴りの物理学的なコツ
WTテコンドーの演武で最も基本的な蹴りの一つが540度蹴りです。XMAやトリッキングの界隈では蹴り脚着地のターン蹴りを540度と呼ぶため、チート720度とも呼ばれています。
この540度蹴りを蹴り切るための必要なことを物理学的に考えると、大きく分けて二つの事が必要になります。
1.高く跳ぶこと
2.踏切までに十分な回転を作ること
一つ目の「高く跳ぶこと」というのは多くの人にとって当たり前の話かもしれませんが、物理学的に考えて高く跳べば跳ぶほど滞空時間が長くなります。スーパーマリオUSAというゲームに出てきたピーチ姫のような、低いけど滞空時間が長いジャンプというのは物理学的には不可能です。
漫画スラムダンクでは桜木花道のジャンプは滞空時間が長いと描写されていましたが、これが現実世界の選手ならば、最高到達点も同時に高くなります。
理由は簡単で、空中に居る人体が受ける力は重力のみになる為です。人間の身体が受ける重力の大きさは質量$${m}$$のみに比例し、重力加速度$${g}$$との積$${mg}$$と書けます。力とは物体に加速度を生じさせる原因なので、この重力が原因となって空中に居る物体には下向きに$${g}$$の加速度が生じます。
人間のジャンプは踏切り直後の上向きの初速度$${v_0}$$が重力加速度$${g}$$によって減速し、速度が0になるまで身体(の重心)が上昇を続け、そのあとは下向きの速度が重力加速度$${g}$$で加速しながら落下していきます。踏切りの瞬間を$${t=0}$$とした場合、ある時刻$${t}$$における速度$${v(t)}$$は
$$
v(t)=v_0-gt
$$
と書けます。例えば、踏切り直後から最高到達点に達するまでの時間を$${T}$$として、この式に代入すると、最高点の速度$${v(T)=0}$$なので、$${0=v_0-gT}$$という関係式が成り立ち、これを変形すると$${T=\frac{v_0}{g}}$$が得られます。一般的に滞空時間はこの最高到達点に達するまでの時間$${T}$$を2倍した値となります。
速度というのは単位時間(1秒)当たりの位置の変化であり、時間を掛けることで移動距離が計算できるのですが、今回の様に速度が常に変化し続ける場合は単に時間を掛けるだけでは移動距離を計算する事が出来ません。
しかし、速度の変化が無視できるくらい微小な時間$${dt}$$の間の移動距離であれば、これを$${vdt}$$と書いてあげる事が出来ます。
そして、この$${vdt}$$をt=0~t=Tまでの間で足し合わせてあげることで最高到達点の高さ$${h}$$を計算することができます。
このような微小な時間を掛けた値を足し合わせる事を時間積分と呼びます。試しに、速度vを時間積分して高さを求めると、次のような計算になります。
$$
h=\int^T_0(v_0-gt)dt=v_0T-\frac{1}{2}gT^2
$$
ここで、$${T=\frac{v_0}{g}}$$を用いて、初速度を消去すると、最高点に達するまでの時間は
$$
T=\sqrt{\frac{2h}{g}}
$$
と得られ、滞空時間が$${2T=2\sqrt{\frac{2h}{g}}}$$であることから「高く跳ぶこと」で滞空時間を長くできることが示されます。偉そうに数式を使って書きましたが、当たり前の事を確認しただけなので「馬鹿でも分かることを難しく書く馬鹿」になってしまっていますが悪しからず。
本題は二つ目の「踏切までに十分な回転を作ること」という部分になります。物理学では回転の大きさを表すための物理量として、回転エネルギーと角運動量の二つがあります。
回転エネルギーとは回転運動の運動エネルギーの事を意味しています。

例えば、上図の様に質量mの物体が回転している場合の運動エネルギーは物体の速度$${v}$$を用いて、$${E=\frac{1}{2}mv^2}$$と書けるのですが、単位時間(1秒)あたりの回転角度である角速度$${ω}$$と半径$${r}$$の積が物体の速度$${v}$$になる事を用いると、$${E=\frac{1}{2}mr^2ω^2}$$とも書けます。此処で、質量×半径の二乗である$${mr^2}$$を慣性モーメントと呼び、$${I=mr^2}$$であらわされるとすれば、回転エネルギーは
$$
E=\frac{1}{2}Iω^2
$$
と書けます。慣性モーメントが大きいほど、同じ角速度の回転でもエネルギーが大きくなることから、慣性モーメントは物体の回転しにくさを表しています。物体は質量が大きければ大きいほど、回転半径が大きければ大きいほど慣性モーメントが増して回転しにくくなります。
一方、ニュートンの運動方程式$${ma=F}$$は速度と加速度の数学的な関係である$${a=\frac{dv}{dt}}$$を用いて、
$$
m\frac{dv}{dt}=F\\
mr\frac{dω}{dt}=F\\
mr^2\frac{dω}{dt}=r×F\\
I\frac{dω}{dt}=r×F
$$
と書くことができます。此処で、最終的に出てきた$${r×F}$$は物理用語で力のモーメントと呼ばれている物で、一般的にはトルクと呼ばれ、物体の回転を変化させる原因となる物理量です。ニュートンの運動方程式$${m\frac{dv}{dt}=F}$$のFが速度を変化させる原因とするならば、回転の運動方程式$${I\frac{dω}{dt}=r×F}$$の$${r×F}$$は角速度を変化させる原因となります。rは半径、Fは力です。
空中にある物体は必ず重心を通る回転軸回りに回転しますから、重力によるモーメント(トルク)は空中では必ず0になってしまいます。
つまり、空中では回転の運動方程式は、
$$
I\frac{dω}{dt}=0\\
\frac{d}{dt}Iω=0\\
$$
この式はつまり、空中では慣性モーメントと角速度の積$${Iω}$$の大きさが変化しないという事を示しています。ここで$${Iω}$$の事を角運動量と呼び、外からトルクを受けてない物体の角運動量が変化しないことを角運動量保存の法則と言います。したがって、重力以外の外力(床反力)を受けることができる踏切りまでの段階で作った角運動量がそのまま空中姿勢における角運動量と変らない事が分かります。このことから、540度を蹴る為には踏切までに十分な回転を作ることが大切であることが分かります。
3-3 上段蹴りと中段蹴りの違いについて(執筆中)
2-6 相対運動を考えた衝撃力の近似計算では打撃の衝撃力は次のように近似できる事を示しました。
$$
F_{max}≒\frac{2mM(1+e)(v-V)}{(m+M)⊿t}
$$
また、衝撃力による力積Iは
$$
I≒\frac{F_{max}⊿t}{2}
$$
とも近似できる事を示しました。これらの式を用いて幾つかの事を考察したいと思います。
先ず、衝撃力の最大値をターゲットの質量Mで偏微分してみましょう。
$$
\frac{∂}{∂M}F_{max}≒\frac{2m^2(1+e)(v-V)}{⊿t}\frac{1}{(m+M)^2}>0
$$
より、Mが増加する事で、$${F_{max}}$$は単調増加となる事が分かります。一方で、Mを増加させる事で偏導関数$${\frac{∂}{∂M}F_{max}}$$は分母が増加していく事から常に減少していき、$${\lim_{M \to \infty}\frac{∂}{∂M}F_{max}=0}$$となる事から、
$$
\lim_{M \to \infty}F_{max}≒\frac{2m(1+e)(v-V)}{⊿t}
$$
となる事が分かります。例えば、打撃部位の質量m=10kgとし、打撃の速度v=10m/s、(運動エネルギー$${\frac{1}{2}mv^2=5.0×10^2[J]}$$)ターゲットの速度V=0m/s、衝突時間を10ミリ秒、反発係数e=0とした場合の衝撃力の最大値$${F_{max}}$$はターゲットの質量Mに対して次のようなグラフが書ける事が分かります。

今度は同じ運動エネルギーでも質量を5.9[kg]まで軽くし、代わりに速度を13[m/s]とした場合について計算してみたいと思います。この条件でグラフを書いた場合、次の様なグラフが得られます。
青線が元々のグラフ。オレンジ線が同じエネルギーで質量を小さくした場合のグラフですが、ターゲットの質量が小さい範囲では打撃部位の質量も小さいオレンジ線が衝撃力の最大値が大きくなり、ターゲットの質量が大きくなると打撃部位の質量が大きい青線の衝撃力の最大値が大きくなる事が示されます。

しかし、既存の指導方法である「頭部の様な質量の小さい部位を攻撃する時は速い打撃の方が有効」という結果を示すほどの物ではありません。
これは接触時間⊿tの質量依存について考察していなかった為と考えられます。例えば、衝突を単振動モデルで考えた場合、⊿tは二物体の換算質量の二乗根に比例し、
$$
⊿t∝\sqrt{\frac{mM}{(m+M)}}
$$
と書く事が出来ます。そこで、比例定数Kを置いて、
$$
⊿t=K\sqrt{\frac{mM}{(m+M)}}
$$
と、仮定してみましょう。この⊿tを代入した、
$$
F_{max}≒\frac{2(1+e)(v-V)}{K}\sqrt{\frac{mM}{m+M}}
$$
に対して、m=10kg、M=10kgで⊿t=10ミリ秒となる様にKの値を定めて、
m=10kg、v=10m/s(オレンジ線)、m=5.9kg、v=13m/s(青線)でシミュレーションをすると、結果は下の図のように得られてしまいます。

このシミュレーションからは同じエネルギーの打撃ならば速度を速くして質量を軽くし力積が小さいほうがターゲットの質量とは関係なく衝撃力の最大値が大きい事が示されます。
「重い部位には重い打撃。軽い部位には軽いが速い」という従来のセオリーが上手く顕れません。おそらく、このシミュレーションには⊿tの質量依存を単純化し過ぎたという欠陥がありそうです。
【参考文献】
[補講②]
大山卞圭吾「アスリートのための解剖学」(草思社)
[2-9、2-10]
武道・スポーツの基礎となる棒の力学:特に慣性力の重要性
