微分係数

今回使うグラフは下のものです。

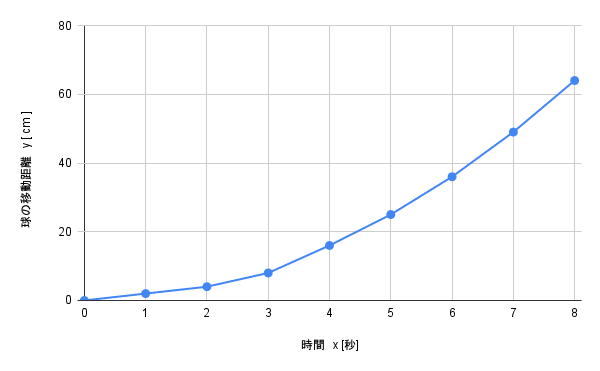
x = 0からx = 8までの区間を見ると直線的に増えていません。
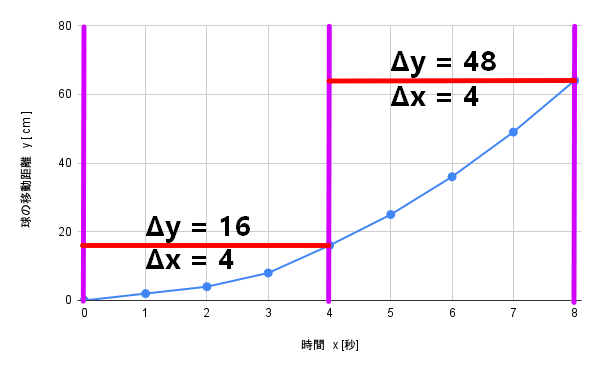
x = 0からx = 4とX = 4からx = 8のそれぞれを分けてみます。

$$
前半は \frac{Δy}{Δx} = 4,後半は \frac{Δy}{Δx} =14
$$

このように直線的に増えてなくて
前半は少なくて、後半は多めになっています。

Δxをさらに細かくするとこうなります。

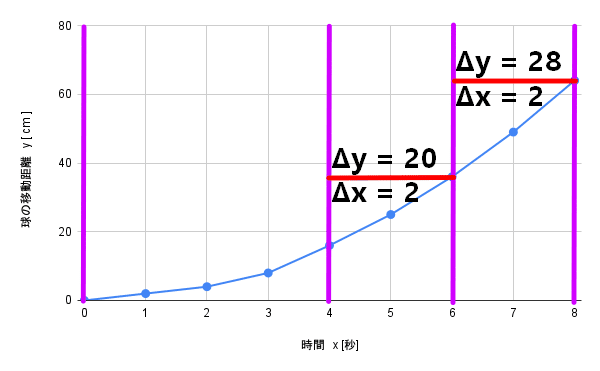
x = 4からx = 6までは

$$
\Delta x = 2,\Delta y = 20なので \frac{\Delta y}{\Delta x} = \frac{20}{2} = 10
$$

x = 6からx = 8までは

$$
\Delta x = 2,\Delta y = 28なので\frac{\Delta y}{\Delta x} = \frac{28}{2} = 14
$$

やはり前半は少なくて、後半は多めになっています。

Δxの範囲を小さくするとΔyの値も変化します。
その変化を式にしていく前に求め方を考えます。

グラフのもとになる式は
y = (xの出てくる式)の形で書かれることが多いです。

xによってyの値が決まるので、yはxの関数 function of xとなり
y = f( x )と表せます。

f( )の中にあるxに実際のxの数値を入れてみます。
x = 1のときのyの値：y = f( 1 )
x = 2のときのyの値：y = f( 2 )
x = 3のときのyの値：y = f( 3 )
x = 3.1のときのyの値：y = f( 3.1 )
x = 3 + Δxのときのyの値：y = f( 3 + Δx )

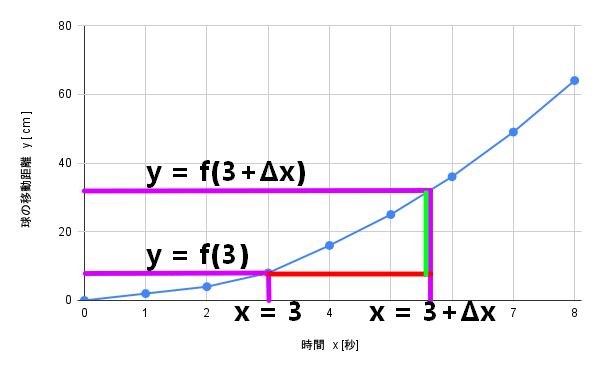
xが3から3+Δxまで増加したときに
yはf( 3 )からf( 3+Δx )増えているので

Δy = f( 3+Δx ) - f( 3 )になります。
つまり増加率は

$$
増加率 \frac{\Delta y}{\Delta x} = \frac{f( 3 + \Delta x ) - f( 3 )}{\Delta x}
$$

と書くことができます。

それではΔxの範囲を小さくしていきたいと思います。
「Δxを極限まで0に近づけていく」という意味で
Δx -> 0の極限[リミット、limit]として次のように書きます。

$$
\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim \limits_{\Delta x \to 0} \frac{f(3+\Delta x) - f(3)}{\Delta x}
$$

$$
これを「x = 3における微分係数」と呼んで\\「f^{\prime}(3)」と書きます。
$$

つまりこのように書き換えることができます。

$$
f^{\prime}(3) = \lim \limits_{\Delta x \to 0} \frac{f(3+\Delta x) - f(3)}{\Delta x}
$$

$$
余談ですが、f^{\prime}を日本ではfダッシュと読む人が多いようですが\\英語ではfプライムと読みます。
$$

「x = 5における微分係数」は

$$
f^{\prime}(5) = \lim \limits_{\Delta x \to 0} \frac{f(5+\Delta x) - f(5)}{\Delta x}
$$

になります。

ほかの例を1つ見てみます。
「x = 2における微分係数」は

$$
f^{\prime}(2) = \lim \limits_{\Delta x \to 0} \frac{f(2+\Delta x) - f(2)}{\Delta x}
$$