
第9章 信用連関会計恒等式(AICI)モデル
9.1 分析の目的
従来のマクロ経済学、特に経済成長論やRBC(Real Business Cycle)モデルの領域では、金融部門の存在と活動が排除されていた。しかし、本稿のこれまでの議論の中で、SNAの勘定科目体系とその相互間の勘定連絡(会計恒等式)を通じて、マネーストック変動額(ΔM)、貯蓄(S)、投資(I’)、資本蓄積(ΔK)等が相互に有機的に連関していることを証明した。
本章の目的は、信用連関会計恒等式(AICI: Accounting Identity of Credit Interlinkage)モデルの分析枠組みにより、地価・株価といった資産価格バブルの発生と崩壊という外的ショックが、信用連関(Credit Interlinkage)としての金融資産・負債の膨張と収縮にどのように影響するのか、そして最終的に一国経済全体の資本(K)、すなわち国富に対して及ぼすダイナミックな乗数効果を定量的に測定・分析することにある。また、そのような外的ショックに対し、政府による公共投資や事業会社による設備投資を金融機関からの借入(Debt finance)により実施した場合、あるいは政府による不良債権買取と中央銀行による金融機関への資本注入を組み合わせた直接的な不良債権処理策を実施した場合に、一国経済全体の金融資産・実体資産、負債、そして資本(国富)にいかなる影響を及ぼすか、についてもシミュレーションと分析を実施する。
加えて、本章では、海外部門において、新たな国際機関としてケインズ型のアジア決済同盟(仮称、CUA: Clearing Union of Asia)を各国政府の出資により設立の上、中央銀行間のネットワークで貿易決済等の運用を行った場合、一国経済全体の資本(国富)や経済成長にいかなる影響をもたらすか、シミュレーションと分析を実施する。とりわけアジア決済同盟(CUA)が資本として発行する暗号資産(Blockchain Equity)だけでなく、貿易決済等を目的として加盟各国中央銀行に提供する同暗号資産建の準備預金(Blockchain Reserve)を導入した場合、一国経済全体の金融資産・実体資産、負債、そして資本(国富)にいかなる影響を及ぼすか、についてもシミュレーションと分析を実施する。
9.2 分析方法
会計恒等式の動的モデル化
会計恒等式を基盤とするマクロ経済モデルの特徴は、特定時点でのストック変数(資産/負債/資本等の残高)と特定期間のフロー変数(GDP/消費/投資/純輸出/貯蓄等の取引高)が相互に影響し合いつつ数学的に同時決定されるという恒等関係にある。つまり、会計恒等式が表現するのはマクロ変数相互間の静的(static)な関係であり、そのままでは経済成長や財政・金融政策の効果といった時間的要素を伴う動的(dynamic)なマクロ変数の変化を表現することはできない。
そこで、静的(static)な会計恒等式を動的(dynamic)なマクロ経済モデルに拡張するため、レオンチェフ逆行列の数学的処理を活用する。それは経済の各時点での静止画像をつなぎ合わせることで、経済の動的な流れを捉えるアプローチともいえる。レオンチェフ逆行列により、地価・株価といった実体資産の価格変動による金融資産・負債、そして資本(国富)への乗数効果を測定することに加えて、経済成長や財政・金融政策の効果といった時間的要素を伴う動的(dynamic)なマクロ変数の変化を表現することが可能となる。
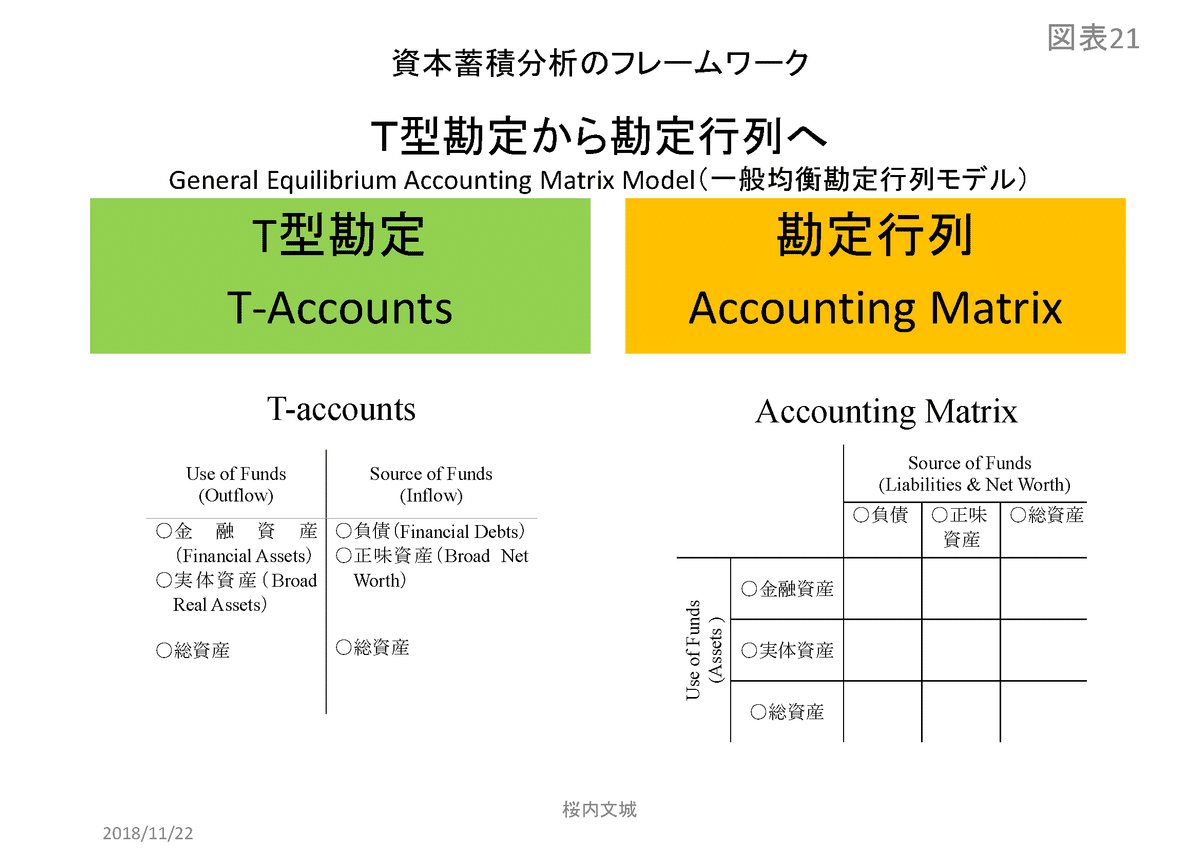
従来、レオンチェフ逆行列は、SNAの2.国内総生産勘定を行列化した産業連関表において、投入・産出分析(Input/Output Analysis)を行うため、レオンチェフ(Leontief W.)によって開発されたものである。本章ではこれを応用し、SNA上の金融部門による過去の活動の蓄積ともいえる5.金融勘定の金融資産・負債を制度部門別に行列化した。これを「金融勘定行列」と呼ぶ。その上で、1.貸借対照表勘定上の(借方)実体資産(土地/生産資産/株式)を制度部門別にベクトル化すると共に、(貸方)資本(国富)についても制度部門別にベクトル化した。
T型勘定(T-Account)から勘定行列(Accounting Matrix)への変換
本章以前の各章では、複式簿記の貸方(右側)と借方(左側)から成るT型勘定(T-Accounts)にSNAを組替えて分析を行ってきた。この第4部では、地価・株価といった実体資産の価格変動による金融資産・負債、そして資本(国富)への乗数効果を測定することを目的として、SNAのT型勘定(T-Accounts)による1.貸借対照表勘定と5.金融勘定を基礎として、これらを更に2次元の勘定行列(Accounting Matrix)に組替える。
信用連関会計恒等式(AICI)モデル
単純化のため、SNAの制度部門に倣い、政府、中央銀行、金融機関、非金融法人企業(事業会社)、家計、そして海外という6つの制度部門に整理した。
なお、SNAにおいて中央銀行は「金融機関」の一つとして位置付けられているが、2013年に開始された「異次元緩和」の影響により、執筆時点(2019年3月)で日銀の保有する国債(資産)と日銀当座預金(負債)が両建てで400兆円近く膨張したことに配慮し、一般の「金融機関」とは別に一つの制度部門として位置付けることとした。
他方、制度上、銀行(預金取扱機関)とその他の金融仲介機関とは、信用創造機能の有無で区別される。しかし、2007-2008年の世界金融危機以降、投資銀行(証券会社)、ヘッジファンドの他、証券化のための特殊な運用会社等を意味する「シャドーバンキング・システム」の発行する多種多様な負債は、銀行(預金取扱機関)の負債であるマネーストック(M)との区別すら曖昧にしている。例えば、MMF(Money Market Fund)、レポ取引(現金担保付債券貸借取引)の他、資産担保証券(ABS: Asset Backed Securities)、ABSを束ねて更に証券化したCDO(Collateralized Debt Obligation)、そしてCDOの保険としてのCDS(Credit Default Swap)等が「シャドーバンキング・システム」の負債である。実際、世界金融危機の最中、2008年9月に米国のFRB(連邦準備理事会:Federal Reserve Board)がMMFの保有するASCP(Asset Backed Commercial Paper)を買い取り、銀行預金保護と同様の支援をして以降、MMFも銀行預金(マネーストック)と変わらぬ通貨としての機能を有するようになっている。そこで、本章では、銀行(預金取扱機関)とその他の金融仲介機関とを敢えて区別せず、「金融機関」という一つの制度部門として位置付けることとしている。
その上で、原則として日銀が作成している①資金循環統計「金融資産・負債残高表」、②国際収支統計「本邦対外資産負債残高」及び③日銀自体の決算数値を基に勘定行列(Accounting Matrix)の各セルの数値を埋めていく。なお、政府、金融機関、事業会社及び家計の実体資産(土地/生産資産/株式)に関する4つのセルについては、財務省「国の財務書類(一般会計・特別会計)」及びSNAストック編制度部門別貸借対照表から数値を導いている。
本稿では、これを「BS勘定行列」と呼ぶ。また、BS勘定行列を基礎とする分析の枠組みを「信用連関会計恒等式(AICI: Accounting Identity of Credit Interlinkage)モデル」と呼ぶ。

金融係数行列への標準化
$${\tilde{L_f}}$$: 負債係数行列(Liability Coefficients Matrix)

BS勘定行列(図表23)においては、後述の国際的な貿易等に関するケインズ型決済同盟(CUA: Clearing Union of Asia)を設立・運営する場合に発行されるデジタル通貨(Bancor)建の金融資産・実体資産、負債及び資本(国富)のセルも追加している。
さて、BS勘定行列(図表23)の最下段の「縦合計(総資産)」の行の各セルの数値で、同じ列にある各制度部門別の負債の数値を除する(割り算する)ことにより、 (負債係数行列)が得られる。

そして、SNAの1.貸借対照表勘定の貸方(右側)において、次の貸方勘定恒等式(Credit Account Identity)が常に必ず成立する(図表23及び図表24参照)。
$${\tilde{A_f}}$$: 金融資産係数行列(Financial Asset Coefficients Matrix)
次に、上記BS勘定行列(図表23)における行と列を入れ替えた転置行列も作成する。本稿では、これを「BS勘定転置行列」(図表25)と呼ぶこととする。なお、BS勘定行列(図表23)の場合と同様、BS勘定転置行列(図表25)においても、後述の国際的な貿易等に関するケインズ型決済同盟(CUA: Clearing Union of Asia)を設立・運営する場合に発行されるデジタル通貨(Bancor)建の金融資産・実体資産、負債及び資本(国富)のセルも追加している。

BS勘定転置行列(図表25)の最下段の「縦合計(総資産)」の行の各セルの数値で、同じ列にある各制度部門別の金融資産の数値を除する(割り算する)ことにより、 (金融資産係数行列)が得られる。

そして、SNAの1.貸借対照表勘定の借方(左側)において、次の借方勘定恒等式(Debit Account Identity)が常に必ず成立する(図表25及び図表26参照)。
9.3 信用連関会計恒等式(AICI)モデルの設計思想
会計恒等式と勘定行列
産業連関分析(Input/Output Analysis)で用いられるレオンチェフ逆行列は、いわばSNA上の2.国内総生産勘定のフロー変数の会計恒等式を行列化したものである。これに対して、BS勘定行列及びBS勘定転置行列は、SNAの1.貸借対照表勘定における[借方]金融資産/実体資産(土地/生産資産/株式[1])、[貸方]負債/資本(国富)というストック変数の会計恒等式から成る勘定行列(Accounting Matrix)である。
ジャンプ変数と非ジャンプ変数
経済モデルの変数には、①経済モデルの連立方程式体系における未知変数であって、その連立方程式を解くことにより体系内で数値が決定される内生変数(endogenous variable)と,②体系外で数値が決定される外生変数(exogenous variable)がある。
なお、連立方程式を解いて内生変数の解を得るためには、方程式の数と内生変数の数が等しくなければならない。既に準備した金融資産係数行列($${\tilde{A_f}}$$)、負債係数行列($${\tilde{L_f}}$$)は共に6制度部門による6行6列行列という連立方程式であるから、それぞれ6つの成分(内生変数)から成る金融資産ベクトル($${\vec{A_f}}$$)、実体資産ベクトル($${\vec{R}}$$)、負債ベクトル($${\vec{L_f}}$$)、資本ベクトル($${\vec{K}}$$)、そして総資産ベクトル($${\vec{S}}$$)の解を得ることができる。
信用連関会計恒等式(AICI)モデルの設計・開発に際して、もう一つ留意すべきことがある。それは、金融資産係数行列($${\tilde{A_f}}$$)、負債係数行列($${\tilde{L_f}}$$)により構成される連立方程式の内生変数が「ジャンプ変数」または「非ジャンプ変数」のいずれか、という点である。
マクロ経済モデルにおける消費(C)、投資(I)等のフロー変数を「ジャンプ変数」と呼ぶことがある。フロー変数は、会計期間が異なれば全く異なる(ジャンプした)金額となってもおかしくないからである。従って、レオンチェフ逆行列が産業連関分析として扱うSNA上の2.国内総生産勘定のフロー変数は全て「ジャンプ変数(jump variable)」ということになる。従って、「ジャンプ変数」の外生変数の場合、その設定において内生変数相互間の関係性に配慮する必要はない。
これに対して、SNAの1.貸借対照表勘定における金融資産、実体資産(土地/生産資産/株式)、負債及び資本(国富)というストック変数から構成される信用連関会計恒等式(AICI)モデルの内生変数は、基本的に「非ジャンプ変数」である。「非ジャンプ変数」の内生変数の場合、互いが互いに依存する「reflexivity(再帰性/相互作用性)」の関係性が存在する。
また、ストック変数の変動と結び付けられるフロー変数も「非ジャンプ変数(non-jump variable)」となる。例えば投資(I')は一期間中のフロー変数ではあるが、同時に貸借対照表上の実体資産の期首と期末の間の変動(差額)でもある。同様に、貯蓄(S)も一期間中のフロー変数ではあるが、過去からの蓄積である資本(国富)の期首と期末の間の変動(差額)でもある。これらは数学的には「$${I'=S=dK/dt=\dot{K}}$$」という資本(K)ストックの時間微分とも表現される。
従って、信用連関会計恒等式(AICI)モデルの設計・開発に際しては、「非ジャンプ変数」である内生変数相互間の関係性ないし制約条件(規則)に留意なければならない。その制約条件(規則)とは、例えば、「非ジャンプ変数」である投資(I')と貯蓄(S)については、「資本(K)の期首残高+当期の投資(I'){=貯蓄[S]}=資本(国富)の期末残高」という、SNA上の会計恒等式(Accounting Identity)に従うことである。以下、シミュレーションでも用いる代表的な4つの例を示す。
【例1】国債発行による政府の公共投資(Ig)の場合
国債発行と公共投資(Ig)を行う政府
(借方)実体資産100
(貸方)(金融機関が引受・保有する)国債100
投資財を販売する事業会社
(借方)金融機関に対して保有する金融資産(マネーストック)100
(貸方)資本[利益剰余金]100
金融機関
(借方)(政府に対する金融資産として)保有する国債100
(貸方)事業会社に対する負債(マネーストック)100
【例2】事業会社が株式を上場した場合(家計による株式投資と仮定)
株式上場した事業会社
(借方)金融機関に対して保有する金融資産(マネーストック)150
(貸方)資本[資本金]150
その上で、この事業会社が資本として調達したEquity Financeによる投資を行った場合、以下の複式仕訳が発生する。
株式上場後、設備投資を行った事業会社
(借方)実体資産150
(貸方)金融資産(マネーストック)150
投資財を販売する事業会社
(借方)金融資産(マネーストック)150
(貸方)資本[利益剰余金]150
【例3】借入(Debt finance)による投資の場合
①借入時
金融機関
(借方)事業会社(貸付先)に対する金融資産(貸付金)200
(貸方)事業会社(貸付先)に対する負債(預金通貨=マネーストック)200
事業会社
(借方)金融機関に対して保有する金融資産(マネーストック)200
(貸方)金融機関に対する負債(銀行借入)200
②投資時
投資主体(銀行から借入をした事業会社)
(借方)実体資産200
(貸方)金融資産(マネーストック)200
投資財を販売する事業会社
(借方)金融資産(マネーストック)200
(貸方)資本[利益剰余金]200
【例4】金融危機における政府・中央銀行が実施する不良債権処理・金融機関への資本注入スキーム
①政府が国債300を発行し、これを対価として金融機関の不良債権300を買取った上で償却(費用化)する場合、以下の複式仕訳が発生する。
金融機関
(借方)(政府に対する金融資産として)保有する国債300
(貸方)事業会社(貸付先)に対して保有する金融資産(貸付金)300
政府
(借方)事業会社(貸付先)に対して保有する金融資産(貸付金)300
(貸方)(金融機関が引受・保有する)国債300
実際には、事業会社(貸付先)に対して保有する金融資産(貸付金)は200が不良債権化しており、簿価300に対して実際の価値は3分の1の100にまで下落したものと仮定する。政府が簿価300と等価の国債(最優良債券)300と交換することにより、金融機関側の不良債権処理は終了する。その後、政府は事業会社(貸付先)に対して保有する金融資産(貸付金)300のうち、200を償却(費用化)する。なお、政府会計(公会計)は現金主義であるから、政府は不良債権の償却(費用化)200を予算・決算上、認識する必要はない。
政府
(借方)不良債権の償却(費用化)200
(貸方)事業会社(貸付先)に対して保有する金融資産(貸付金)200
②次に、中央銀行が債券発行(金融機関による引受)により調達した資金で金融機関に対して資本注入を実施する場合、以下の複式仕訳が発生する。
中央銀行
(借方)金融機関に対する資本注入(実体資産)100
(借方)金融機関に対する中銀債発行100
金融機関
(借方)中銀債100
(借方)資本100
信用連関逆行列分析の構造
信用連関逆行列分析においては、会計恒等式の勘定行列を金融係数行列に標準化した上でレオンチェフ逆行列を求めることにより、会計恒等式の同時的な恒等関係を維持しつつ、マクロ変数相互間の時間的要素を含む因果関係を表現することが可能となる。
具体的には、ある観測可能変数(OV)[本稿では実体資産ベクトル ]を外生変数ベクトル、その他の観測可能変数(OV)及び残高調整項目(BI)を内生変数ベクトル/先決内生変数ベクトルと位置付け、会計恒等式の勘定行列の動的な変化を計算・測定する。外生変数ベクトルの入力により内生変数ベクトルの数値(出力結果)が一旦確定すると、それは先決内生変数(predetermined endogenous variables)として機能し、経済モデル内の他の変数ベクトルに影響を与える。つまり、先決内生変数ベクトルの確定により、それが他の内生変数ベクトルに影響を及ぼし、モデル全体の動的な挙動を形成する。この再帰的なフィードバックループは、経済の動的な変化を捉え、時間を通じた経済の挙動を表現するのに不可欠となる。
実体資産ベクトル の変動による総資産ベクトル 及び金融資産ベクトル への波及効果の測定
借方勘定恒等式 を変形することにより逆行列 を導出した上で、両辺に逆行列 ベクトルを左から乗ずることにより、総資産ベクトル を得ることができる。

以下、借方勘定恒等式 から導かれる逆行列 を便宜的に「信用連関逆行列(IMCI: Inverse Matrix of Credit Interlinkage)」と呼ぶこととする。
信用連関逆行列 を用いた演算 により、①実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$における地価や株価といった資産価格が変動した場合、または、②政府による公共投資や事業会社による設備投資により実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$における生産資産(Produced Assets)が増加した場合、実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$を外生変数として、先決内生変数である総資産ベクトル$${\vec{S}}$$に対する波及効果が測定可能となる。
また、借方勘定恒等式 を変形すると、上記のように金融資産ベクトル$${\vec{A_f}}$$も求められる。
これにより、①実体資産(土地/生産資産/株式)ベクトル$${\vec{S}}$$における地価や株価といった資産価格が変動した場合、または、②政府による公共投資や事業会社による設備投資により実体資産(土地/生産資産/株式)ベクトル$${\vec{S}}$$における生産資産(Produced Assets)が増加した場合、外生変数である実体資産(土地/生産資産/株式)ベクトル$${\vec{S}}$$と先決内生変数である総資産ベクトル$${\vec{S}}$$により、内生変数である金融資産ベクトル$${\vec{A_f}}$$に対する波及効果が測定可能となる。
実体資産ベクトル の変動による資本(国富)ベクトル 及び負債ベクトル への波及効果の測定
次に、借方勘定恒等式 について、信用連関逆行列 を用いて変形し、外生変数である実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$の数値(データ)を投入することで先決内生変数である総資産ベクトル$${\vec{S}}$$を求める$${(\tilde{I}-\tilde{A_f})^{-1}\vec{R}=\vec{S}}$$について、両辺の左側から資本(国富)係数行列$${\tilde{K}}$$を乗ずると、もう一つの先決内生変数である資本(国富)ベクトル$${\vec{K}}$$が得られる。
更に、貸方勘定恒等式 を変形すると、次のように内生変数である負債ベクトル も求められる。

これにより、①実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$における地価や株価といった資産価格が変動した場合、または、②政府による公共投資や事業会社による設備投資により実体資産(土地/生産資産/株式)ベクトル$${\vec{R}}$$における生産資産(Produced Assets)が増加した場合、内生変数である負債ベクトル$${\vec{L_f}}$$に対していかなる波及効果を及ぼすのか、測定可能となる。
特に、負債ベクトル$${\vec{L_f}}$$の成分のうち、(シャドーバンキングを含む)金融機関の負債はマネーストックを構成する。従って、実体資産(土地/生産資産/株式)ベクトル における資産価格の変動により、(シャドーバンキングを含む)金融機関の負債の変動、すなわちマネーストックの増加・減少にいかなる波及効果を及ぼすか、測定可能となる。
なお、負債ベクトル$${\vec{L_f}}$$の成分のうち、事業会社または家計の負債が減少するシミュレーション結果となる場合であっても、現実には金融機関による不良債権処理(貸倒引当金繰入による間接処理または債権回収による最終処理)がなされない限り、過剰債務として積み残されるのが通常である。その場合、総資産ベクトル の収縮の大きさに比べて負債ベクトル$${\vec{L_f}}$$の収縮の度合いが小さくなることから、過剰債務の分、資本(国富)ベクトル$${\vec{K}}$$がより毀損することとなる。

実体資産ベクトル の変動による資本(国富)ベクトル を通じた国民所得(Y)への波及効果の測定
上記恒等式 により、実体資産(土地/生産資産/株式)ベクトル の変動による資本(国富)ベクトル に対する波及効果を測定できる。従って、第5章で示した下記「国民所得方程式」により、翌期(t+1期)の国民所得(Yt+1)及び名目経済成長率を測定することも可能となる。
翌期(t+1期)の国民所得(Yt+1)=翌期首資本(国富)ストック(Kt+ΔKt)/βt
Where,
Kt: t期首の資本
ΔKt: t期の資本蓄積
Yt: t期の国民所得(償却後可処分所得)
βt: t期の資本/所得比率
特に、過剰債務が発生する場合には、その分、資本(国富)ベクトル がより毀損することとなるので、過剰債務控除後資本(国富)による翌期(t+1期)の国民所得(Yt+1)及び名目経済成長率を測定することも可能である。
[1] SNA(ストック編統合勘定)では、株式を「非金融資産」(=実体資産[real assets])ではなく、「持分・投資信託受益証券(Equity and Investment Fund Shares)」という「金融資産」として分類している。しかし、株式会社の発行する株式は当該株式会社の資本を構成するものであるから、株式保有者の立場から見れば、本来的には当該株式会社の負債に対応する金融資産には該当せず、むしろ非金融資産として分類すべきものである。
この記事が気に入ったらサポートをしてみませんか?
