行列の固有値問題を、多項方程式問題に帰着させて解いてみる。
行列の固有値問題は、フロベニウスの定理を介して(なのかはわかりませんが、、)、多項方程式の解問題に帰着させることができます。今回はこの性質を利用して、行列の固有値問題を解く方法を一つ提案として紹介してみようと思います。
手順①、行列による多項式が0になることを仮定して、逆行列を利用して係数を求める。
あるn行n列の正方行列Aが固有値$${λ_1、λ_2、λ_3、…}$$を持つ時、もしAの固有値が重複を含めてn個あることがわかっている場合は、
$${(A-λ_1 I)(A-λ_2 I)(A-λ_3 I)…=0}$$
と考えることができる(固有値に関しては一般的には0はとり得ないらしい。)。
この形は、行列を使った方程式であり、行列の固有値から一意に方程式の係数を決めることができるため、この係数を求めてみる。
$${a_1 A^n+a_2 A^{n-1}+ …+a_{n-1}A+I=0}$$(方程式①)
の形で表すことができる。(固有値に0がないことから、単位行列に0の係数がつく可能性は否定できます。)単位行列を右辺に移して、Aを行列ではなく変数としたときみたく、左辺から、ベクトル$${a=(a_0,a_1,…,a_{n-1})}$$(ベクトルa)を取って行列をまとめるならば、
$${\sum\limits_{k=1}^n a_{k-1}A^{n-k+1}B_k=-I}$$(方程式②)
ただし、B_kはn-k+1列のが項が全て1でその他の項が0となる行列とする。
と表すことができます。よって、最初にこの行列を計算して、逆行列を用いてベクトルaを求めれば、全ての係数を求めることができます。また、一通り説明が終わってから振り返りますが、Bの列をn以下の任意の数に減らすことができると思われるので、固有値をいくつかのサブの問題に分割して、並列して求めることができる可能性があると思われます。(以下pythonでの必要なプログラムを示します。)
(追記)ここで求めた係数は、コンパニオン行列(同伴行列)の係数にそのまま当てはめることができます。
a=np.eye(4)
b=np.zeros((4,4))
for i in range(4):
m=np.zeros((4,4))
a=a@n
m[:,3-i]=1
b=b+a@m
p=-b**-1@np.ones((4,1))手順②簡単な勾配法を用いて、できた方程式の根探索を行う。
簡単な勾配法を用いれば、方程式の解を順に求めることができます。今回使うのは、少し前に対角行列を用いてexcelで次数の多い方程式を解くためのツールを作った件を紹介しましたが、その時に使った方法を援用して説明します。
該当記事はこちら。
この記事で紹介しているツールについては、対角行列の左右に直行行列とその転置を作用させた場合に、できた行列の固有値は元の対角行列の固有値と変わらない性質を利用しています。
xによる方程式のxに、未知の変数を対角行列の対角成分として含む正方行列をそのまま代入して、定数部分を単位行列の積に置き換えた行列による式を考えた時、フロベニウスの定理により、できた行列の固有値は、元の行列の固有値をxの方程式のxに代入した値に等しくなります。代入する元の行列の固有値が方程式の解と全て一致している場合に限って、できた行列は全ての項が0の0行列となります。
今回は解の近似の仕方をだいぶ簡単にしています。重複する解同士が互いの解に収束するのを阻害する現象があり、これをexcelのGRG非線形のソルバーを使わずに解決する策を思いつかなかったからです。正直行列を使う必要もありません。ただ、ノルムからステップ幅の計算がやりやすかったことと、複数の解を同時に求めることにも応用が効くかもしれないことを期待して今回採用しました。
単位行列の係数を変数に選び単位行列にスカラー倍を作用させた行列を作る。その行列に、適当な直交行列を生成して左右に掛け算をします。結果できた行列をGとします。
求めたい多項式の係数と、Gの累乗とを互いに掛け算して、解を求めたい方程式に行列Gを代入した新しい行列(行列①)を作ります。
この行列のフロベニウスノルム(全ての要素の2乗和の平方根)をステップ幅にして、この行列の全ての項の足し算をした結果を実数、複素数方向の勾配方向として、順に勾配法で変数を更新していきます。
変数の正負が勾配方向と一致しないことがあるため、最初のステップの符号の変化を記憶した変数を毎回掛けておくことで、対応します。
勾配の方向は、行列①の全ての要素の総和を取り、その複素数を正規化して決めます。このように設定すると、値を更新するごとに行列①のフロベニウスノルムが縮小していきます。
フロベニウスノルムが0になるポイントでは、行列が0行列となり変数が行列の固有値に収束したと判断できます。こうやって固有値を一つ求めることができました。
r0=2
e=np.eye(r0)
for i in range(r0-1):
c=np.eye(r0)
c[i,i]=np.sin(1+i)
c[i,i+1]=np.cos(1+i)
c[1+i,i]=-np.cos(1+i)
c[1+i,1+i]=np.sin(1+i)
e=e@c
print(e)
f=np.zeros((r0,r0),dtype=np.complex)
f+=complex(3,0)*np.eye(r0)
g0=e@f@e.T
print(g0)
print(linalg.norm(e@f@e.T,"fro"))
g0res=np.eye(r0,dtype=complex)
d=np.eye(r0,dtype=complex)
for i in range(r-k):
d=d@g0
g0res+=p[r-1-k-i,0]*d
div0=np.ones((1,r0))@g0res@np.ones((r0,1))
norm=1
f+=complex(1,1)*np.eye(r0)
f0=f[0,0]
f1=1
j=0
while norm>1.0e-12 and j<1000:
j+=1
g=e@f@e.T
gres=np.eye(r0,dtype=complex)
d=np.eye(r0,dtype=complex)
for i in range(r-k):
d=d@g
gres+=p[r-1-k-i,0]*d
div=np.ones((1,r0))@(gres)@np.ones((r0,1))
norm=np.linalg.norm(gres,"fro")
kake=1
f0=f[0,0]
if norm<0.1:
kake=np.sqrt(norm)
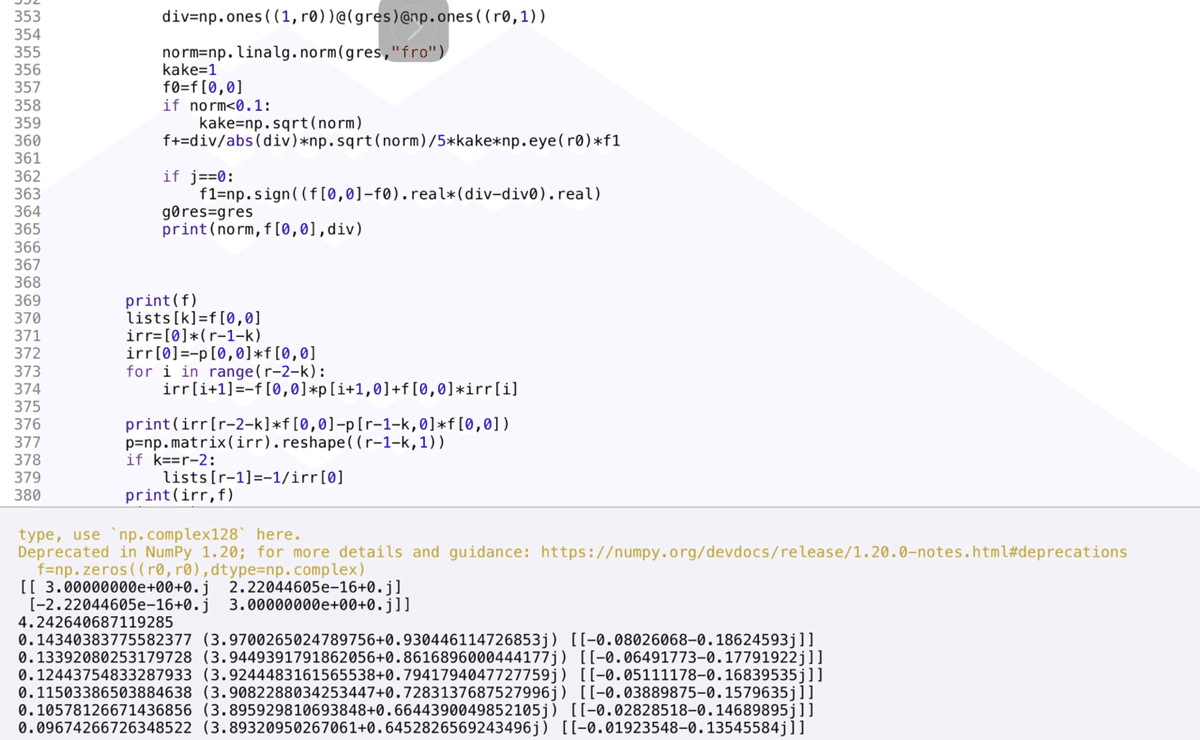
f+=div/abs(div)*np.sqrt(norm)/5*kake*np.eye(r0)*f1
if j==0:
f1=np.sign((f[0,0]-f0).real*(div-div0).real)
g0res=gres
手順③求めた解を使い、係数の次数を下げる。
求めた解で方程式①が割り切れることがわかっていれば、数値計算で方程式①を因数分解することができます。よって、新しく次数を下げた方程式①を定義し直すことができます。
$${(A-λ I)(a’_1 A^{n-1}+a’_2 A^{n-2}+ …+a’_{n-2}A+I)=0}$$(方程式①’)
係数については、$${a’_1=-λa_1,a’_k(k≧2)=λ(a’_{k-1}-a_k)}$$、最後の固有値は、最後から一つ手前の固有値を求めた時の、$${-\frac{1}{a’_1}}$$をそのまま最後の固有値として使えば答えが出揃います。
こうして、全ての固有値を求めることができるかと思います。

lists[k]=f[0,0]
irr=[0]*(r-1-k)
irr[0]=-p[0,0]*f[0,0]
for i in range(r-2-k):
irr[i+1]=-f[0,0]*p[i+1,0]+f[0,0]*irr[i]
print(irr[r-2-k]*f[0,0]-p[r-1-k,0]*f[0,0])
p=np.matrix(irr).reshape((r-1-k,1))
if k==r-2:
lists[r-1]=-1/irr[0]
print(irr,f)全コード
def roottansakudirect(gyouretu,rank):
nqueue=gyouretu
r=rank
lists=[0]*r
a=np.eye(r)
b=np.zeros((r,r))
for i in range(r):
m=np.zeros((r,r))
a=a@n
m[:,r-1-i]=1
b=b+a@m
p=-b**-1@np.ones((r,1))
r0=2
for k in range(r-1):
print(p)
e=np.eye(r0)
for i in range(r0-1):
c=np.eye(r0)
c[i,i]=np.sin(1+i)
c[i,i+1]=np.cos(1+i)
c[1+i,i]=-np.cos(1+i)
c[1+i,1+i]=np.sin(1+i)
e=e@c
print(e)
f=np.zeros((r0,r0),dtype=np.complex)
f+=complex(3,0)*np.eye(r0)
g0=e@f@e.T
print(g0)
print(linalg.norm(e@f@e.T,"fro"))
g0res=np.eye(r0,dtype=complex)
d=np.eye(r0,dtype=complex)
for i in range(r-k):
d=d@g0
g0res+=p[r-1-k-i,0]*d
div0=np.ones((1,r0))@g0res@np.ones((r0,1))
norm=1
f+=complex(1,1)*np.eye(r0)
f0=f[0,0]
f1=1
j=0
while norm>1.0e-12 and j<2000:
j+=1
g=e@f@e.T
gres=np.eye(r0,dtype=complex)
d=np.eye(r0,dtype=complex)
for i in range(r-k):
d=d@g
gres+=p[r-1-k-i,0]*d
div=np.ones((1,r0))@(gres)@np.ones((r0,1))
norm=np.linalg.norm(gres,"fro")
kake=1
f0=f[0,0]
if norm<0.1:
kake=np.sqrt(norm)
f+=div/abs(div)*np.sqrt(norm)/5*kake*np.eye(r0)*f1
if j==0:
f1=np.sign((f[0,0]-f0).real*(div-div0).real)
g0res=gres
print(norm,f[0,0],div)
print(f)
lists[k]=f[0,0]
irr=[0]*(r-1-k)
irr[0]=-p[0,0]*f[0,0]
for i in range(r-2-k):
irr[i+1]=-f[0,0]*p[i+1,0]+f[0,0]*irr[i]
print(irr[r-2-k]*f[0,0]-p[r-1-k,0]*f[0,0])
p=np.matrix(irr).reshape((r-1-k,1))
if k==r-2:
lists[r-1]=-1/irr[0]
print(irr,f)
print(lists)
return lists
roottansakudirect(n,4)
最後に並列化の可能性について
最後に、試してはいませんが、このコードで大きな行列の計算に対応する際に、固有値計算の問題をいくつかの小問題に切り分けて、並列化できる可能性について推測しているので話しておこうと思います。
nよりも低い次数で方程式①を組み立てたいと思った時に、方法がひとつあって、方程式②の行列Bについて、列をnよりも減らしてmにして、n行m列の行列Bとして計算すると、m個の係数で計算を進めることが可能です。
$${\sum\limits_{k=1}^{n} a_{k-1}A^{n-k+1}B_k=-I}$$(方程式③)
ただし、B_kはm-k+1列のが項が全て1でその他の項が0となる行列とする。
$${(a_1 A^{m-1}+a_2 A^{m-2}+ …+a_{m-2}A+I)=0}$$(方程式④)
この時の計算が逆行列を使った計算になるか、擬似逆行列を使わざるを得ないかはわかりませんが、擬似逆行列を使わずに計算できる場合は、固有値の一部をしっかりと求めることができるのかもしれない…と考えています。そのうち試してみようと思います。
この記事が気に入ったらサポートをしてみませんか?
